Hiperparametreler, eğitimin farklı yönlerini kontrol eden değişkenlerdir. Sık kullanılan üç hiperparametre şunlardır:
- Öğrenme oranı
- Grup boyutu
- Epochs (Dönemler)
Buna karşılık, parametreler, modelin kendisinde yer alan ağırlık ve önyargı gibi değişkenlerdir. Diğer bir deyişle, hiperparametreler sizin kontrol ettiğiniz değerlerdir. Parametreler ise modelin eğitim sırasında hesapladığı değerlerdir.
Öğrenme oranı
Öğrenme oranı, modeli ne kadar hızlı yakınlaştırdığınızı etkileyen, belirlediğiniz bir kayan nokta sayısıdır. Öğrenme oranı çok düşükse modelin yakınsaması uzun zaman alabilir. Ancak öğrenme oranı çok yüksekse model asla yakınsamaz, bunun yerine kaybı en aza indiren ağırlıklar ve sapma etrafında seker. Amaç, modelin hızlı bir şekilde yakınsaması için çok yüksek veya çok düşük olmayan bir öğrenme hızı seçmektir.
Öğrenme hızı, gradyan inişi sürecinin her adımında ağırlıklarda ve yanlılıkta yapılacak değişikliklerin büyüklüğünü belirler. Model, bir sonraki yineleme için modelin parametrelerini (ağırlık ve sapma değerleri) belirlemek üzere gradyanı öğrenme hızıyla çarpar. Gradyan inişinin üçüncü adımında, negatif eğim yönünde hareket etmek için kullanılan "küçük miktar" öğrenme hızını ifade eder.
Eski model parametreleri ile yeni model parametreleri arasındaki fark, kayıp fonksiyonunun eğimiyle orantılıdır. Örneğin, eğim büyükse model büyük bir adım atar. Küçükse küçük bir adım atar. Örneğin, gradyanın büyüklüğü 2,5 ve öğrenme oranı 0,01 ise model, parametreyi 0,025 oranında değiştirir.
İdeal öğrenme hızı, modelin makul sayıda yineleme içinde yakınlaşmasına yardımcı olur. Şekil 20'de, kayıp eğrisi, modelin yakınsamaya başlamadan önce ilk 20 yineleme sırasında önemli ölçüde iyileştiğini gösteriyor:
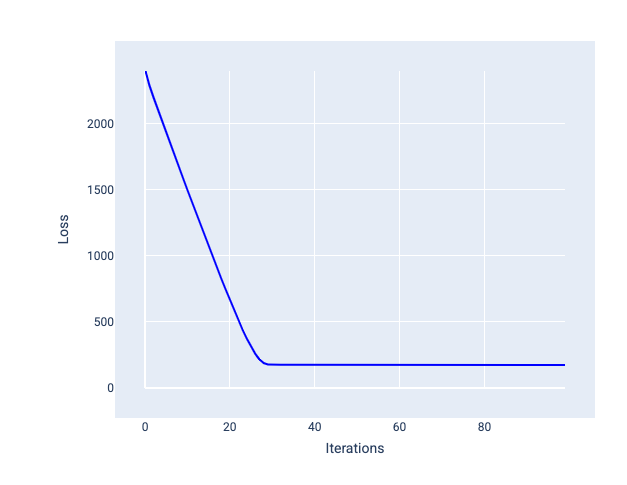
Şekil 20. Hızlı yakınsayan bir öğrenme hızıyla eğitilmiş modeli gösteren kayıp grafiği.
Buna karşılık, çok küçük bir öğrenme hızı, yakınsama için çok fazla yineleme gerektirebilir. Şekil 21'de, kayıp eğrisi modelin her iterasyondan sonra yalnızca küçük iyileştirmeler yaptığını gösteriyor:
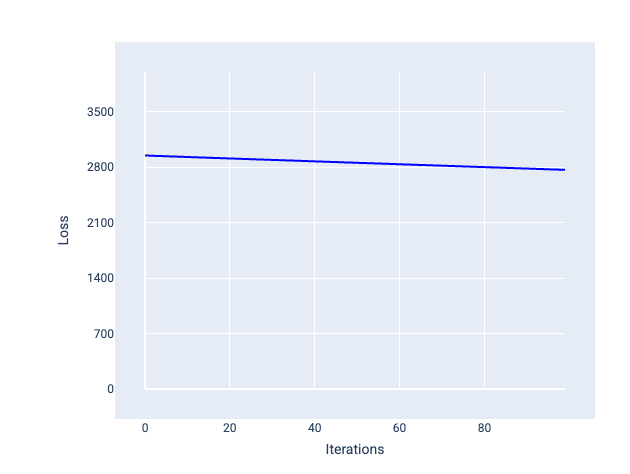
Şekil 21. Küçük bir öğrenme hızıyla eğitilmiş modeli gösteren kayıp grafiği.
Çok yüksek bir öğrenme hızı, her iterasyon kaybın dalgalanmasına veya sürekli artmasına neden olduğundan asla yakınsamaz. Şekil 22'de, kayıp eğrisi modelin her yinelemeden sonra kaybı azaltıp artırdığını gösteriyor. Şekil 23'te ise kayıp sonraki yinelemelerde artıyor:
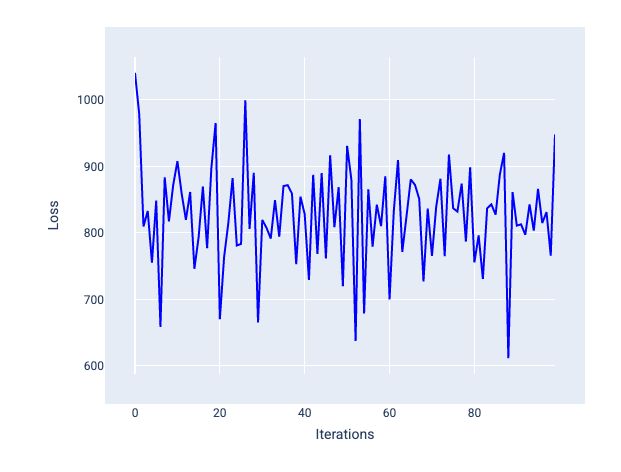
Şekil 22. Kayıp eğrisinin yinelemeler arttıkça yukarı ve aşağı hareket ederek çok fazla dalgalandığı, çok büyük bir öğrenme hızıyla eğitilmiş bir modeli gösteren kayıp grafiği.
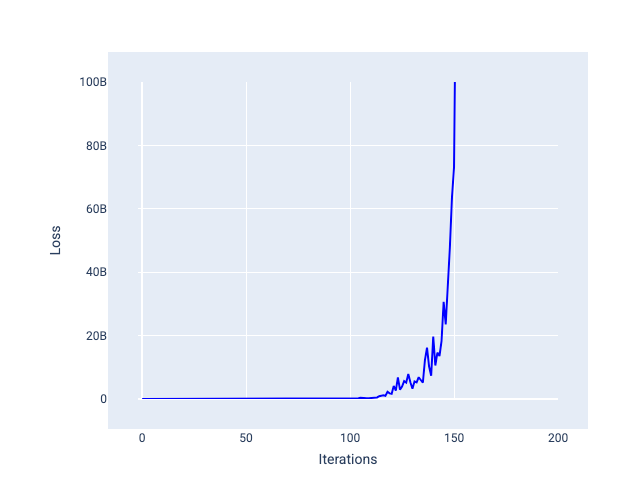
Şekil 23. Öğrenme hızı çok yüksek olan bir modelin eğitildiği ve sonraki yinelemelerde kayıp eğrisinin önemli ölçüde arttığı kayıp grafiği.
Alıştırma: Anlayıp anlamadığınızı kontrol edin
Grup boyutu
Toplu iş boyutu, modelin ağırlıklarını ve önyargısını güncellemeden önce işlediği örneklerin sayısını ifade eden bir hiperparametredir. Ağırlıkları ve önyargıyı güncellemeden önce modelin veri kümesindeki her örnek için kaybı hesaplaması gerektiğini düşünebilirsiniz. Ancak bir veri kümesi yüz binlerce hatta milyonlarca örnek içerdiğinde tam grubu kullanmak pratik değildir.
Ağırlıkları ve önyargıyı güncellemeden önce veri kümesindeki her örneğe bakmaya gerek kalmadan ortalama üzerinde doğru gradyanı elde etmek için kullanılan iki yaygın teknik şunlardır: Stokastik gradyan inişi ve mini toplu stokastik gradyan inişi.
Stokastik gradyan inişi (SGD): Stokastik gradyan inişi, yineleme başına yalnızca tek bir örnek (bir toplu iş boyutu) kullanır. Yeterli sayıda yineleme yapıldığında SGD çalışır ancak çok gürültülüdür. "Gürültü", eğitim sırasında yineleme esnasında kaybın azalmak yerine artmasına neden olan varyasyonları ifade eder. "Stokastik" terimi, her grubu oluşturan bir örneğin rastgele seçildiğini gösterir.
Aşağıdaki resimde, model ağırlıklarını ve önyargısını SGD kullanarak güncellediği için kaybın nasıl biraz dalgalandığına dikkat edin. Bu durum, kayıp grafiğinde gürültüye yol açabilir:
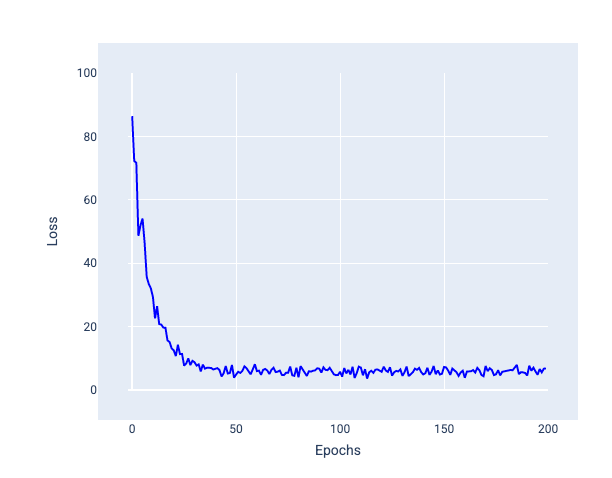
Şekil 24. Kayıp eğrisinde gürültü gösteren stokastik gradyan inişi (SGD) ile eğitilmiş model.
Stokastik gradyan inişinin, yalnızca yakınsama noktasında değil, tüm kayıp eğrisinde gürültü oluşturabileceğini unutmayın.
Mini toplu stokastik gradyan inişi (mini toplu SGD): Mini toplu stokastik gradyan inişi, tam toplu ve SGD arasında bir uzlaşmadır. $ N $ sayıda veri noktası için toplu iş boyutu 1'den büyük ve $ N $ değerinden küçük herhangi bir sayı olabilir. Model, her toplu işe dahil edilen örnekleri rastgele seçer, gradyanlarını ortalamasını alır ve ardından ağırlıkları ve yanlılığı yineleme başına bir kez günceller.
Her bir toplu iş için örnek sayısını belirleme işlemi, veri kümesine ve kullanılabilir bilgi işlem kaynaklarına bağlıdır. Genel olarak, küçük toplu iş boyutları SGD gibi davranır ve daha büyük toplu iş boyutları tam toplu iş gradyan inişi gibi davranır.
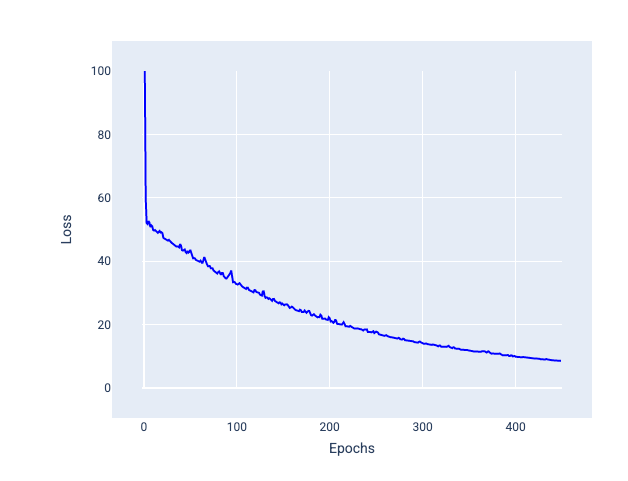
Şekil 25. Mini toplu SGD ile eğitilmiş model.
Bir modeli eğitirken gürültünün ortadan kaldırılması gereken istenmeyen bir özellik olduğunu düşünebilirsiniz. Ancak belirli bir miktarda gürültü faydalı olabilir. İlerleyen modüllerde, gürültünün bir modelin daha iyi genelleme yapmasına ve bir sinir ağında optimum ağırlıkları ve önyargıyı bulmasına nasıl yardımcı olabileceğini öğreneceksiniz.
Epochs
Eğitim sırasında dönem, modelin eğitim setindeki her örneği bir kez işlediği anlamına gelir. Örneğin, 1.000 örnek içeren bir eğitim kümesi ve 100 örnek içeren bir mini toplu iş boyutu verildiğinde, modelin bir dönemi tamamlaması 10 iterasyon sürer.
Eğitim genellikle birçok dönem gerektirir. Yani sistemin, eğitim setindeki her örneği birden çok kez işlemesi gerekir.
Dönem sayısı, model eğitime başlamadan önce ayarladığınız bir hiperparametredir. Çoğu durumda, modelin yakınsaması için kaç dönem gerektiği konusunda denemeler yapmanız gerekir. Genel olarak, daha fazla dönem daha iyi bir model oluşturur ancak eğitilmesi daha uzun sürer.
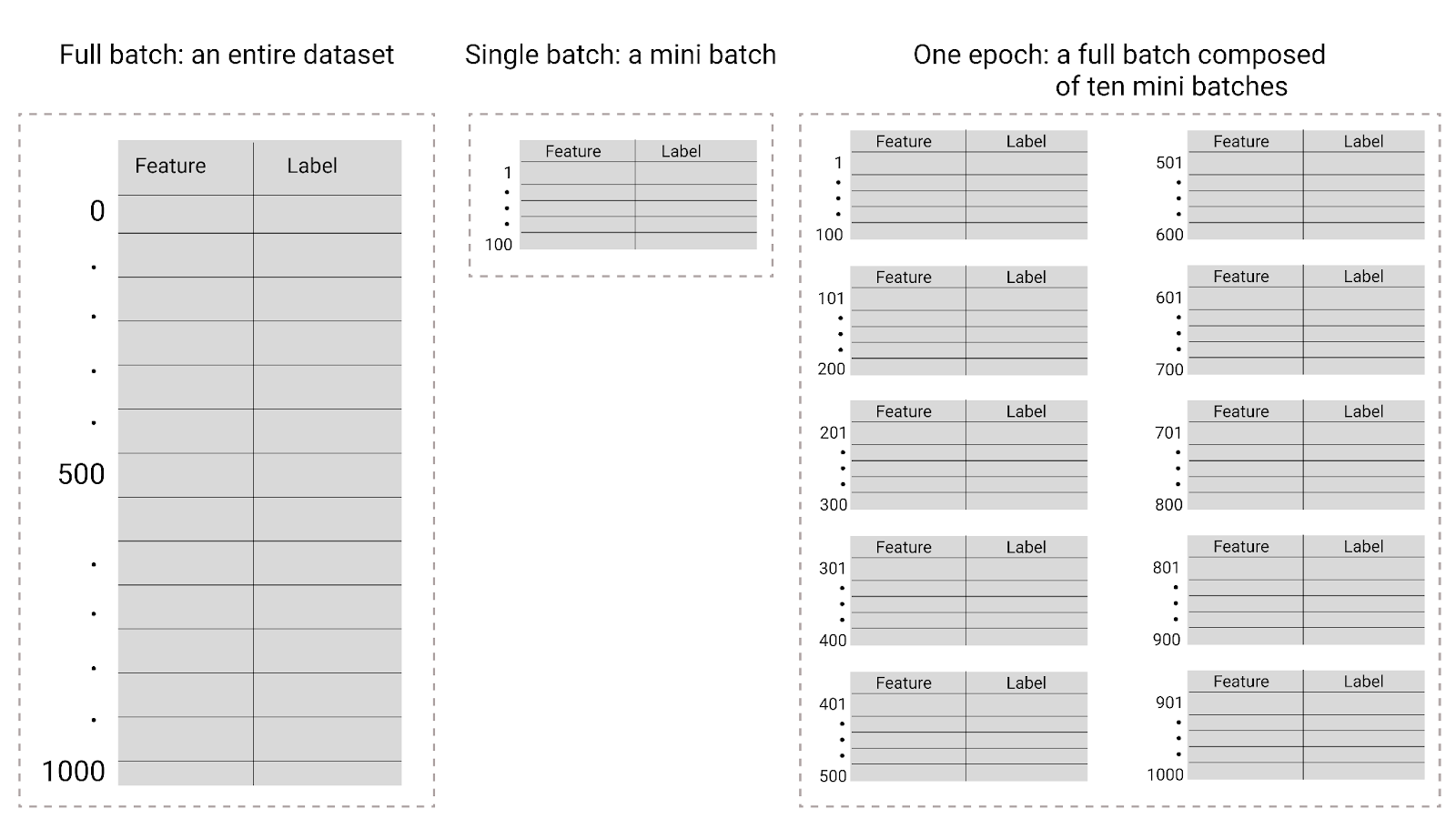
Şekil 26. Tam toplu işleme ve mini toplu işleme karşılaştırması.
Aşağıdaki tabloda, toplu iş boyutu ve dönemlerin, bir modelin parametrelerini güncelleme sayısı ile nasıl ilişkili olduğu açıklanmaktadır.
| Toplu işlem türü | Ağırlık ve önyargı güncellemeleri gerçekleştiğinde |
|---|---|
| Tam toplu iş | Model, veri kümesindeki tüm örneklere baktıktan sonra. Örneğin, bir veri kümesi 1.000 örnek içeriyorsa ve model 20 dönem boyunca eğitiliyorsa model, ağırlıkları ve yanlılığı dönem başına bir kez olmak üzere 20 kez günceller. |
| Stokastik gradyan inişi | Model, veri kümesindeki tek bir örneği inceledikten sonra. Örneğin, bir veri kümesi 1.000 örnek içeriyorsa ve 20 dönem boyunca eğitiliyorsa model, ağırlıkları ve yanlılığı 20.000 kez günceller. |
| Mini toplu stokastik gradyan inişi | Model, her gruptaki örneklere baktıktan sonra. Örneğin, bir veri kümesi 1.000 örnek içeriyorsa, toplu iş boyutu 100 ise ve model 20 dönem boyunca eğitiliyorsa model, ağırlıkları ve yanlılığı 200 kez günceller. |