Gli iperparametri sono variabili che controllano diversi aspetti dell'addestramento. Tre iperparametri comuni sono:
I parametri, invece, sono le variabili, come i pesi e la bias, che fanno parte del modello stesso. In altre parole, gli iperparametri sono valori che puoi controllare; i parametri sono valori che il modello calcola durante l'addestramento.
Tasso di apprendimento
Il tasso di apprendimento è un numero in virgola mobile impostato che influisce sulla velocità di convergenza del modello. Se il tasso di apprendimento è troppo basso, il modello può richiedere molto tempo per convergere. Tuttavia, se il tasso di apprendimento è troppo elevato, il modello non converge mai, ma oscilla intorno ai pesi e ai bias che riducono al minimo la perdita. L'obiettivo è scegliere un tasso di apprendimento non troppo alto né troppo basso in modo che il modello converi rapidamente.
Il tasso di apprendimento determina l'entità delle modifiche da apportare alle ponderazioni e ai bias durante ogni fase del processo di discesa del gradiente. Il modello moltiplica la derivata per il tasso di apprendimento per determinare i parametri del modello (valori di bias e ponderazione) per l'iterazione successiva. Nel terzo passaggio della discesa del gradiente, la "quantità ridotta" da spostare nella direzione del declivio negativo si riferisce al tasso di apprendimento.
La differenza tra i parametri del vecchio modello e quelli del nuovo è proporzionale alla pendenza della funzione di perdita. Ad esempio, se la pendenza è elevata, il modello fa un passo grande. Se è piccolo, è sufficiente un piccolo passo. Ad esempio, se l'intensità del gradiente è 2,5 e il tasso di apprendimento è 0,01, il modello modificherà il parametro di 0,025.
Il tasso di apprendimento ideale aiuta il modello a convergere entro un numero ragionevole di iterazioni. Nella Figura 21, la curva di perdita mostra il miglioramento significativo del modello durante le prime 20 iterazioni prima di iniziare a convergere:
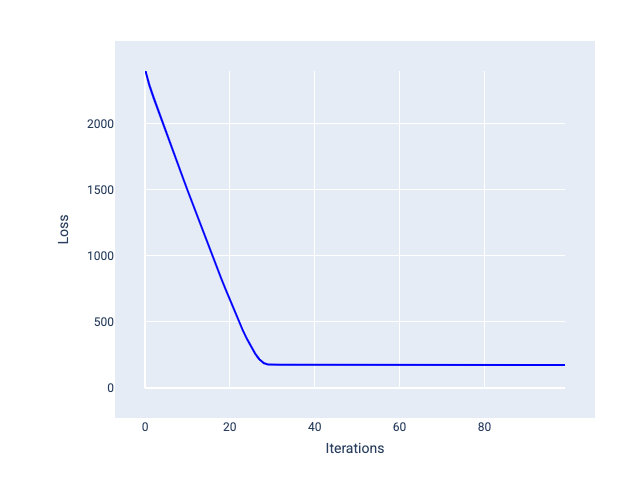
Figura 21. Grafico della perdita che mostra un modello addestrato con una frequenza di apprendimento che converrebbe rapidamente.
Al contrario, un tasso di apprendimento troppo basso può richiedere troppe iterazioni per convergere. Nella Figura 22, la curva di perdita mostra che il modello apporta solo miglioramenti minimi dopo ogni iterazione:
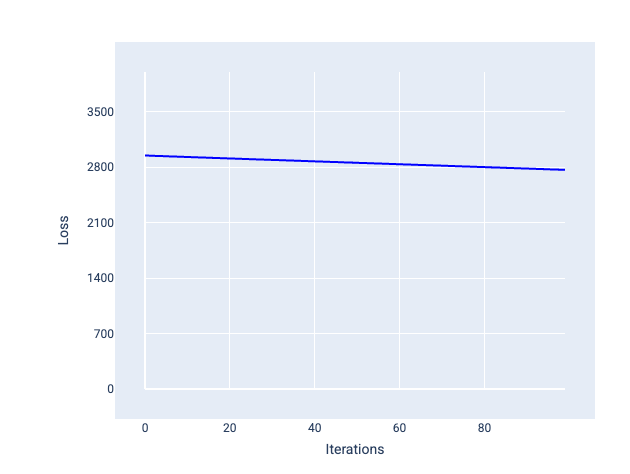
Figura 22. Grafico di perdita che mostra un modello addestrato con un piccolo tasso di apprendimento.
Un tasso di apprendimento troppo elevato non converge mai perché ogni iterazione provoca una perdita di rimbalzo o un aumento continuo. Nella Figura 23, la curva di perdita mostra la perdita del modello che diminuisce e poi aumenta dopo ogni iterazione, mentre nella Figura 24 la perdita aumenta nelle iterazioni successive:
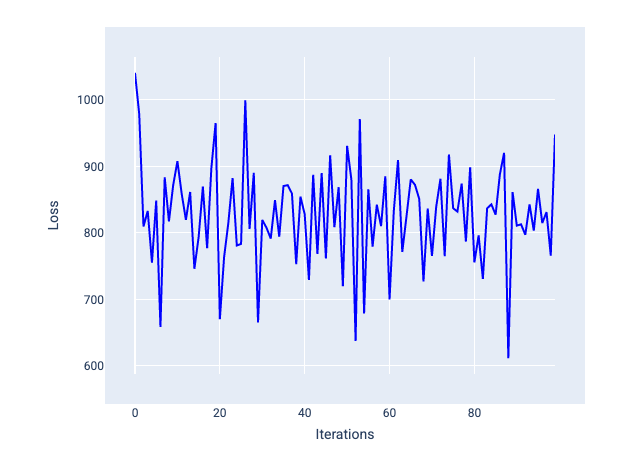
Figura 23. Grafico di perdita che mostra un modello addestrato con un tasso di apprendimento troppo elevato, in cui la curva di perdita oscilla notevolmente, salendo e scendendo con l'aumento delle iterazioni.
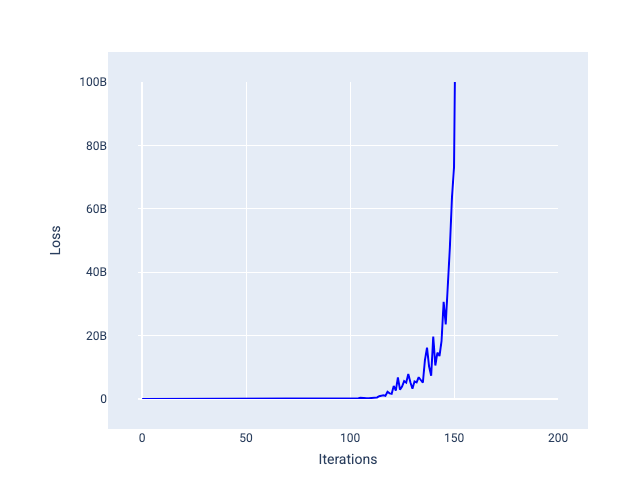
Figura 24. Grafico della perdita che mostra un modello addestrato con un tasso di apprendimento troppo elevato, in cui la curva di perdita aumenta drasticamente nelle iterazioni successive.
Esercizio: verifica la tua comprensione
Dimensione del batch
La dimensione del batch è un iperparametro che fa riferimento al numero di esempi elaborati dal modello prima di aggiornarne le ponderazioni e i bias. Potresti pensare che il modello debba calcolare la perdita per ogni esempio nel set di dati prima di aggiornare i pesi e la bias. Tuttavia, quando un insieme di dati contiene centinaia di migliaia o addirittura milioni di esempi, l'utilizzo del lotto completo non è pratico.
Due tecniche comuni per ottenere il gradiente giusto in media senza dover esaminare ogni esempio nel set di dati prima di aggiornare i pesi e i bias sono la discesa stocastica del gradiente e la discesa stocastica del gradiente in mini-batch:
Discesa stocastica del gradiente (SGD): la discesa stocastica del gradiente utilizza solo un singolo esempio (un batch di dimensione 1) per ogni iterazione. Dopo un numero sufficiente di iterazioni, la SGD funziona, ma è molto rumorosa. Per "rumore" si intendono le variazioni durante l'addestramento che causano un aumento della perdita anziché una sua diminuzione durante un iterazione. Il termine "stocastico" indica che l'unico esempio che compone ogni batch viene scelto in modo casuale.
Nell'immagine seguente, nota come la perdita fluttua leggermente man mano che il modello aggiorna i suoi pesi e bias utilizzando l'SGD, il che può portare a rumore nel grafico della perdita:
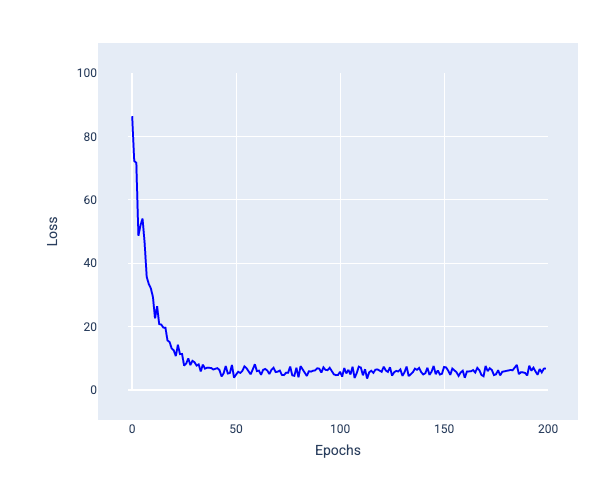
Figura 25. Modello addestrato con discesa stocastica del gradiente (SGD) che mostra il rumore nella curva di perdita.
Tieni presente che l'utilizzo della discesa del gradiente stocastico può produrre rumore nell'intera curva di perdita, non solo in prossimità della convergenza.
Discesa stocastica del gradiente in mini-batch (SGD mini-batch): la discesa stocastica del gradiente in mini-batch è un compromesso tra full-batch e SGD. Per un numero di punti dati $ N $, la dimensione del batch può essere un numero qualsiasi maggiore di 1 e minore di $ N $. Il modello sceglie gli esempi inclusi in ogni batch in modo casuale, ne calcola la media dei gradienti e poi aggiorna i pesi e la bias una volta per iterazione.
La determinazione del numero di esempi per ogni batch dipende dal set di dati e dalle risorse di calcolo disponibili. In generale, i batch di piccole dimensioni si comportano come la SGD, mentre i batch di dimensioni maggiori si comportano come la discesa del gradiente con batch completo.
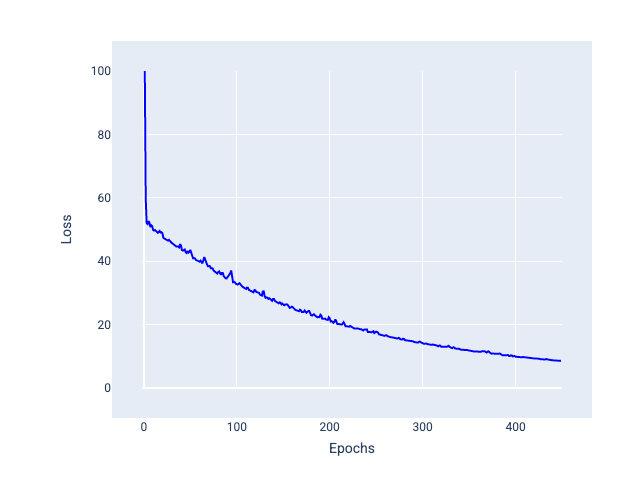
Figura 26. Modello addestrato con SGD con mini-batch.
Quando addestrini un modello, potresti pensare che il rumore sia una caratteristica sgradevole da eliminare. Tuttavia, un certo livello di rumore può essere positivo. Nei moduli successivi, scoprirai in che modo il rumore può aiutare un modello a generalizzarsi meglio e a trovare i pesi e i bias ottimali in una rete neurale.
Epoche
Durante l'addestramento, un periodo indica che il modello ha elaborato ogni esempio nel set di addestramento una volta. Ad esempio, dato un set di addestramento con 1000 esempi e una dimensione del mini-batch di 100 esempi, il modello impiegherà 10 iterations per completare un periodo.
L'addestramento richiede in genere molte epoche. In altre parole, il sistema deve elaborare ogni esempio del set di addestramento più volte.
Il numero di epoche è un iperparametro che imposti prima dell'inizio dell'addestramento del modello. In molti casi, dovrai fare esperimenti per capire quante epoche sono necessarie per la convergenza del modello. In generale, un maggior numero di epoche produce un modello migliore, ma richiede anche più tempo per l'addestramento.
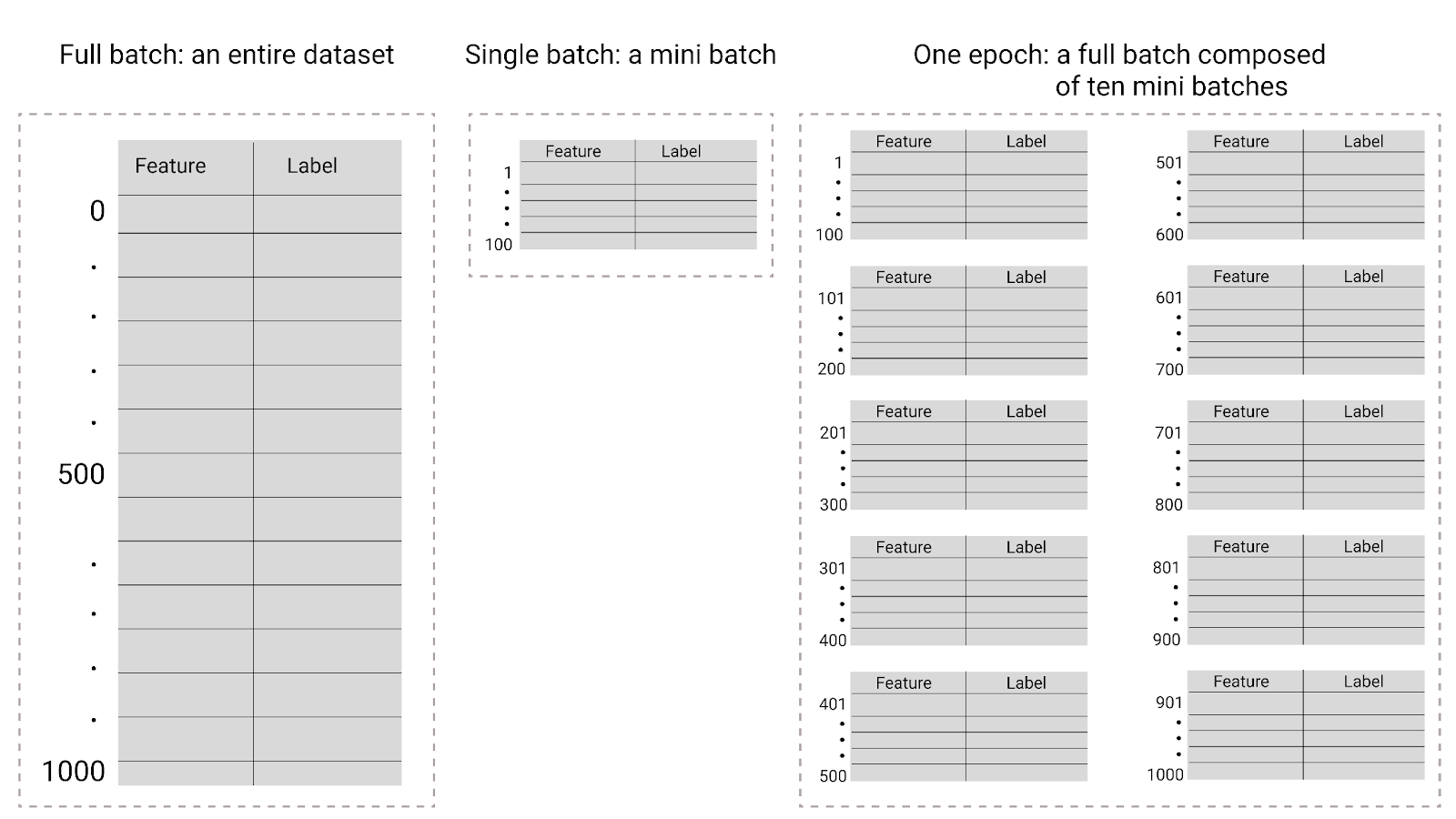
Figura 27. Batch completo rispetto al mini-batch.
La seguente tabella descrive la relazione tra dimensione del batch ed epoche e il numero di volte in cui un modello aggiorna i propri parametri.
| Tipo batch | Quando si verificano aggiornamenti di pesi e bias |
|---|---|
| Batch completo | Dopo che il modello ha esaminato tutti gli esempi nel set di dati. Ad esempio, se un set di dati contiene 1000 esempi e il modello viene addestrato per 20 epoche, il modello aggiorna i pesi e il bias 20 volte, una volta per epoca. |
| Discesa stocastica del gradiente | Dopo che il modello ha esaminato un singolo esempio del set di dati. Ad esempio, se un set di dati contiene 1000 esempi e viene addestrato per 20 epoche, il modello aggiorna i pesi e il bias 20.000 volte. |
| Discesa stocastica del gradiente in mini-batch | Dopo che il modello ha esaminato gli esempi in ogni batch. Ad esempio, se un set di dati contiene 1000 esempi, la dimensione del batch è 100 e il modello viene addestrato per 20 epoche, il modello aggiorna i pesi e la bias 200 volte. |