Les hyperparamètres sont des variables. qui contrôlent différents aspects de l'entraînement. Voici trois hyperparamètres courants:
Les paramètres, en revanche, variables, comme les pondérations et les biais, qui font partie du modèle. Dans Autrement dit, les hyperparamètres sont des valeurs que vous contrôlez ; les paramètres sont des valeurs que le modèle calcule lors de l'entraînement.
Taux d'apprentissage
Le taux d'apprentissage est un nombre à virgule flottante que vous définissez, qui influence la vitesse à laquelle le modèle converge. Si le taux d'apprentissage est trop faible, le modèle peut prendre beaucoup de temps de converger. Toutefois, si le taux d'apprentissage est trop élevé, converge, mais rebondit autour des pondérations et des biais qui minimisent de perte de données. L'objectif est de choisir un taux d'apprentissage ni trop élevé, ni trop faible. que le modèle converge rapidement.
Le taux d'apprentissage détermine l'amplitude des modifications à apporter aux pondérations et les biais à chaque étape du processus de descente de gradient. Le modèle multiplie le gradient par le taux d'apprentissage pour déterminer les paramètres du modèle (pondération et les valeurs de biais) pour la prochaine itération. Lors de la troisième étape du gradient descent, la "petite quantité" pour aller dans la direction de pente négative fait référence au taux d'apprentissage.
La différence entre les paramètres de l'ancien modèle et du nouveau est proportionnelle à la pente de la fonction de perte. Par exemple, si la pente est le modèle prend un grand pas. S'il est petit, il faut un petit pas. Pour exemple : si la magnitude du gradient est de 2,5 et que le taux d'apprentissage est de 0,01, alors le modèle modifie le paramètre de 0,025.
Le taux d'apprentissage idéal aide le modèle à converger dans un nombre raisonnable d'itérations. Dans la figure 21, la courbe de fonction de perte montre le modèle de manière significative s'améliorent au cours des 20 premières itérations avant que la convergence ne commence:
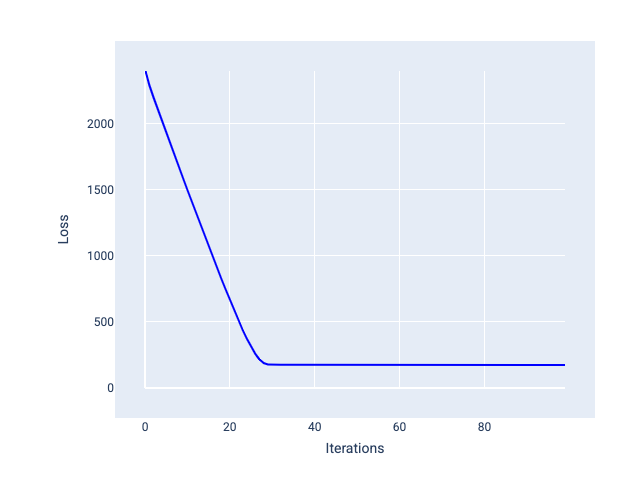
Figure 21 : Graphique de perte représentant un modèle entraîné avec un taux d'apprentissage converge rapidement.
En revanche, un taux d'apprentissage trop faible peut nécessiter trop d'itérations converger. Dans la figure 22, la courbe de fonction de perte montre que le modèle ne génère après chaque itération:
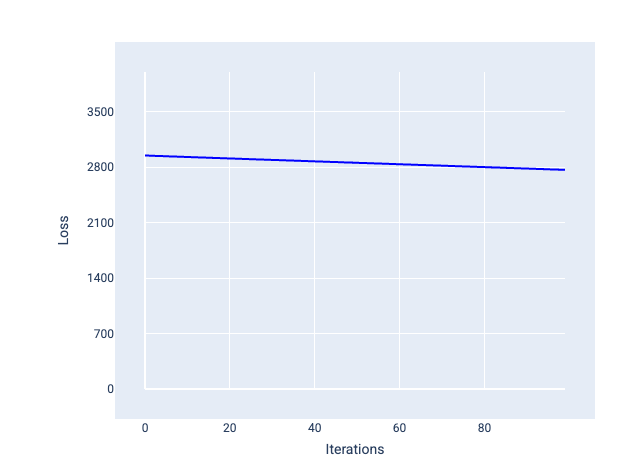
Figure 22 : Graphique de perte illustrant un modèle entraîné avec un taux d'apprentissage faible.
Un taux d'apprentissage trop élevé ne converge jamais, car chaque itération la perte rebondit ou augmente continuellement. Dans la figure 23, la perte montre que le modèle diminue, puis augmente la perte après chaque itération. Dans la figure 24, la perte augmente lors des itérations suivantes:
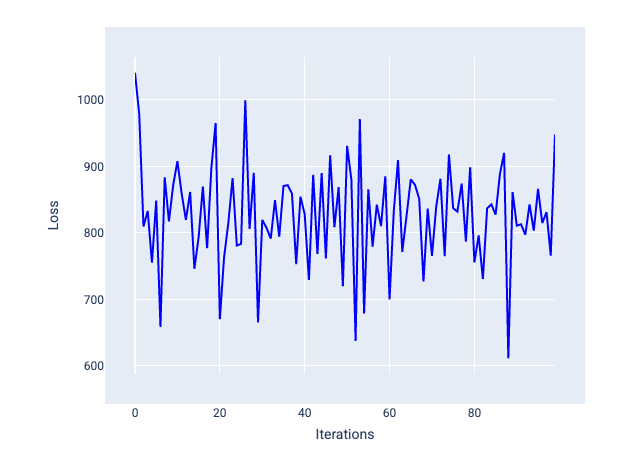
Figure 23 : Graphique de perte représentant un modèle entraîné avec un taux d'apprentissage trop grande, où la courbe de fonction de perte fluctue énormément, de haut en bas du nombre d'itérations.
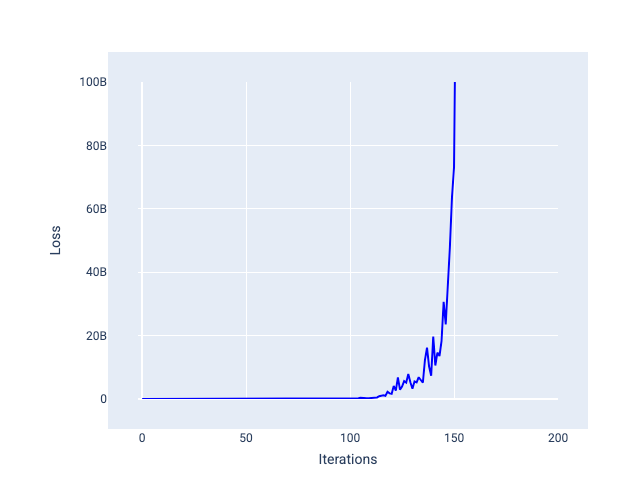
Figure 24 : Graphique de perte représentant un modèle entraîné avec un taux d'apprentissage trop grande, où la courbe de fonction de perte augmente considérablement dans les itérations suivantes.
Exercice: tester vos connaissances
Taille de lot
La taille de lot est un hyperparamètre qui fait référence au nombre d'exemples traités par le modèle avant de mettre à jour ses pondérations et des biais. Vous pourriez penser que le modèle doit calculer la perte pour chaque dans l'ensemble de données avant de mettre à jour les pondérations et les biais. Toutefois, lorsqu'un contient des centaines de milliers, voire des millions d'exemples, un lot complet n'est pas pratique.
Deux techniques courantes permettant d'obtenir le bon gradient en moyenne sans avoir à examiner chaque exemple de l'ensemble de données avant de mettre à jour les pondérations et les biais descente de gradient stochastique et gradient stochastique par mini-lots descent:
Descente de gradient stochastique (SGD): la descente de gradient stochastique n'utilise un seul exemple (une taille de lot d'un) par itération. Assez données des itérations, la SGD fonctionne, mais comporte beaucoup de bruit. "Bruit" fait référence aux variations pendant entraînant une augmentation plutôt qu'une diminution de la perte l'itération. Le terme "stochastique" indique que l'exemple comprenant chaque lot est choisi au hasard.
Dans l'image suivante, vous remarquerez que la perte fluctue légèrement selon le modèle. met à jour ses pondérations et ses biais à l'aide de la SGD, ce qui peut entraîner du bruit dans la perte graphique:
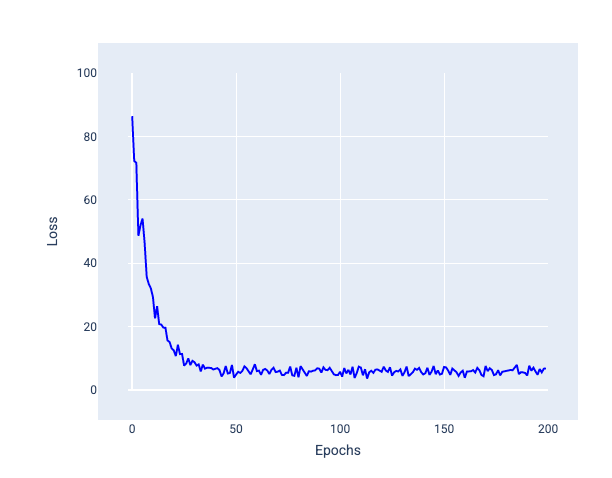
Figure 25 : Le modèle entraîné avec une descente de gradient stochastique (SGD) indique du bruit dans la courbe de fonction de perte.
Notez que la descente de gradient stochastique peut produire du bruit dans l'ensemble la courbe de fonction de perte, et pas seulement un phénomène proche de la convergence.
Descente de gradient stochastique par mini-lots (SGD par mini-lot): mini-lot la descente de gradient stochastique est un compromis entre les lots complets et la SGD. Pour $ N $ nombre de points de données, la taille de lot peut être n'importe quel nombre supérieur à 1 et inférieure à $ N $. Le modèle choisit les exemples inclus dans chaque lot fait la moyenne de leurs gradients, puis met à jour les pondérations et le biais une fois par itération.
La détermination du nombre d'exemples pour chaque lot dépend de l'ensemble de données et les ressources de calcul disponibles. En général, les petites tailles de lot se comportent comme SGD et des tailles de lot plus importantes se comportent comme une descente de gradient par lot complet.
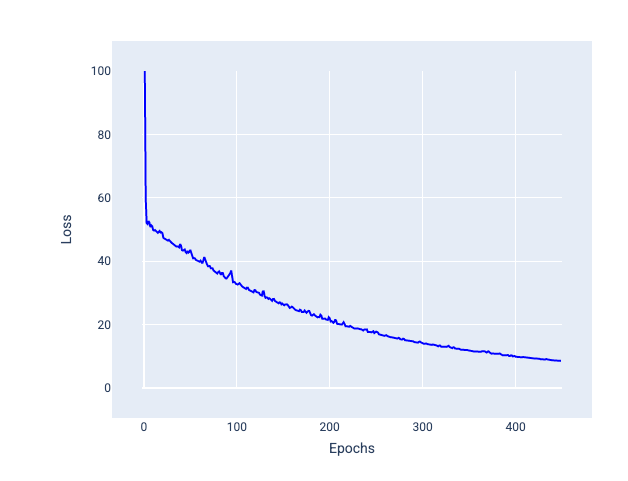
Figure 26 : Modèle entraîné avec des SGD par mini-lots.
Lorsque vous entraînez un modèle, vous pouvez penser que le bruit n'est pas souhaitable qui doit être éliminée. Cependant, une certaine quantité de bruit peut soit une bonne chose. Dans les modules suivants, vous découvrirez comment le bruit peut aider un modèle généraliser plus facilement et trouver des pondérations et des biais optimaux dans un neural réseau.
Époques
Pendant l'entraînement, une epoch signifie que a traité chaque exemple de l'ensemble d'entraînement une fois. Par exemple, pour un ensemble d'entraînement de 1 000 exemples et une taille de mini-lot de 100 exemples, le modèle effectue 10 itérations pour pour terminer une époque.
L'entraînement nécessite généralement de nombreuses époques. Autrement dit, le système doit traiter chaque exemple de l'ensemble d'entraînement.
Le nombre d'époques est un hyperparamètre que vous définissez avant le début du modèle de machine learning. Dans de nombreux cas, vous devez tester le nombre d'époques pour que le modèle converge. En général, plus le nombre d'époques est important, plus le modèle est meilleur, mais l'entraînement prend également plus de temps.
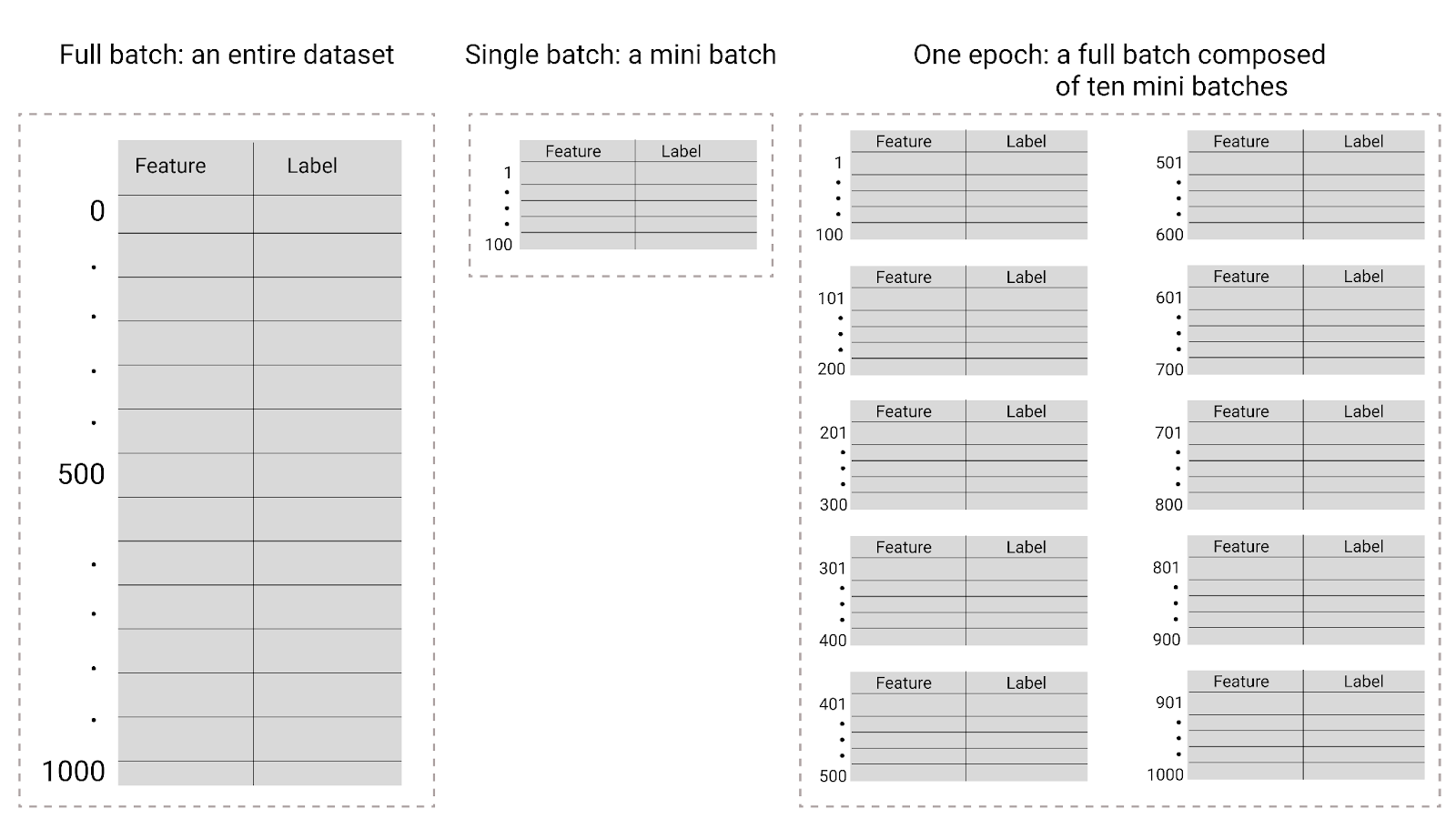
Figure 27 : Lot complet ou mini-lot.
Le tableau suivant décrit le lien entre la taille de lot et les époques par rapport au nombre Nombre de fois où un modèle met à jour ses paramètres.
| Type de lot | En cas de mises à jour des pondérations et des biais |
|---|---|
| Lot complet | Une fois que le modèle a examiné tous les exemples de l'ensemble de données, Par exemple, Si un ensemble de données contient 1 000 exemples et que le modèle est entraîné pour 20 époques, le modèle met à jour les pondérations et le biais 20 fois, une fois par époque. |
| Descente de gradient stochastique | Après que le modèle a examiné un seul exemple de l'ensemble de données Par exemple, si un ensemble de données contient 1 000 exemples et s'entraîne 20 époques, le modèle met à jour les pondérations et le biais 20 000 fois. |
| Descente de gradient stochastique par mini-lot | Une fois que le modèle a examiné les exemples de chaque lot. Par exemple, si un ensemble de données contient 1 000 exemples et que la taille de lot est de 100 ; le modèle est entraîné pour 20 époques, il met à jour les pondérations biaisées 200 fois. |