ハイパーパラメータは、トレーニングのさまざまな側面を制御する変数です。一般的なハイパーパラメータは次の 3 つです。
一方、パラメータは、重みやバイアスなど、モデル自体の一部である変数です。つまり、ハイパーパラメータはユーザーが制御する値であり、パラメータはトレーニング中にモデルが計算する値です。
学習率
学習率は、モデルの収束速度に影響する浮動小数点数です。学習率が低すぎると、モデルの収束に時間がかかることがあります。ただし、学習率が高すぎると、モデルは収束せず、損失を最小限に抑える重みとバイアスを飛び回ります。目標は、モデルが迅速に収束するように、高すぎず低すぎない学習率を選択することです。
学習率は、勾配降下法の各ステップで重みとバイアスに加える変更の大きさを決定します。モデルは、勾配に学習率を掛けて、次のイテレーションのモデルのパラメータ(重みとバイアスの値)を決定します。勾配降下法のステップ 3 で、負の傾斜方向に移動する「少量」は学習率を指します。
古いモデル パラメータと新しいモデル パラメータの差は、損失関数の傾きに比例します。たとえば、傾きが大きい場合、モデルは大きなステップを実行します。小さい場合は、小さなステップで実行されます。たとえば、グラデーションの大きさが 2.5 で学習率が 0.01 の場合、モデルはパラメータを 0.025 変更します。
最適な学習率は、モデルが妥当な反復回数で収束するのに役立ちます。図 20 の損失曲線は、モデルが最初の 20 回のイテレーションで大幅に改善され、その後収束し始めることを示しています。
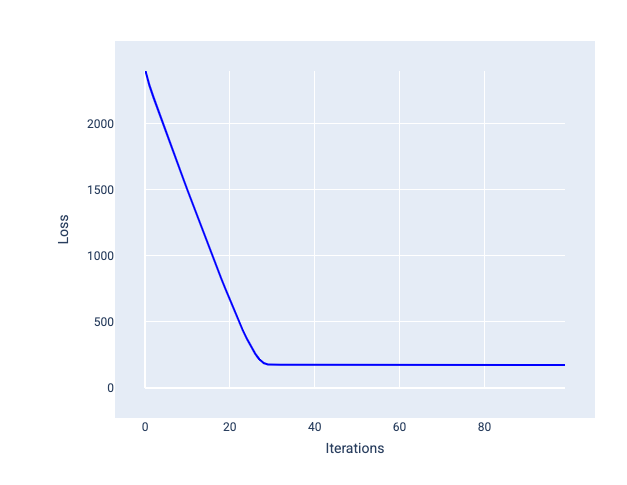
図 20. 学習率が速く収束するモデルでトレーニングされた損失グラフ。
一方、学習率が小さすぎると、収束に多くの反復が必要になる可能性があります。図 21 の損失曲線は、モデルが各反復処理後にわずかな改善しか行っていないことを示しています。
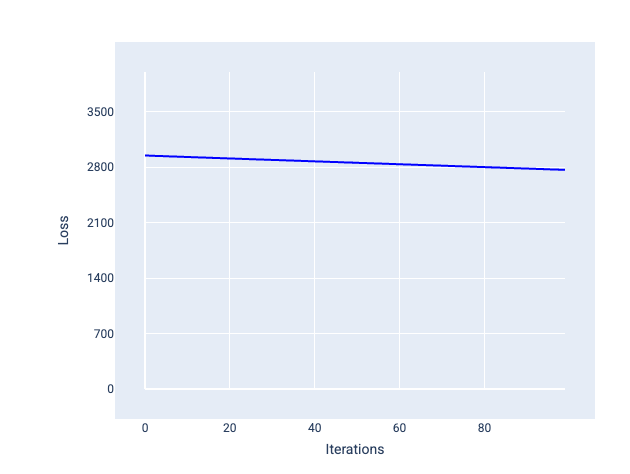
図 21. 学習率が小さいモデルのトレーニング損失を示すグラフ。
学習率が大きすぎると、各イテレーションで損失が大きく変動するか、継続的に増加するため、収束しません。図 22 の損失曲線は、モデルが各イテレーションの後に損失を減らし、その後増加することを示しています。図 23 では、後のイテレーションで損失が増加しています。
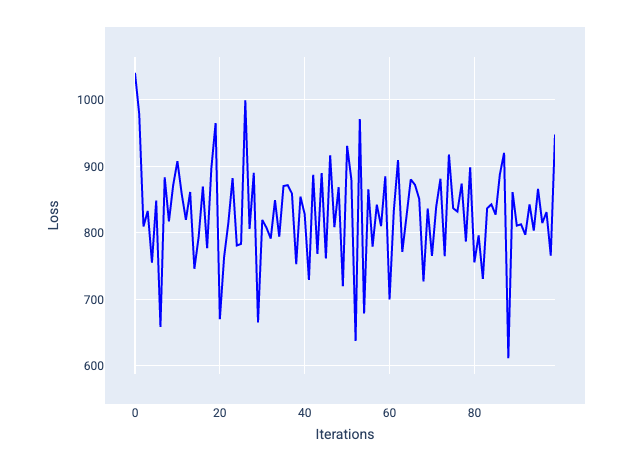
図 22. 学習率が大きすぎるモデルの損失グラフ。損失曲線が大きく変動し、イテレーションが増加するにつれて上下に変動しています。
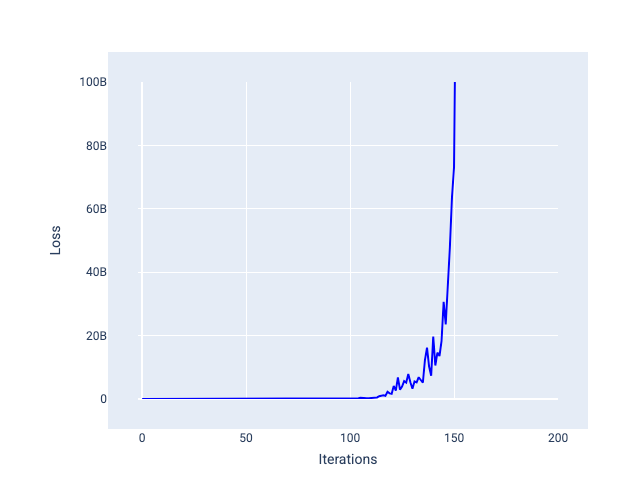
図 23. 学習率が大きすぎるモデルでトレーニングされた損失グラフ。損失曲線が後のイテレーションで急激に増加しています。
演習: 理解度を確認する
バッチサイズ
バッチサイズは、モデルが重みとバイアスを更新する前に処理する例の数を指すハイパーパラメータです。モデルは、重みとバイアスを更新する前に、データセット内のすべての例の損失を計算する必要があると思われるかもしれません。ただし、データセットに数十万、数百万もの例が含まれている場合は、フルバッチを使用するのは現実的ではありません。
重みとバイアスを更新する前にデータセット内のすべての例を確認しなくても、平均で適切な勾配を取得する一般的な手法は、確率的勾配降下法とミニバッチ確率的勾配降下法の 2 つです。
確率的勾配降下法(SGD): 確率的勾配降下法では、イテレーションごとに 1 つのサンプル(バッチサイズが 1)のみを使用します。十分な反復処理を行えば SGD は機能しますが、ノイズが非常に多くなります。「ノイズ」とは、トレーニング中に発生する変動のことで、イテレーション中に損失が減少するのではなく増加する原因となります。「確率的」という用語は、各バッチを構成する 1 つの例がランダムに選択されることを示します。
次の図では、モデルが SGD を使用して重みとバイアスを更新するにつれて損失がわずかに変動し、損失グラフにノイズが発生する様子が示されています。
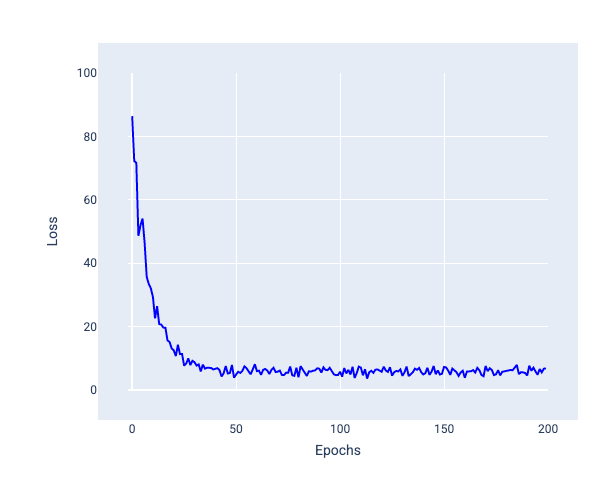
図 24. 確率的勾配降下法(SGD)でトレーニングされたモデルの損失曲線にノイズが見られる。
確率的勾配降下法を使用すると、収束付近だけでなく、損失曲線全体にノイズが発生する可能性があります。
ミニバッチ確率的勾配降下法(ミニバッチ SGD): ミニバッチ確率的勾配降下法は、フルバッチと SGD の折衷案です。$ N $ 個のデータポイントの場合、バッチサイズは 1 より大きく $ N $ より小さい任意の数にできます。モデルは、各バッチに含まれる例をランダムに選択し、勾配を平均化してから、反復ごとに重みとバイアスを 1 回更新します。
各バッチの例の数を決定するのは、データセットと利用可能なコンピューティング リソースによって異なります。一般に、バッチサイズが小さい場合は SGD のように動作し、バッチサイズが大きい場合はフルバッチ勾配降下法のように動作します。
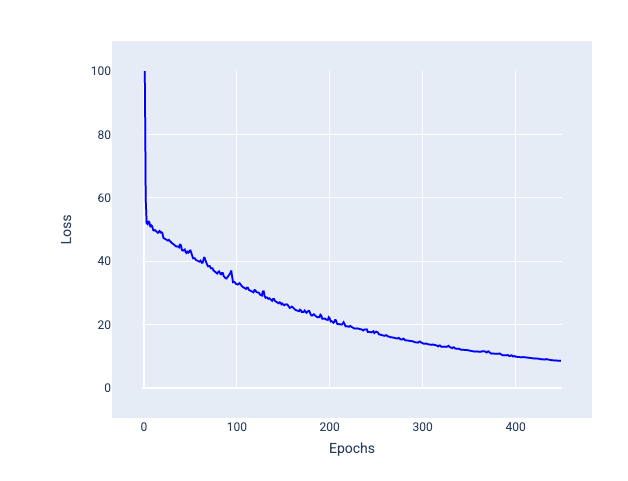
図 25. ミニバッチ SGD でトレーニングされたモデル。
モデルをトレーニングする際、ノイズは排除すべき望ましくない特性だと考えるかもしれません。ただし、ある程度のノイズは良い効果をもたらす可能性があります。以降のモジュールでは、ノイズがモデルの汎化を改善し、ニューラル ネットワークで最適な重みとバイアスを見つけるのに役立つ方法について学習します。
エポック
トレーニング中、エポックとは、モデルがトレーニング セット内のすべての例を 1 回処理したことを意味します。たとえば、1,000 個のサンプルを含むトレーニング セットと 100 個のサンプルのミニバッチサイズが指定されている場合、モデルが 1 エポックを完了するには 10 回のイテレーションが必要です。
通常、トレーニングには多くのエポックが必要です。つまり、システムはトレーニング セット内のすべての例を複数回処理する必要があります。
エポック数は、モデルのトレーニングを開始する前に設定するハイパーパラメータです。多くの場合、モデルが収束するまでに必要なエポック数を試す必要があります。一般に、エポック数が多いほどモデルの精度は向上しますが、トレーニングにかかる時間も長くなります。
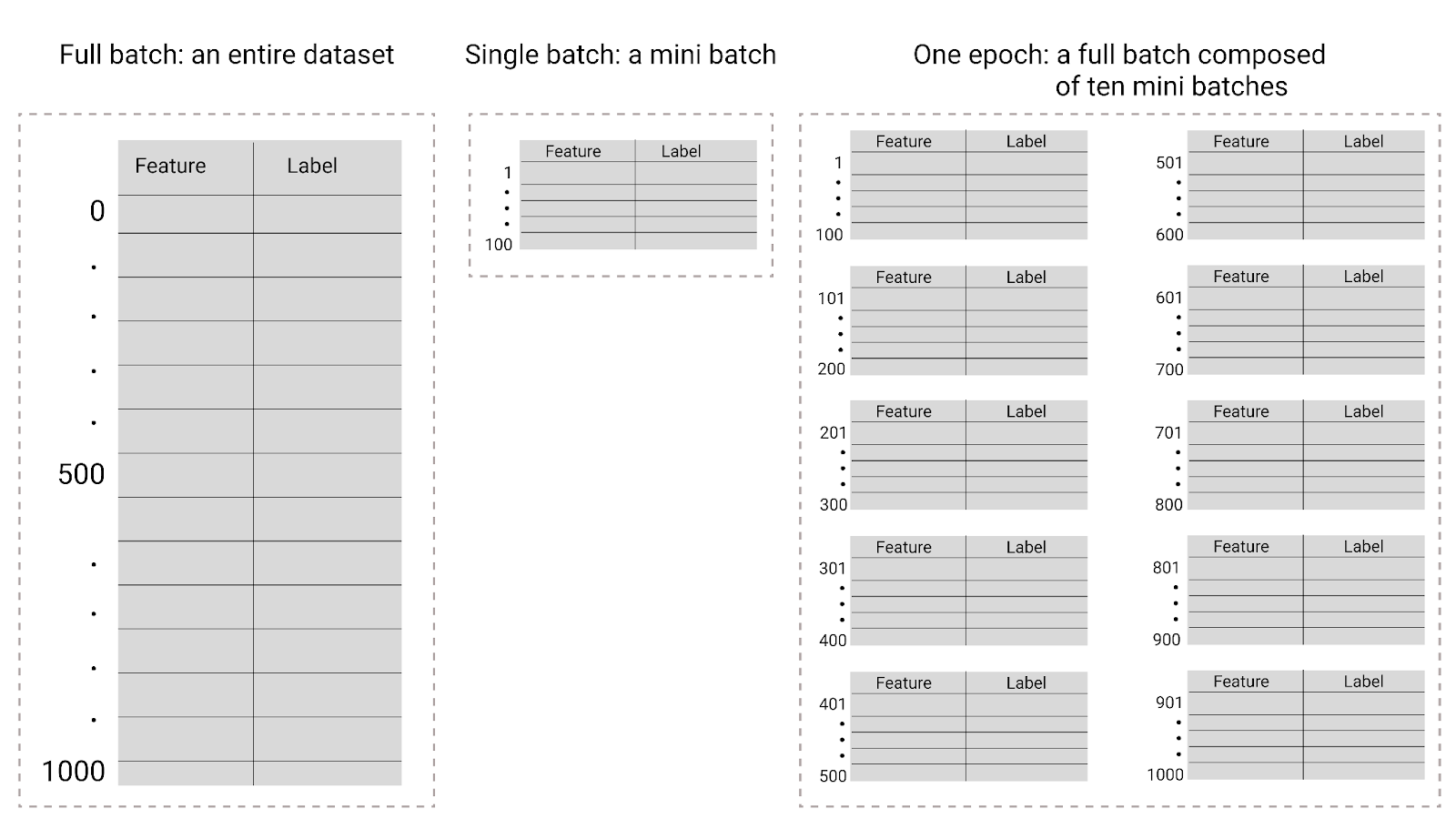
図 26. フルバッチとミニバッチ。
次の表に、バッチサイズとエポックがモデルのパラメータの更新回数にどのように関連するかを示します。
| バッチタイプ | 重みとバイアスの更新が発生するタイミング |
|---|---|
| フルバッチ | モデルがデータセット内のすべての例を確認した後。たとえば、データセットに 1,000 個のサンプルが含まれており、モデルが 20 エポックでトレーニングする場合、モデルはエポックごとに 1 回、重みとバイアスを 20 回更新します。 |
| 確率的勾配降下法 | モデルがデータセットの 1 つの例を調べた後。たとえば、データセットに 1,000 個のサンプルが含まれており、20 エポックでトレーニングする場合、モデルは重みとバイアスを 20,000 回更新します。 |
| ミニバッチ確率的勾配降下法 | モデルが各バッチの例を確認した後。たとえば、データセットに 1,000 個のサンプルが含まれており、バッチサイズが 100 で、モデルが 20 エポックでトレーニングされる場合、モデルは重みとバイアスを 200 回更新します。 |