La perdita è una metrica numerica che descrive quanto siano errate le previsioni di un modello. La perdita misura la distanza tra le previsioni del modello e le etichette effettive. L'obiettivo dell'addestramento di un modello è minimizzare la perdita, riducendola al suo valore più basso possibile.
Nell'immagine seguente puoi visualizzare la perdita come frecce disegnate dai punti dati al modello. Le frecce mostrano la distanza delle previsioni del modello dai valori effettivi.
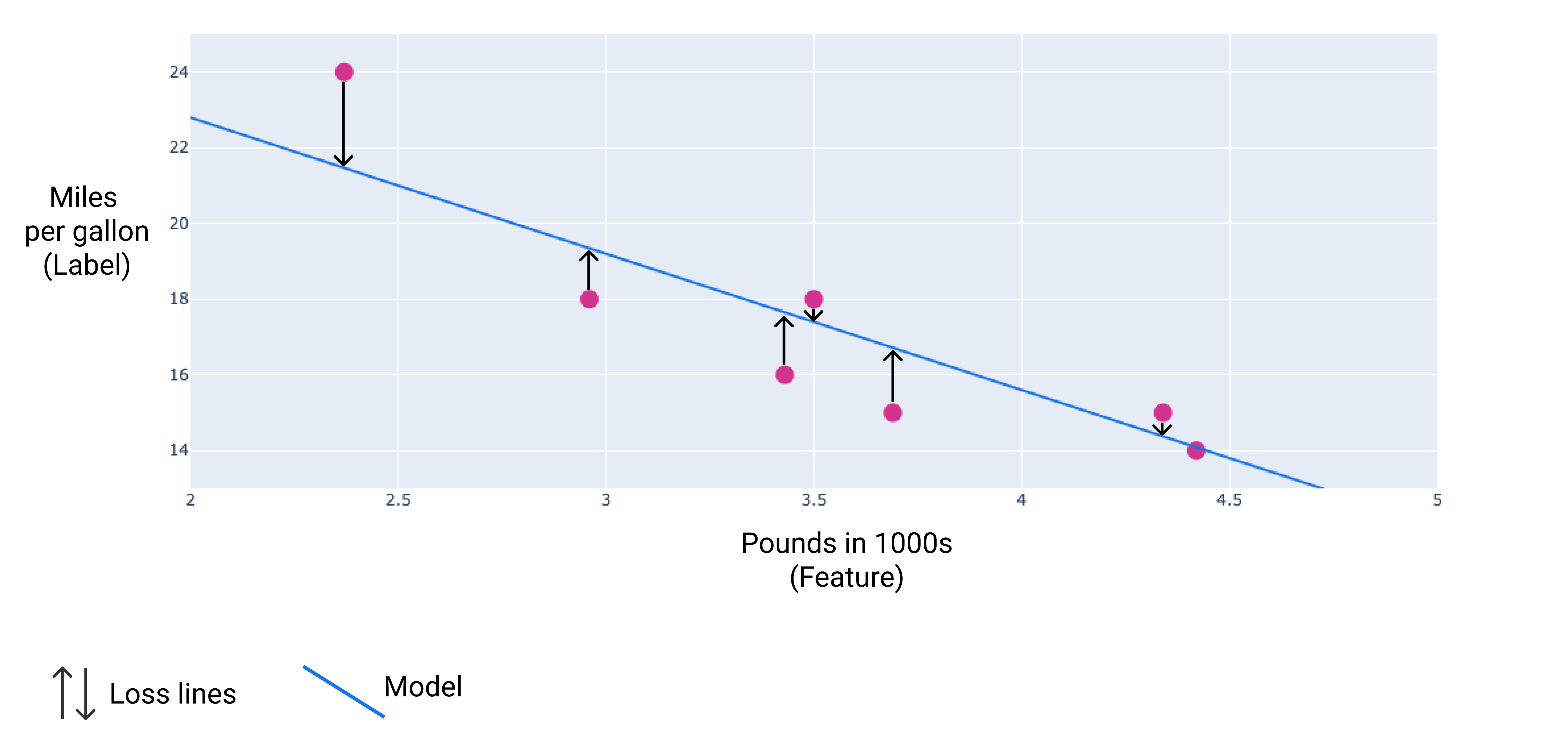
Figura 8. La perdita viene misurata dal valore effettivo al valore previsto.
Distanza di perdita
In statistica e machine learning, la perdita misura la differenza tra i valori previsti e quelli effettivi. La perdita si concentra sulla distanza tra i valori, non sulla direzione. Ad esempio, se un modello prevede 2, ma il valore effettivo è 5, non ci interessa che la perdita sia negativa ($ 2-5=-3 $). Ci interessa invece che la distanza tra i valori sia $ 3 $. Pertanto, tutti i metodi per calcolare la perdita rimuovono il segno.
I due metodi più comuni per rimuovere il segno sono i seguenti:
- Calcola il valore assoluto della differenza tra il valore effettivo e la previsione.
- Eleva al quadrato la differenza tra il valore effettivo e la previsione.
Tipi di perdita
Nella regressione lineare, esistono cinque tipi principali di perdita, descritti nella tabella seguente.
| Tipo di perdita | Definizione | Equazione |
|---|---|---|
| Perdita L1 | La somma dei valori assoluti della differenza tra i valori previsti e quelli effettivi. | $ ∑ | valore\ effettivo - valore\ previsto | $ |
| Errore assoluto medio (MAE) | La media delle perdite L1 in un insieme di N esempi. | $ \frac{1}{N} ∑ | valore\ effettivo - valore\ previsto | $ |
| L2 loss | La somma della differenza al quadrato tra i valori previsti e quelli effettivi. | $ ∑(valore\ effettivo - valore\ previsto)^2 $ |
| Errore quadratico medio (MSE) | La media delle perdite L2 in un insieme di N esempi. | $ \frac{1}{N} ∑ (valore\ effettivo - valore\ previsto)^2 $ |
| Errore quadratico medio (RMSE) | La radice quadrata dell'errore quadratico medio (MSE). | $ \sqrt{\frac{1}{N} ∑ (actual\ value - predicted\ value)^2} $ |
La differenza funzionale tra la perdita L1 e la perdita L2 (o tra MAE/RMSE e MSE) è l'elevazione al quadrato. Quando la differenza tra la previsione e l'etichetta è elevata, l'elevazione al quadrato aumenta ulteriormente la perdita. Quando la differenza è piccola (inferiore a 1), l'elevazione al quadrato rende la perdita ancora più piccola.
In alcuni casi d'uso, le metriche di perdita come MAE e RMSE potrebbero essere preferibili alla perdita L2 o all'errore quadratico medio (MSE) perché tendono a essere più interpretabili dall'uomo, in quanto misurano l'errore utilizzando la stessa scala del valore previsto del modello.
Quando elabori più esempi contemporaneamente, ti consigliamo di calcolare la media delle perdite in tutti gli esempi, indipendentemente dal fatto che utilizzi MAE, MSE o RMSE.
Esempio di calcolo della perdita
Utilizzando la migliore retta di regressione precedente, calcoleremo la perdita L2 per un singolo esempio. Dalla retta di miglior adattamento, abbiamo ottenuto i seguenti valori per ponderazione e bias:
- $ \small{Peso: -4,6} $
- $ \small{Bias: 34} $
Se il modello prevede che un'auto da 1075 kg consumi 10,2 km/l, ma in realtà consuma 11,1 km/l, calcoleremo la perdita L2 come segue:
| Valore | Equazione | Risultato |
|---|---|---|
| Previsione | $\small{bias + (weight * feature\ value)}$ $\small{34 + (-4.6*2.37)}$ |
$\small{23.1}$ |
| Valore effettivo | $ \small{ label } $ | $ \small{ 26 } $ |
| Perdita L2 | $ \small{ (valore\ effettivo - valore\ previsto)^2 } $ $\small{ (26 - 23.1)^2 }$ |
$\small{8.41}$ |
In questo esempio, la perdita L2 per quel singolo punto dati è 8,41.
Scegliere una perdita
La decisione di utilizzare MAE o MSE può dipendere dal set di dati e dal modo in cui vuoi gestire determinate previsioni. La maggior parte dei valori delle caratteristiche in un insieme di dati rientra in genere in un intervallo distinto. Ad esempio, le auto pesano normalmente tra 900 e 2200 kg e percorrono tra 3 e 21 km con un litro di carburante. Un'auto da 3600 kg o un'auto che percorre 160 km con un litro di carburante non rientra nell'intervallo tipico e sarebbe considerata un valore anomalo.
Un outlier può anche riferirsi alla distanza delle previsioni di un modello dai valori reali. Ad esempio, 3000 libbre rientrano nel tipico intervallo di peso delle auto e 40 miglia al gallone rientrano nel tipico intervallo di efficienza del carburante. Tuttavia, un'auto da 1360 kg che percorre 64 km con un gallone sarebbe un outlier in termini di previsione del modello, perché il modello prevede che un'auto da 1360 kg percorra circa 32 km con un gallone.
Quando scegli la funzione di perdita migliore, considera come vuoi che il modello tratti i valori anomali. Ad esempio, l'MSE sposta il modello più verso gli outlier, mentre il MAE non lo fa. La perdita L2 comporta una penalità molto più elevata per un outlier rispetto alla perdita L1. Ad esempio, le seguenti immagini mostrano un modello addestrato utilizzando MAE e un modello addestrato utilizzando MSE. La linea rossa rappresenta un modello completamente addestrato che verrà utilizzato per fare previsioni. Gli outlier sono più vicini al modello addestrato con MSE rispetto al modello addestrato con MAE.
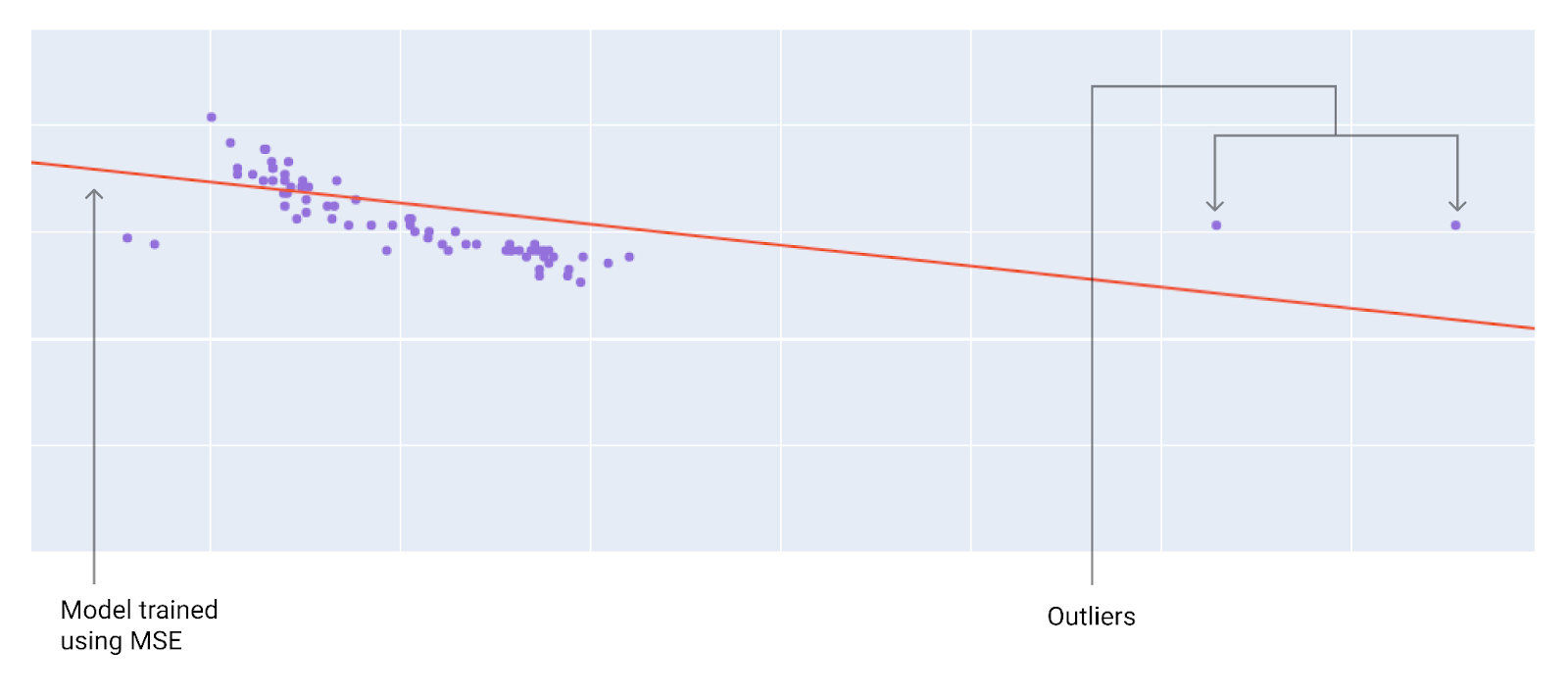
Figura 9. La perdita MSE avvicina il modello agli outlier.
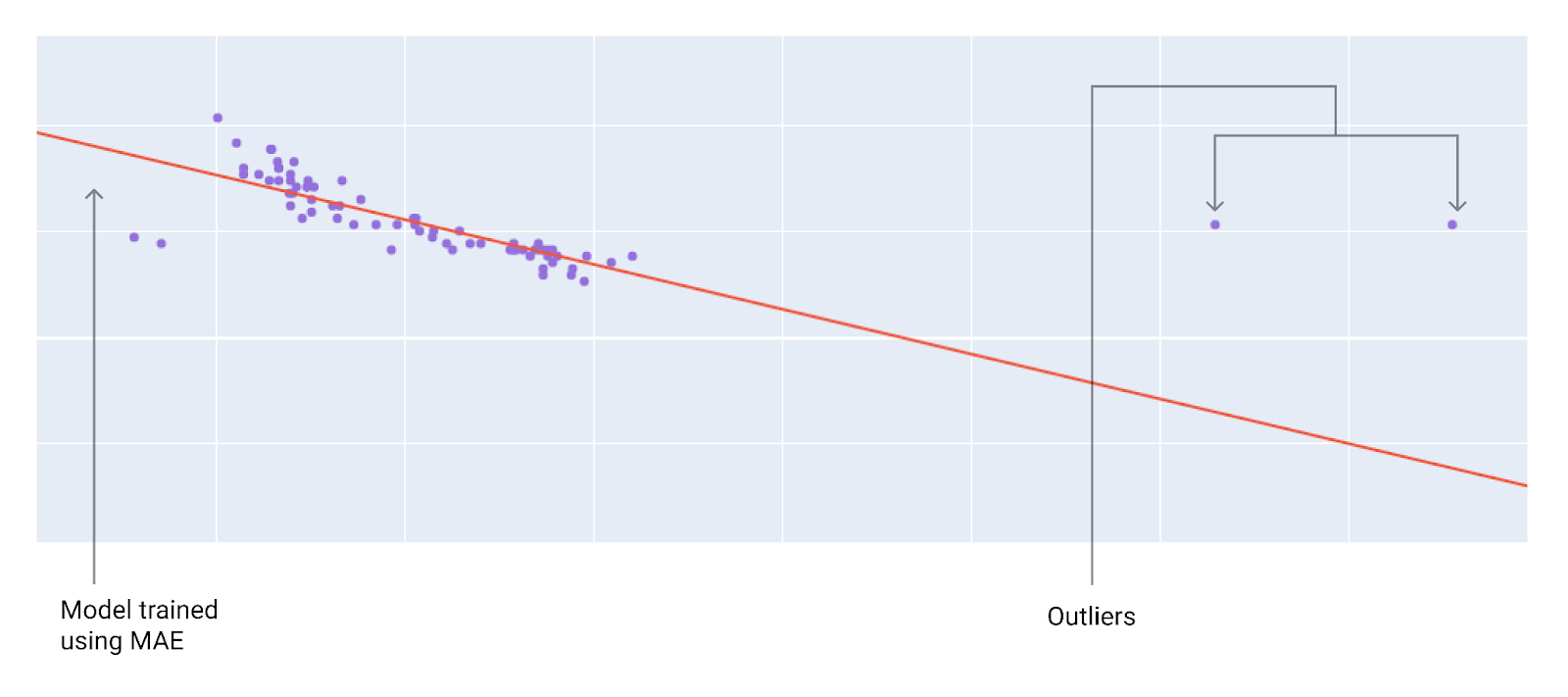
Figura 10. La perdita MAE mantiene il modello più lontano dagli outlier.
Tieni presente la relazione tra il modello e i dati:
MSE. Il modello è più vicino ai valori anomali, ma più lontano dalla maggior parte degli altri punti dati.
MAE. Il modello è più lontano dai valori anomali, ma più vicino alla maggior parte degli altri punti dati.
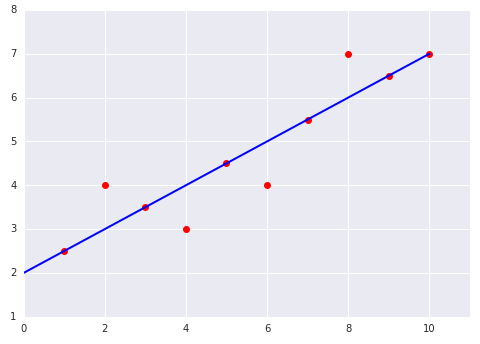
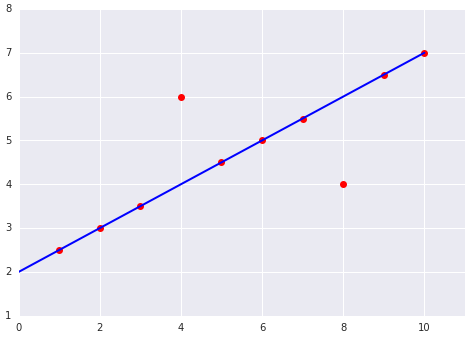
Verifica di aver compreso tutto
Considera i seguenti due grafici di un modello lineare adattato a un set di dati:
|
|
