Kayıp, modelin tahminlerinin ne kadar yanlış olduğunu açıklayan sayısal bir metriktir. Kayıp, modelin tahminleri ile gerçek etiketler arasındaki mesafeyi ölçer. Bir modeli eğitmenin amacı, kaybı en düşük olası değere indirerek en aza indirmektir.
Aşağıdaki resimde, veri noktalarından modele çizilen oklar olarak kaybı görselleştirebilirsiniz. Oklar, modelin tahminlerinin gerçek değerlerden ne kadar uzak olduğunu gösterir.
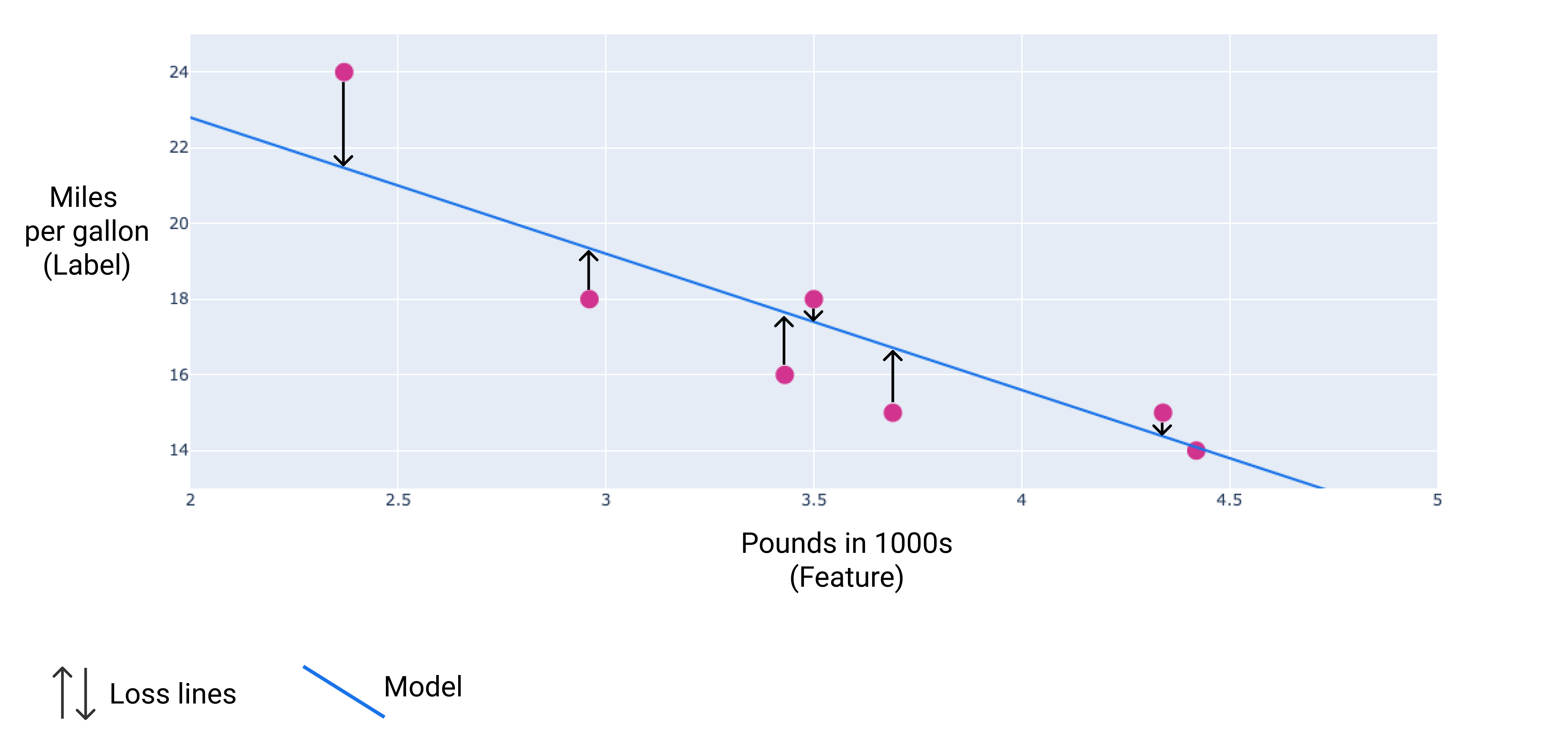
Şekil 8 Kayıp, gerçek değerden tahmin edilen değere kadar ölçülür.
Kayıp mesafesi
İstatistik ve makine öğreniminde kayıp, tahmin edilen değerler ile gerçek değerler arasındaki farkı ölçer. Kayıp, değerler arasındaki mesafeye odaklanır, yöne değil. Örneğin, bir model 2 tahmininde bulunuyorsa ancak gerçek değer 5 ise kaybın negatif olması (2 – 5= –3) bizim için önemli değildir. Bunun yerine, değerler arasındaki mesafenin 3 olmasını isteriz. Bu nedenle, kayıp hesaplamaya yönelik tüm yöntemlerde işaret kaldırılır.
İşareti kaldırmak için en yaygın kullanılan iki yöntem şunlardır:
- Gerçek değer ile tahmin arasındaki farkın mutlak değerini alın.
- Gerçek değer ile tahmin arasındaki farkın karesini alın.
Kayıp türleri
Doğrusal regresyonda beş ana kayıp türü vardır. Bunlar aşağıdaki tabloda özetlenmiştir.
| Kayıp türü | Tanım | Denklem |
|---|---|---|
| L1 kaybı | Tahmin edilen değerler ile gerçek değerler arasındaki farkın mutlak değerlerinin toplamı. | $ ∑ | gerçek\ değer - tahmini\ değer | $ |
| Ortalama mutlak hata (MAE) | Bir dizi N örnekteki L1 kayıplarının ortalaması. | $ \frac{1}{N} ∑ | actual\ value - predicted\ value | $ |
| L2 kaybı | Tahmin edilen değerler ile gerçek değerler arasındaki kare farkının toplamı. | $ ∑(gerçek\ değer - tahmin\ edilen\ değer)^2 $ |
| Ortalama karesel hata (MSE) | N örnekten oluşan bir gruptaki L2 kayıplarının ortalaması. | $ \frac{1}{N} ∑ (actual\ value - predicted\ value)^2 $ |
| Kök ortalama kare hatası (RMSE) | Ortalama karesel hatanın (MSE) karekökü. | $ \sqrt{\frac{1}{N} ∑ (actual\ value - predicted\ value)^2} $ |
L1 kaybı ile L2 kaybı (veya MAE/RMSE ile MSE) arasındaki işlevsel fark, karesini almaktır. Tahmin ile etiket arasındaki fark büyük olduğunda kare alma işlemi kaybı daha da artırır. Fark küçük olduğunda (1'den az) kare alma işlemi kaybı daha da küçültür.
MAE ve RMSE gibi kayıp metrikleri, L2 kaybı veya MSE'ye göre bazı kullanım alanlarında tercih edilebilir. Bunun nedeni, hatayı modelin tahmin edilen değeriyle aynı ölçekte ölçtükleri için daha kolay yorumlanabilmeleridir.
MAE, MSE veya RMSE kullanırken aynı anda birden fazla örnek işleniyorsa tüm örneklerdeki kayıpların ortalamasını almanızı öneririz.
Kayıp hesaplama örneği
Önceki bölümde, yakıt verimliliğini arabanın ağırlığına göre tahmin etmek için aşağıdaki modeli oluşturduk:
- Model: $ y' = 34 + (-4.6)(x_1) $
- Ağırlık: $ –4.6 $
- Yanlılık: 34 ABD doları
Model,1.075 kg ağırlığındaki bir arabanın 1 litre yakıtla 9, 8 km yol gideceğini tahmin ediyorsa ancak gerçekte 1 litre yakıtla 10, 2 km yol gidiyorsa L2 kaybını aşağıdaki şekilde hesaplarız:
| Değer | Denklem | Sonuç |
|---|---|---|
| Tahmin | $\small{bias + (weight * feature\ value)}$ $\small{34 + (-4.6*2.37)}$ |
$\small{23.1}$ |
| Gerçek değer | $ \small{ label } $ | $ \small{ 24 } $ |
| L2 kaybı | $ \small{ (actual\ value - predicted\ value)^2 } $ $\small{ (24 - 23.1)^2 }$ |
$\small{0.81}$ |
Bu örnekte, tek bir veri noktası için L2 kaybı 0,81'dir.
Kayıp seçme
MAE veya MSE kullanıp kullanmayacağınıza karar verirken veri kümesini ve belirli tahminleri nasıl ele almak istediğinizi göz önünde bulundurabilirsiniz. Bir veri kümesindeki çoğu özellik değeri genellikle belirli bir aralıkta yer alır. Örneğin, arabalar normalde 900 kg ile 2.250 kg arasında ağırlığa sahiptir ve galon başına 3 ile 21 km arasında yol kat eder. 3.600 kg ağırlığındaki veya 100 mil/galon yakıt tüketen bir araba, normal aralığın dışındadır ve aykırı değer olarak kabul edilir.
Aykırı değer, bir modelin tahminlerinin gerçek değerlerden ne kadar uzak olduğunu da ifade edebilir. Örneğin, 3.000 pound tipik araç ağırlığı aralığındadır ve galon başına 40 mil tipik yakıt verimliliği aralığındadır. Ancak, galon başına 40 mil yol kat eden 3.000 pound ağırlığındaki bir araba,modelin tahmini açısından aykırı değer olur. Çünkü model,3.000 pound ağırlığındaki bir arabanın galon başına yaklaşık 20 mil yol kat edeceğini tahmin eder.
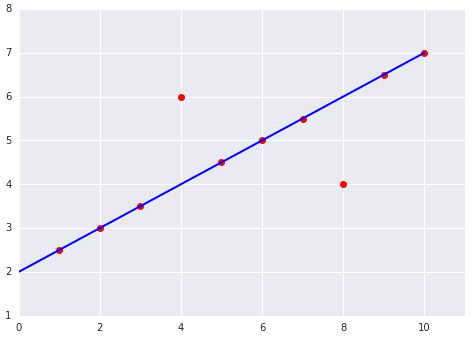
En iyi kayıp işlevini seçerken modelin aykırı değerleri nasıl ele almasını istediğinizi göz önünde bulundurun. Örneğin, MSE modeli aykırı değerlere doğru kaydırırken MAE bunu yapmaz. L2 kaybı, aykırı değer için L1 kaybından çok daha yüksek bir ceza alır. Örneğin, aşağıdaki resimlerde MAE kullanılarak eğitilmiş bir model ve MSE kullanılarak eğitilmiş bir model gösterilmektedir. Kırmızı çizgi, tahmin yapmak için kullanılacak tam olarak eğitilmiş bir modeli temsil eder. Aykırı değerler, MAE ile eğitilen modelden ziyade MSE ile eğitilen modele daha yakındır.
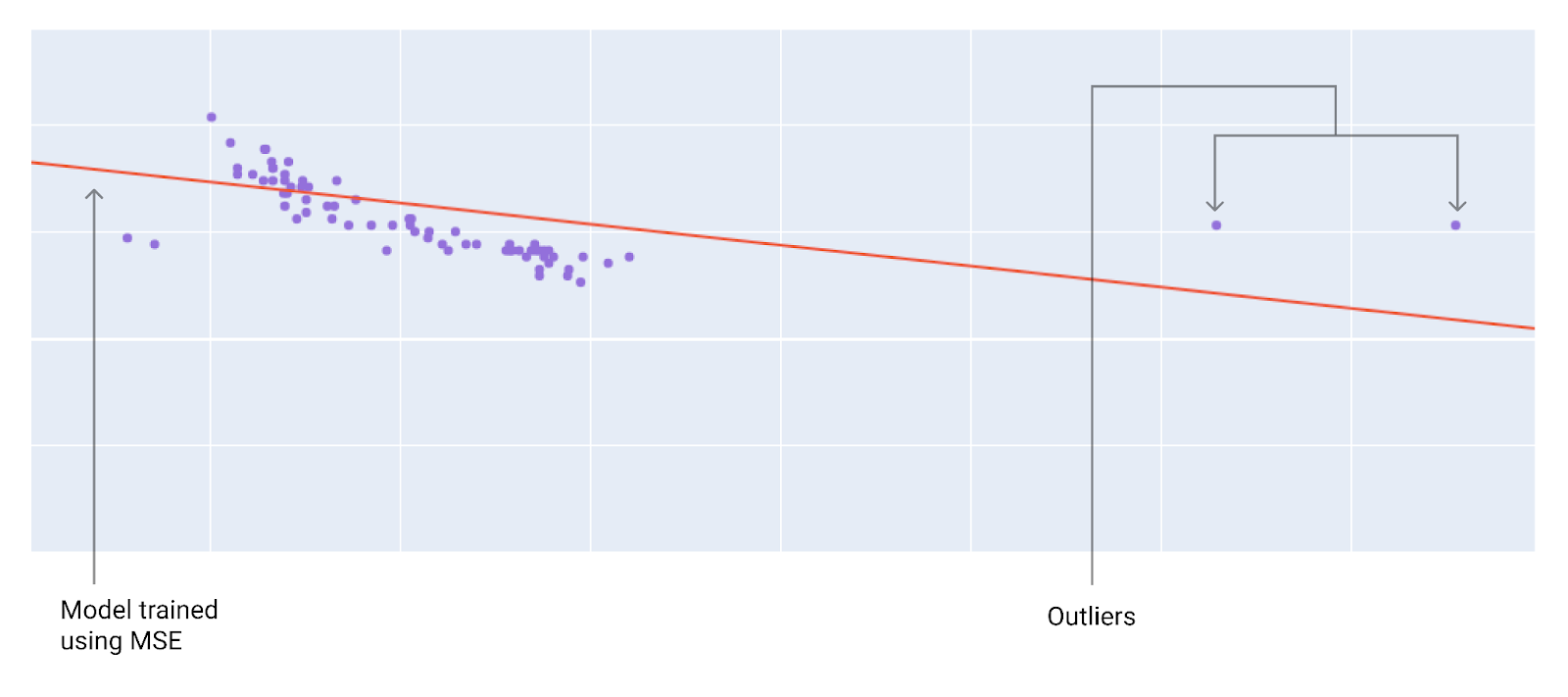
Şekil 9. MSE kaybı, modeli aykırı değerlere yaklaştırır.
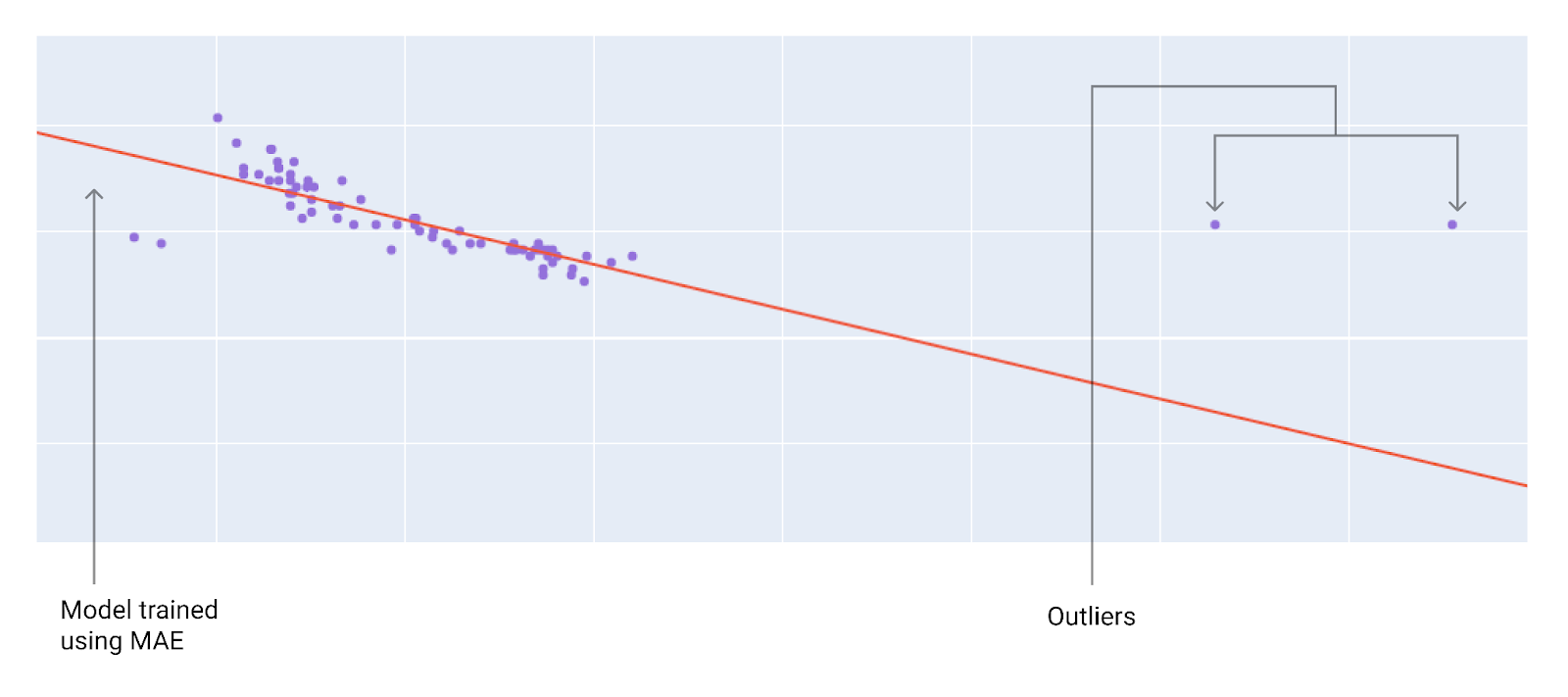
Şekil 10. MAE kaybı, modeli aykırı değerlerden daha uzak tutar.
Model ile veriler arasındaki ilişkiye dikkat edin:
MSE. Model, aykırı değerlere daha yakın ancak diğer veri noktalarının çoğundan daha uzaktır.
MAE. Model, aykırı değerlerden daha uzakta ancak diğer veri noktalarının çoğuna daha yakındır.
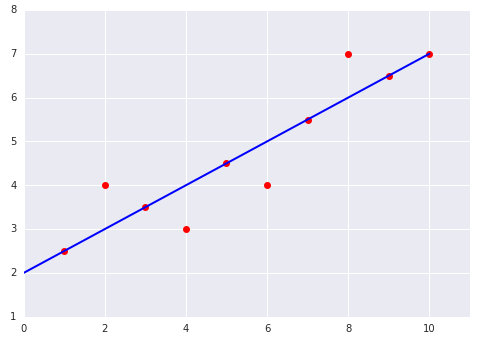
Anlayıp anlamadığınızı kontrol etme
Bir veri kümesine uyan doğrusal modelin aşağıdaki iki grafiğini inceleyin:
|
|
