Функция потерь — это числовая метрика, описывающая, насколько неверны предсказания модели. Функция потерь измеряет расстояние между предсказаниями модели и фактическими метками. Цель обучения модели — минимизировать функцию потерь, сводя её к минимально возможному значению.
На следующем изображении вы можете визуализировать потери в виде стрелок, проведенных от точек данных к модели. Стрелки показывают, насколько предсказания модели отличаются от фактических значений.
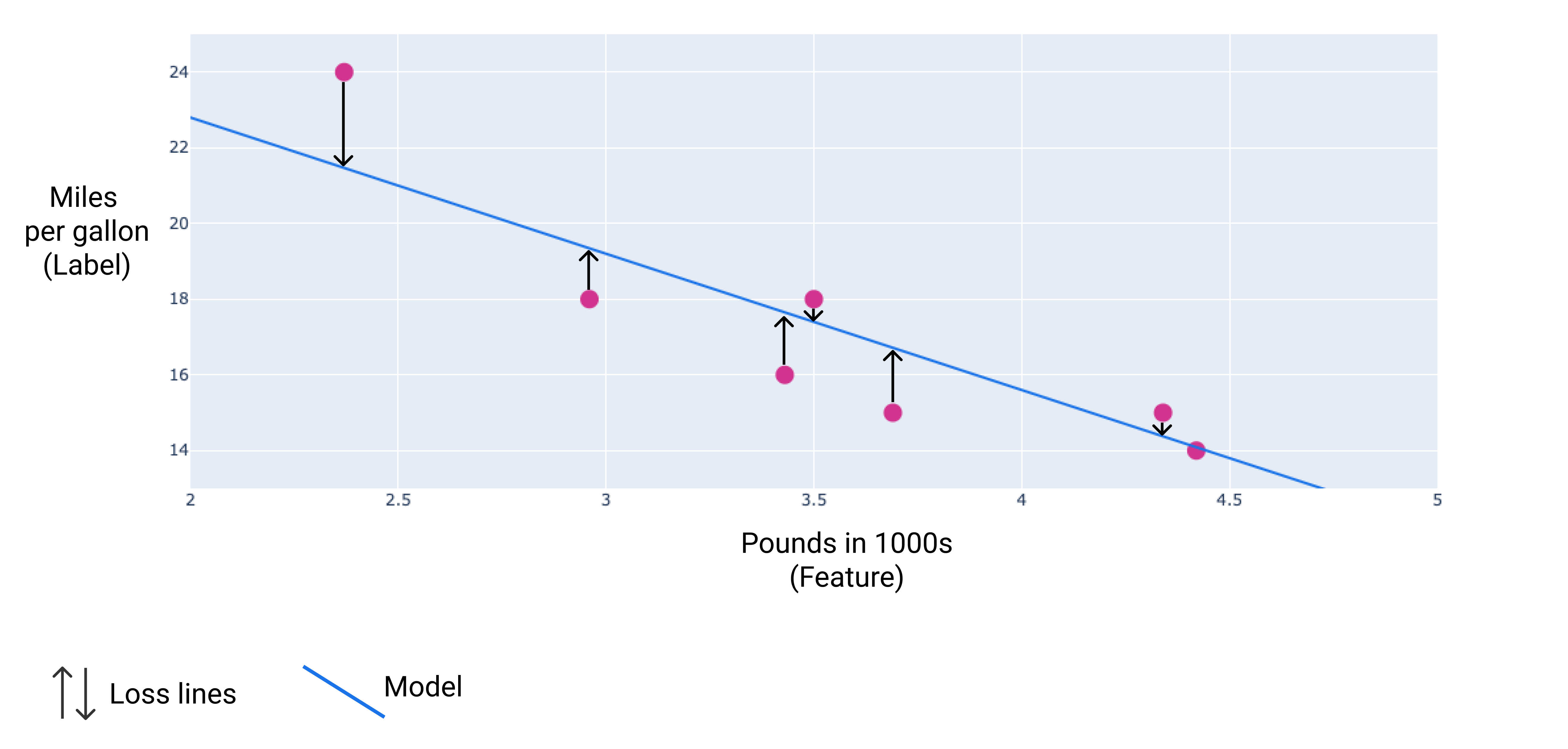
Figure 8 . Loss is measured from the actual value to the predicted value.
Расстояние потери
In statistics and machine learning, loss measures the difference between the predicted and actual values. Loss focuses on the distance between the values, not the direction. For example, if a model predicts 2, but the actual value is 5, we don't care that the loss is negative (2 – 5= –3). Instead, we care that the distance between the values is 3. Thus, all methods for calculating loss remove the sign.
Наиболее распространенные способы снятия вывески следующие:
- Возьмите абсолютное значение разницы между фактическим значением и прогнозом.
- Возведите в квадрат разницу между фактическим значением и прогнозом.
Виды убытков
В линейной регрессии существует пять основных типов потерь, которые описаны в следующей таблице.
| тип убытка | Определение | Уравнение |
|---|---|---|
| L 1 loss | Сумма абсолютных значений разницы между прогнозируемыми и фактическими значениями. | $ ∑ | фактическое значение - прогнозируемое значение | $ |
| Средняя абсолютная ошибка (MAE) | The average of L 1 losses across a set of N examples. | $ \frac{1}{N} ∑ | фактическое значение - прогнозируемое значение | $ |
| L 2 loss | Сумма квадратов разностей между прогнозируемыми и фактическими значениями. | $ ∑(фактическое значение - прогнозируемое значение)^2 $ |
| Среднеквадратичная ошибка (MSE) | The average of L 2 losses across a set of N examples. | $ \frac{1}{N} ∑ (фактическое значение - прогнозируемое значение)^2 $ |
| Среднеквадратичная ошибка (RMSE) | Квадратный корень из среднеквадратичной ошибки (MSE). | $ \sqrt{\frac{1}{N} ∑ (фактическое значение - прогнозируемое значение)^2} $ |
Функциональное различие между функцией потерь L1 и функцией потерь L2 (или между MAE/RMSE и MSE) заключается в возведении в квадрат. Когда разница между предсказанием и меткой велика, возведение в квадрат еще больше увеличивает функцию потерь. Когда разница мала (меньше 1), возведение в квадрат еще меньше уменьшает функцию потерь.
Loss metrics like MAE and RMSE may be preferable to L 2 loss or MSE in some use cases because they tend to be more human-interpretable, as they measure error using the same scale as the model's predicted value.
При обработке нескольких примеров одновременно рекомендуется усреднять значения потерь по всем примерам, используя MAE, MSE или RMSE.
Пример расчета убытков
В предыдущем разделе мы создали следующую модель для прогнозирования топливной эффективности в зависимости от веса автомобиля:
- Модель: $ y' = 34 + (-4,6)(x_1) $
- Вес: –4,6 $
- Предвзятость: 34 доллара
If the model predicts that a 2,370-pound car gets 23.1 miles per gallon, but it actually gets 24 miles per gallon, we would calculate the L 2 loss as follows:
| Ценить | Уравнение | Результат |
|---|---|---|
| Прогноз | $\small{bias + (weight * feature\ value)}$ $\small{34 + (-4.6*2.37)}$ | $\small{23.1}$ |
| Фактическая стоимость | $ \small{ label } $ | $ \small{ 24 } $ |
| L 2 loss | $ \small{ (фактическое значение - прогнозируемое значение)^2 } $ $\small{ (24 - 23.1)^2 }$ | $\small{0.81}$ |
In this example, the L 2 loss for that single data point is 0.81.
Выбор проигрыша
Deciding whether to use MAE or MSE can depend on the dataset and the way you want to handle certain predictions. Most feature values in a dataset typically fall within a distinct range. For example, cars are normally between 2000 and 5000 pounds and get between 8 to 50 miles per gallon. An 8,000-pound car, or a car that gets 100 miles per gallon, is outside the typical range and would be considered an outlier .
Выброс также может означать, насколько сильно прогнозы модели отличаются от реальных значений. Например, 3000 фунтов находятся в пределах типичного диапазона веса автомобиля, а 40 миль на галлон — в пределах типичного диапазона топливной экономичности. Однако автомобиль весом 3000 фунтов, расходующий 40 миль на галлон, будет выбросом с точки зрения прогноза модели, поскольку модель предскажет, что автомобиль весом 3000 фунтов будет расходовать около 20 миль на галлон.
When choosing the best loss function, consider how you want the model to treat outliers. For instance, MSE moves the model more toward the outliers, while MAE doesn't. L 2 loss incurs a much higher penalty for an outlier than L 1 loss. For example, the following images show a model trained using MAE and a model trained using MSE. The red line represents a fully trained model that will be used to make predictions. The outliers are closer to the model trained with MSE than to the model trained with MAE.
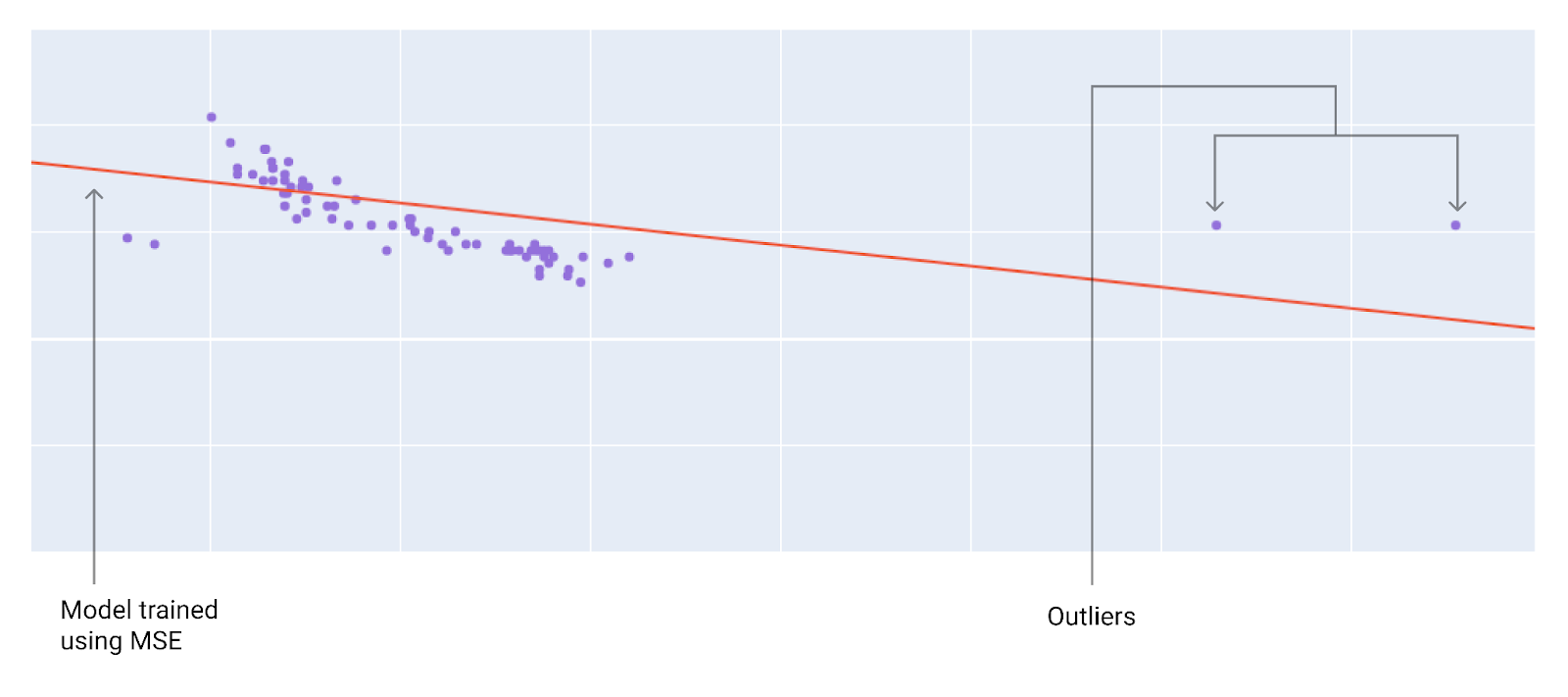
Figure 9 . MSE loss moves the model closer to the outliers.
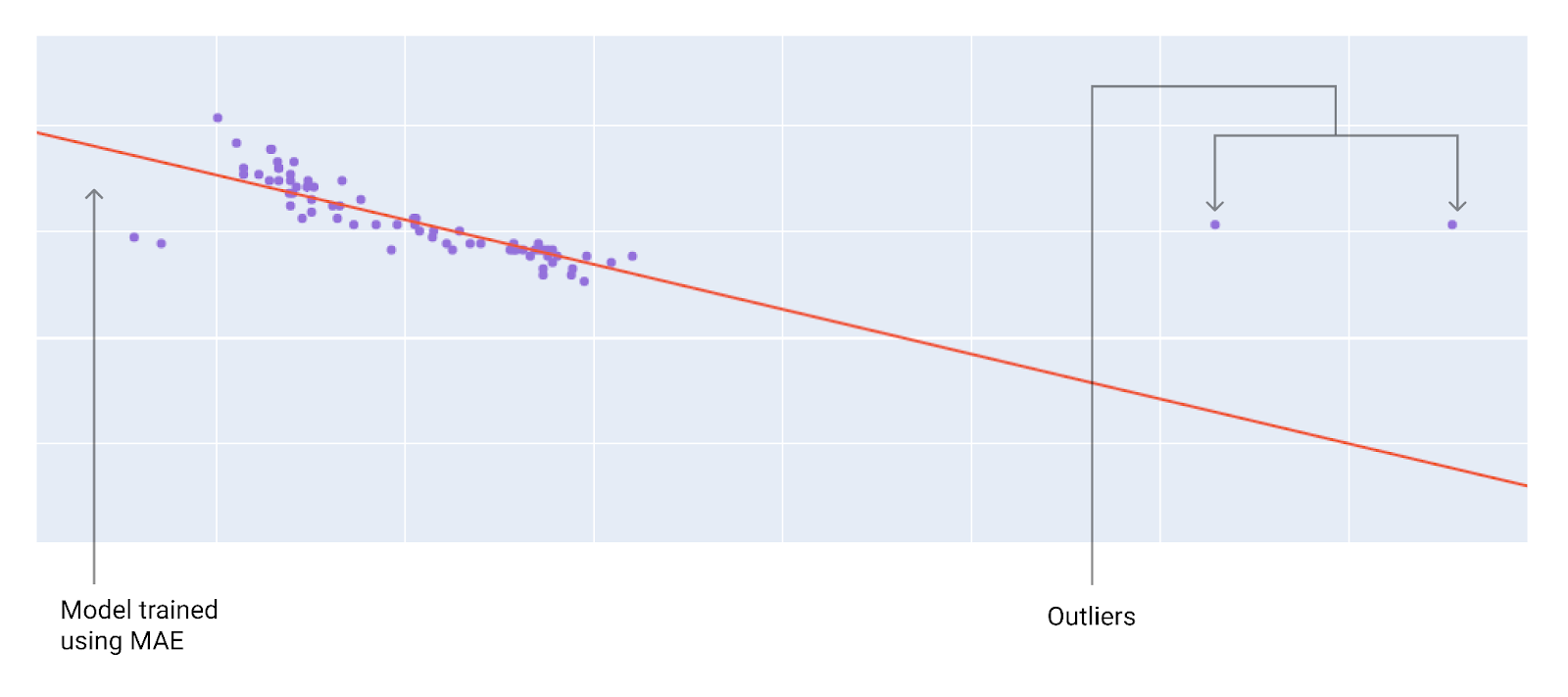
Figure 10 . MAE loss keeps the model farther from the outliers.
Обратите внимание на взаимосвязь между моделью и данными:
Среднеквадратичная ошибка (MSE) . Модель ближе к выбросам, но дальше от большинства других точек данных.
MAE . The model is further away from the outliers but closer to most of the other data points.
Проверьте свои знания
Рассмотрим следующие два графика линейной модели, построенной на основе набора данных:
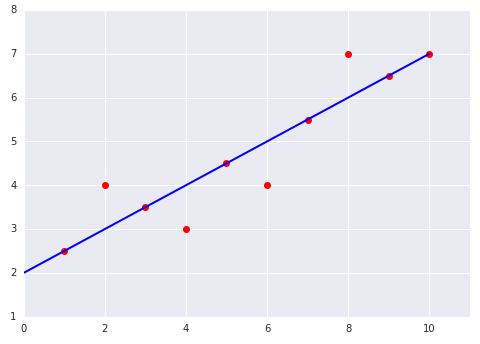 | 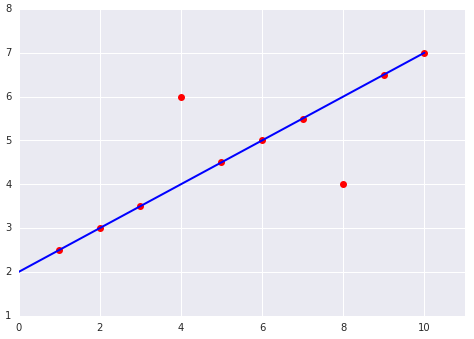 |
