La perte est une métrique numérique qui décrit le degré d'inexactitude des prédictions d'un modèle. La perte mesure la distance entre les prédictions du modèle et les libellés réels. L'objectif de l'entraînement d'un modèle est de minimiser la perte, en la réduisant à sa valeur la plus basse possible.
Dans l'image suivante, vous pouvez visualiser la perte sous forme de flèches tracées à partir des points de données vers le modèle. Les flèches indiquent l'écart entre les prédictions du modèle et les valeurs réelles.
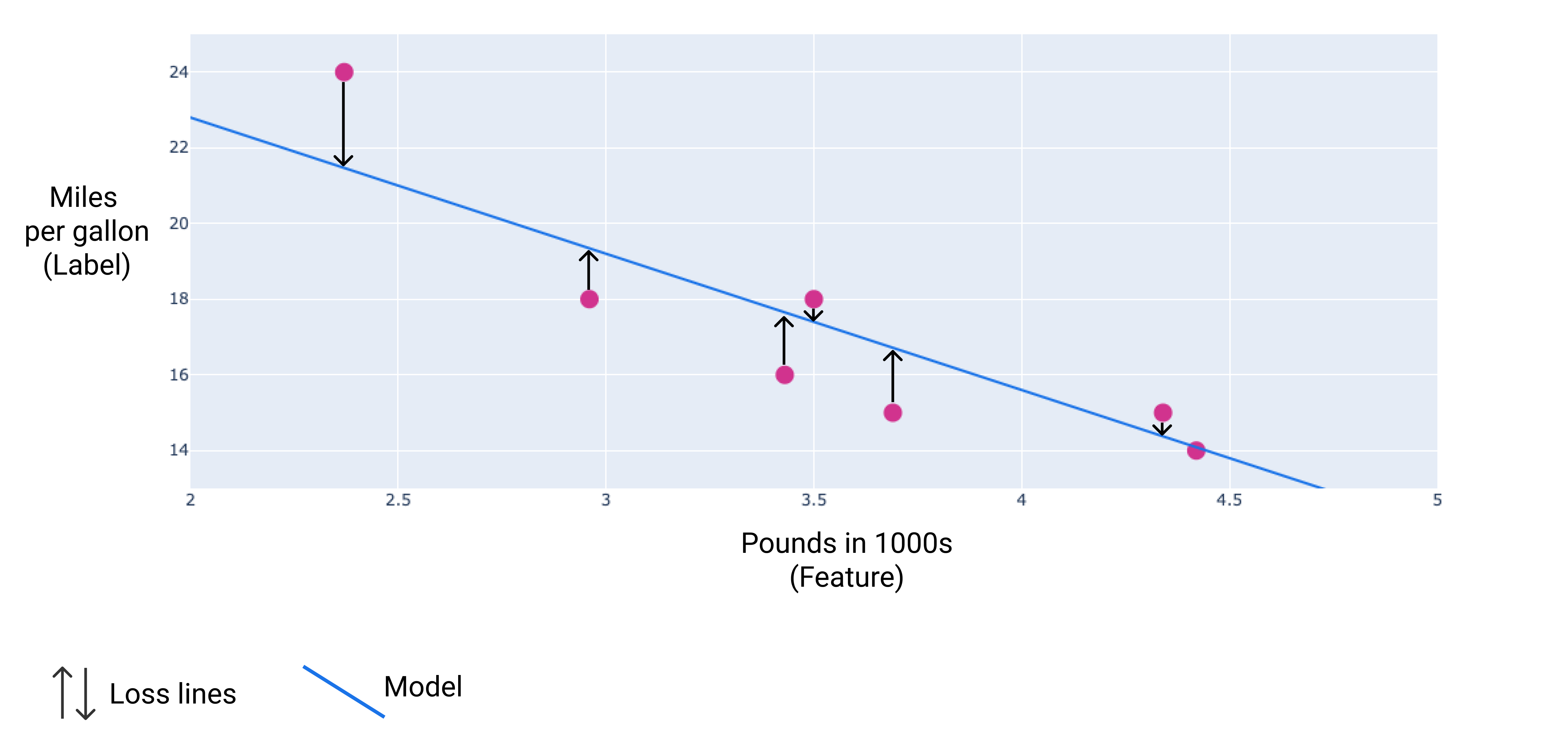
Figure 8. La perte est mesurée à partir de la valeur réelle jusqu'à la valeur prédite.
Distance de perte
En statistiques et en machine learning, la perte mesure la différence entre les valeurs prédites et réelles. La perte se concentre sur la distance entre les valeurs, et non sur la direction. Par exemple, si un modèle prédit la valeur 2, mais que la valeur réelle est 5, la perte négative (2 – 5= –3) n'a pas d'importance. Ce qui nous intéresse, c'est que la distance entre les valeurs soit de 3. Par conséquent, toutes les méthodes de calcul de la perte suppriment le signe.
Voici les deux méthodes les plus courantes pour supprimer le signe :
- Prenez la valeur absolue de la différence entre la valeur réelle et la prédiction.
- Mettez au carré la différence entre la valeur réelle et la prédiction.
Types de pertes
Dans la régression linéaire, il existe cinq principaux types de pertes, qui sont décrits dans le tableau suivant.
| Type de perte | Définition | Équation |
|---|---|---|
| Perte L1 | Somme des valeurs absolues de la différence entre les valeurs prédites et les valeurs réelles. | $ ∑ | valeur\ réelle - valeur\ prédite | $ |
| Erreur absolue moyenne (EAM) | Moyenne des pertes L1 pour un ensemble de N exemples. | $ \frac{1}{N} ∑ | valeur\ réelle - valeur\ prédite | $ |
| Perte L | La somme des différences au carré entre les valeurs prédites et les valeurs réelles. | $ ∑(valeur\ réelle - valeur\ prédite)^2 $ |
| Erreur quadratique moyenne (MSE) | Moyenne des pertes L2 pour un ensemble de N exemples. | $ \frac{1}{N} ∑ (valeur\ réelle - valeur\ prédite)^2 $ |
| Racine carrée de l'erreur quadratique moyenne (RMSE) | Racine carrée de l'erreur quadratique moyenne (MSE). | $ \sqrt{\frac{1}{N} ∑ (valeur\ réelle - valeur\ prédite)^2} $ |
La différence fonctionnelle entre la perte L1 et la perte L2 (ou entre MAE/RMSE et MSE) est la mise au carré. Lorsque la différence entre la prédiction et le libellé est importante, la mise au carré augmente encore la perte. Lorsque la différence est faible (inférieure à 1), la mise au carré réduit encore la perte.
Les métriques de perte telles que l'EAM et la RMSE peuvent être préférables à la perte L2 ou à l'erreur quadratique moyenne dans certains cas d'utilisation, car elles ont tendance à être plus faciles à interpréter par les humains. En effet, elles mesurent l'erreur à l'aide de la même échelle que la valeur prédite du modèle.
Lorsque vous traitez plusieurs exemples à la fois, nous vous recommandons de calculer la moyenne des pertes pour tous les exemples, que vous utilisiez MAE, MSE ou RMSE.
Exemple de calcul de la perte
Dans la section précédente, nous avons créé le modèle suivant pour prédire l'efficacité énergétique en fonction du poids de la voiture :
- Modèle : $ y' = 34 + (-4.6)(x_1) $
- Poids : $ –4.6 $
- Biais : $ 34 $
Si le modèle prédit qu'une voiture de 1 075 kg consomme 10,2 l/100 km, mais qu'elle consomme en réalité 9,8 l/100 km, nous calculerons la perte L2 comme suit :
| Valeur | Équation | Résultat |
|---|---|---|
| Prédiction | $\small{biais + (poids * valeur\ de\ la\ caractéristique)}$ $\small{34 + (-4.6*2.37)}$ |
$\small{23.1}$ |
| Valeur réelle | $ \small{ label } $ | $ \small{ 24 } $ |
| Perte L2 | $ \small{ (valeur\ réelle - valeur\ prédite)^2 } $ $\small{ (24 - 23.1)^2 }$ |
$\small{0.81}$ |
Dans cet exemple, la perte L2 pour ce point de données unique est de 0,81.
Choisir une perte
Le choix entre la MAE et la MSE peut dépendre de l'ensemble de données et de la façon dont vous souhaitez gérer certaines prédictions. La plupart des valeurs de caractéristiques d'un ensemble de données se situent généralement dans une plage distincte. Par exemple, les voitures pèsent normalement entre 900 et 2 200 kg et consomment entre 4 et 20 litres aux 100 km. Une voiture de 3 600 kg ou une voiture qui consomme 2,35 l/100 km se situe en dehors de la plage habituelle et serait considérée comme une valeur aberrante.
Un outlier peut également faire référence à l'écart entre les prédictions d'un modèle et les valeurs réelles. Par exemple, 1 360 kg se situe dans la plage de poids typique d'une voiture, et 17 km/l se situe dans la plage d'efficacité énergétique typique. Toutefois, une voiture de 1 360 kg qui consomme 5,9 l/100 km serait une valeur aberrante en termes de prédiction du modèle, car le modèle prédirait qu'une voiture de 1 360 kg consommerait environ 11,8 l/100 km.
Lorsque vous choisissez la meilleure fonction de perte, réfléchissez à la façon dont vous souhaitez que le modèle traite les valeurs aberrantes. Par exemple, la MSE rapproche davantage le modèle des valeurs aberrantes, contrairement à la MAE. La perte L2 entraîne une pénalité beaucoup plus élevée pour une valeur aberrante que la perte L1. Par exemple, les images suivantes montrent un modèle entraîné à l'aide de la MAE et un modèle entraîné à l'aide de la MSE. La ligne rouge représente un modèle entièrement entraîné qui sera utilisé pour effectuer des prédictions. Les valeurs aberrantes sont plus proches du modèle entraîné avec MSE que du modèle entraîné avec MAE.
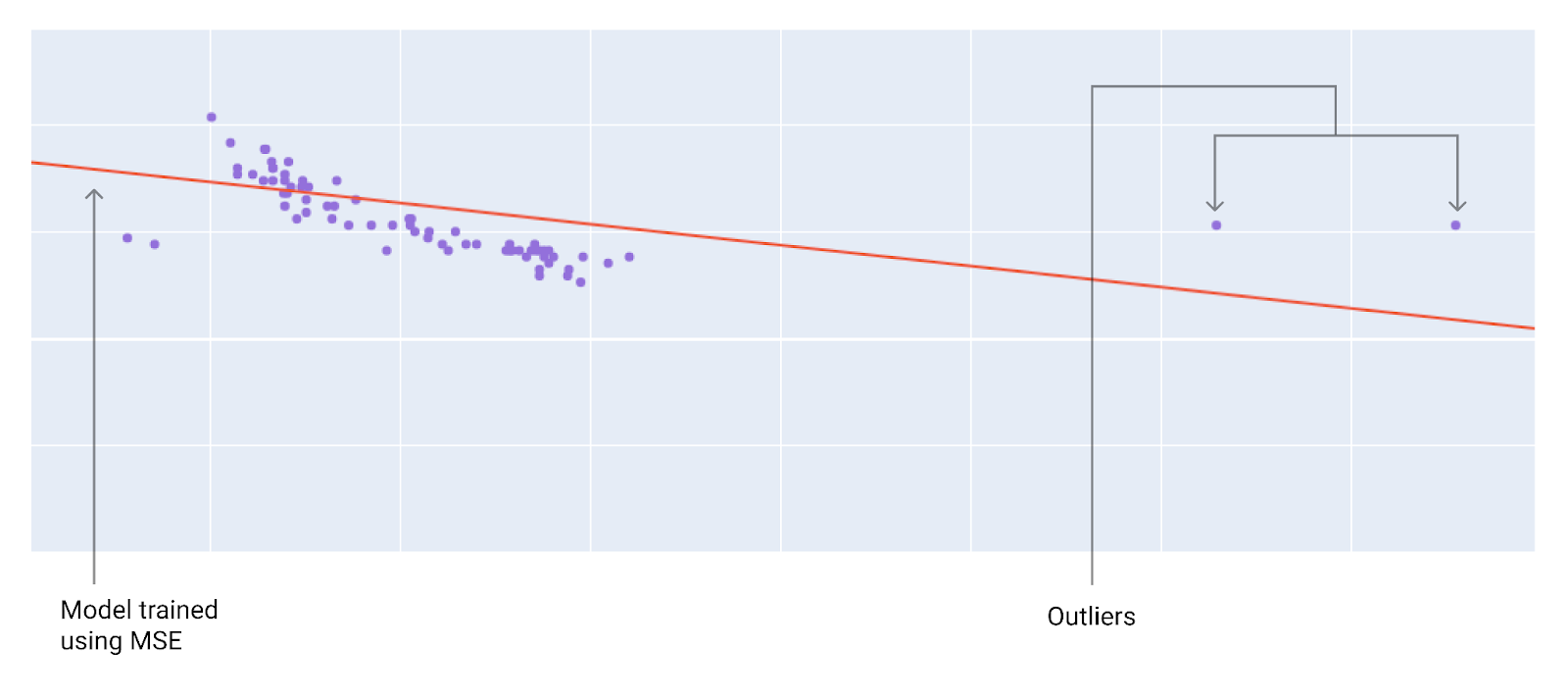
Figure 9. La perte MSE rapproche le modèle des valeurs aberrantes.
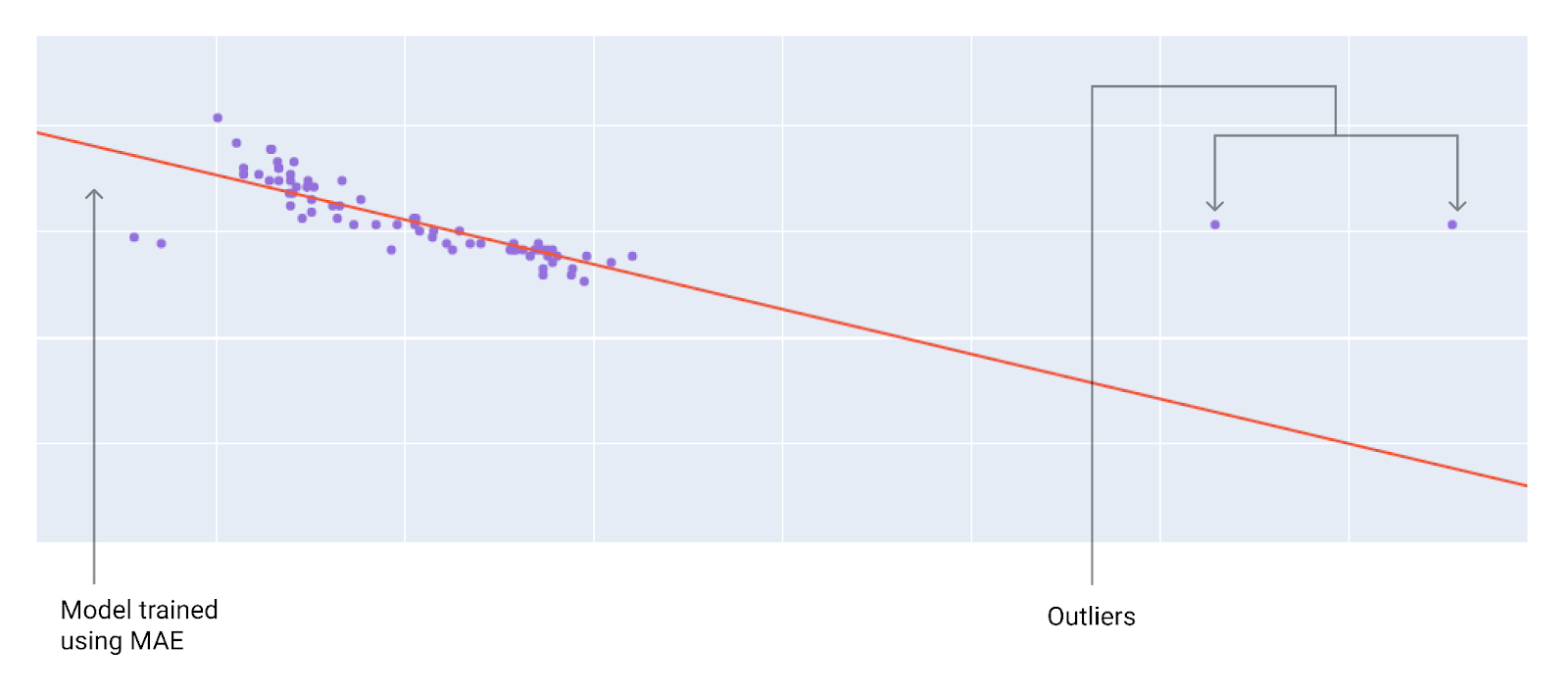
Figure 10 : La perte MAE maintient le modèle plus éloigné des valeurs aberrantes.
Notez la relation entre le modèle et les données :
MSE. Le modèle est plus proche des valeurs aberrantes, mais plus éloigné de la plupart des autres points de données.
MAE. Le modèle est plus éloigné des valeurs aberrantes, mais plus proche de la plupart des autres points de données.
Testez vos connaissances
Prenons l'exemple des deux graphiques suivants d'un modèle linéaire ajusté à un ensemble de données :
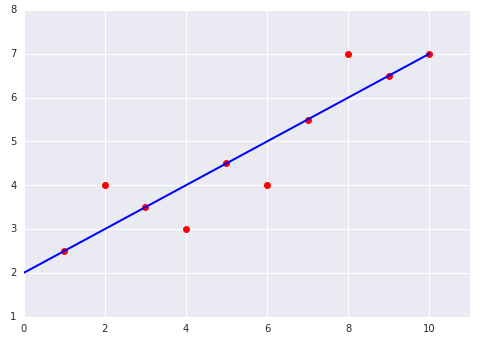
|
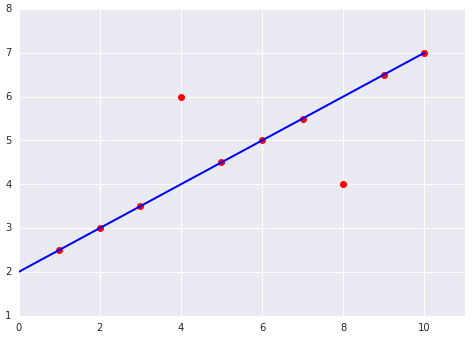
|
