Verlust ist ein numerischer Messwert, der beschreibt, wie falsch die Vorhersagen eines Modells sind. Der Verlust misst den Abstand zwischen den Vorhersagen des Modells und den tatsächlichen Labels. Ziel des Trainings eines Modells ist es, den Verlust zu minimieren und auf den niedrigstmöglichen Wert zu reduzieren.
Im folgenden Bild wird der Verlust als Pfeile dargestellt, die von den Datenpunkten zum Modell verlaufen. Die Pfeile zeigen, wie weit die Vorhersagen des Modells von den tatsächlichen Werten entfernt sind.
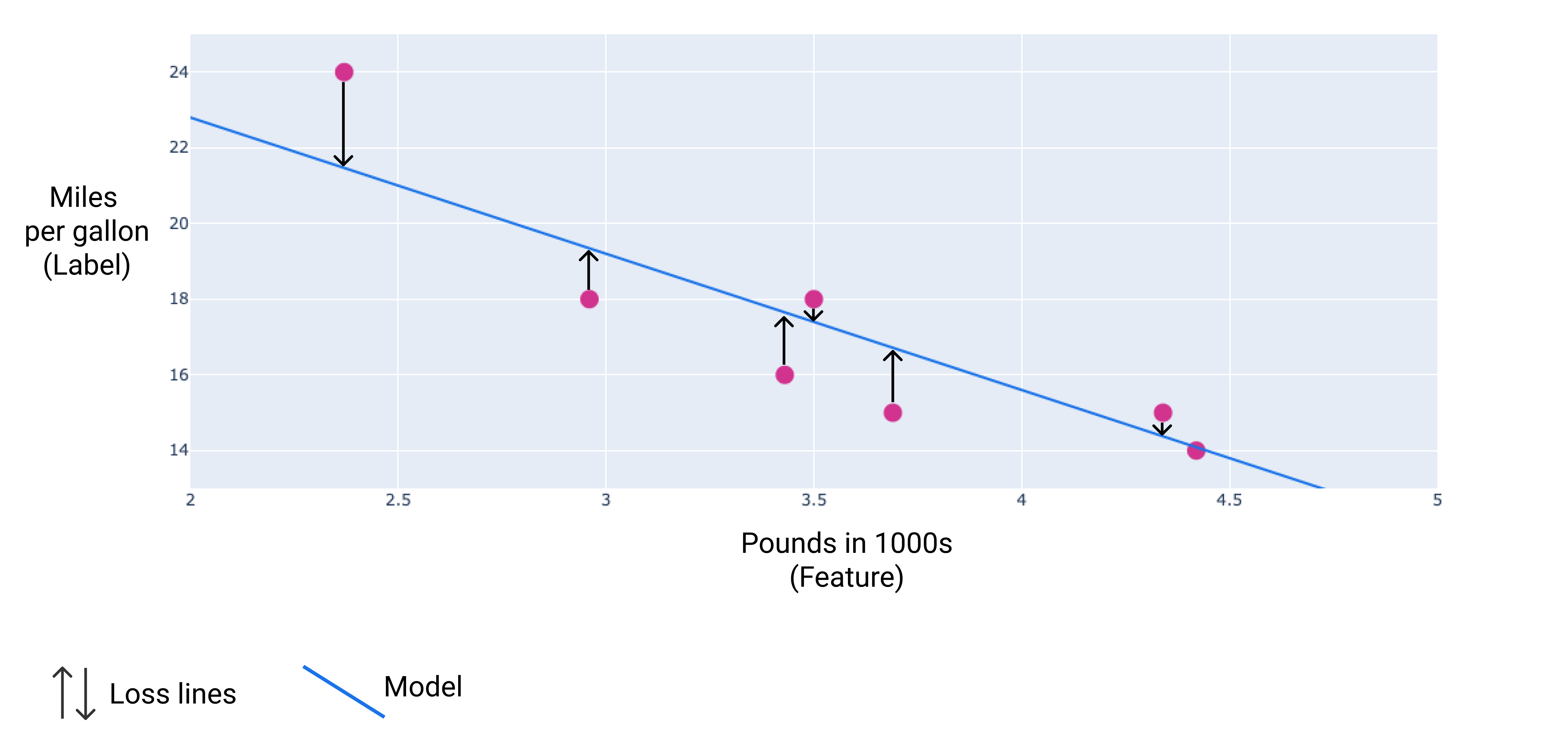
Abbildung 8. Der Verlust wird vom tatsächlichen Wert zum vorhergesagten Wert gemessen.
Entfernung des Verlusts
In der Statistik und beim maschinellen Lernen wird mit dem Verlust die Differenz zwischen den vorhergesagten und den tatsächlichen Werten gemessen. Bei Verlust wird der Abstand zwischen den Werten berücksichtigt, nicht die Richtung. Wenn ein Modell beispielsweise den Wert 2 vorhersagt, der tatsächliche Wert aber 5 ist, ist es uns egal, dass der Verlust negativ ist ($ 2-5=-3 $). Stattdessen ist uns wichtig, dass der Abstand zwischen den Werten $ 3$ beträgt. Daher wird bei allen Methoden zur Berechnung des Verlusts das Vorzeichen entfernt.
Die beiden gängigsten Methoden zum Entfernen des Zeichens sind:
- Bilden Sie den absoluten Wert der Differenz zwischen dem tatsächlichen Wert und der Vorhersage.
- Die Differenz zwischen dem tatsächlichen Wert und der Vorhersage wird quadriert.
Arten von Verlusten
Bei der linearen Regression gibt es fünf Haupttypen von Verlusten, die in der folgenden Tabelle aufgeführt sind.
| Verlusttyp | Definition | Gleichung |
|---|---|---|
| L1-Verlust | Die Summe der absoluten Werte der Differenz zwischen den vorhergesagten und den tatsächlichen Werten. | $ ∑ | actual\ value - predicted\ value | $ |
| Mittlerer absoluter Fehler (MAE) | Der Durchschnitt der L1-Verluste für eine Reihe von N Beispielen. | $ \frac{1}{N} ∑ | actual\ value - predicted\ value | $ |
| L2-Verlust | Die Summe der quadrierten Differenz zwischen den vorhergesagten und den tatsächlichen Werten. | $ ∑(actual\ value - predicted\ value)^2 $ |
| Mittlere quadratische Abweichung (MSE) | Der Durchschnitt der L2-Verluste für eine Reihe von N Beispielen. | $ \frac{1}{N} ∑ (actual\ value - predicted\ value)^2 $ |
| Wurzel der mittleren Fehlerquadratsumme (RMSE) | Die Quadratwurzel der mittleren quadratischen Abweichung (Mean Squared Error, MSE). | $ \sqrt{\frac{1}{N} ∑ (actual\ value - predicted\ value)^2} $ |
Der funktionale Unterschied zwischen L1-Verlust und L2-Verlust (oder zwischen MAE/RMSE und MSE) besteht in der Quadrierung. Wenn der Unterschied zwischen der Vorhersage und dem Label groß ist, wird der Verlust durch die Quadrierung noch größer. Wenn der Unterschied gering ist (weniger als 1), wird der Verlust durch die Quadrierung noch geringer.
Verlustmesswerte wie MAE und RMSE sind in einigen Anwendungsfällen möglicherweise dem L2-Verlust oder MSE vorzuziehen, da sie in der Regel besser nachvollziehbar sind. Sie messen den Fehler auf derselben Skala wie der vorhergesagte Wert des Modells.
Wenn Sie mehrere Beispiele gleichzeitig verarbeiten, empfehlen wir, die Verluste über alle Beispiele hinweg zu mitteln, unabhängig davon, ob Sie MAE, MSE oder RMSE verwenden.
Beispiel für die Berechnung des Verlusts
Anhand der vorherigen Best-Fit-Linie berechnen wir den L2-Verlust für ein einzelnes Beispiel. Aus der Linie der besten Anpassung ergaben sich die folgenden Werte für Gewicht und Bias:
- $ \small{Gewicht: -4,6} $
- $ \small{Bias: 34} $
Wenn das Modell vorhersagt, dass ein 1.075 kg schweres Auto 9,8 km pro Liter fährt, es aber tatsächlich 11,05 km pro Liter fährt, wird der L2-Verlust so berechnet:
| Wert | Gleichung | Ergebnis |
|---|---|---|
| Vorhersage | $\small{bias + (weight * feature\ value)}$ $\small{34 + (-4.6*2.37)}$ |
$\small{23.1}$ |
| Tatsächlicher Wert | $ \small{ label } $ | $ \small{ 26 } $ |
| L2-Verlust | $ \small{ (actual\ value - predicted\ value)^2 } $ $\small{ (26 - 23.1)^2 }$ |
$\small{8.41}$ |
In diesem Beispiel beträgt der L2-Verlust für diesen einzelnen Datenpunkt 8, 41.
Verlust auswählen
Die Entscheidung, ob MAE oder MSE verwendet werden soll, kann vom Dataset und der Art und Weise abhängen, wie Sie bestimmte Vorhersagen behandeln möchten. Die meisten Feature-Werte in einem Dataset liegen in der Regel in einem bestimmten Bereich. Autos wiegen beispielsweise normalerweise zwischen 900 und 2.250 kg und verbrauchen zwischen 1,9 und 11,8 l pro 100 km. Ein Auto mit einem Gewicht von 3.629 kg oder ein Auto,das 42,5 km pro Liter fährt, liegt außerhalb des typischen Bereichs und würde als Ausreißer betrachtet.
Ein Ausreißer kann sich auch darauf beziehen, wie weit die Vorhersagen eines Modells von den tatsächlichen Werten entfernt sind. Beispielsweise liegt ein Gewicht von 3.000 Pfund im typischen Bereich für das Gewicht von Autos und 40 Meilen pro Gallone im typischen Bereich für die Kraftstoffeffizienz. Ein 1.360 kg schweres Auto, das 17 km pro Liter fährt, wäre jedoch ein Ausreißer in Bezug auf die Vorhersage des Modells, da das Modell vorhersagen würde, dass ein 1.360 kg schweres Auto etwa 8,5 km pro Liter fährt.
Berücksichtigen Sie bei der Auswahl der besten Verlustfunktion, wie das Modell Ausreißer behandeln soll. Bei MSE wird das Modell beispielsweise stärker in Richtung der Ausreißer verschoben, bei MAE nicht. Der L2-Verlust führt zu einer viel höheren Strafe für einen Ausreißer als der L1-Verlust. Die folgenden Bilder zeigen beispielsweise ein mit MAE trainiertes Modell und ein mit MSE trainiertes Modell. Die rote Linie stellt ein vollständig trainiertes Modell dar, das für Vorhersagen verwendet wird. Die Ausreißer liegen näher am Modell, das mit MSE trainiert wurde, als am Modell, das mit MAE trainiert wurde.
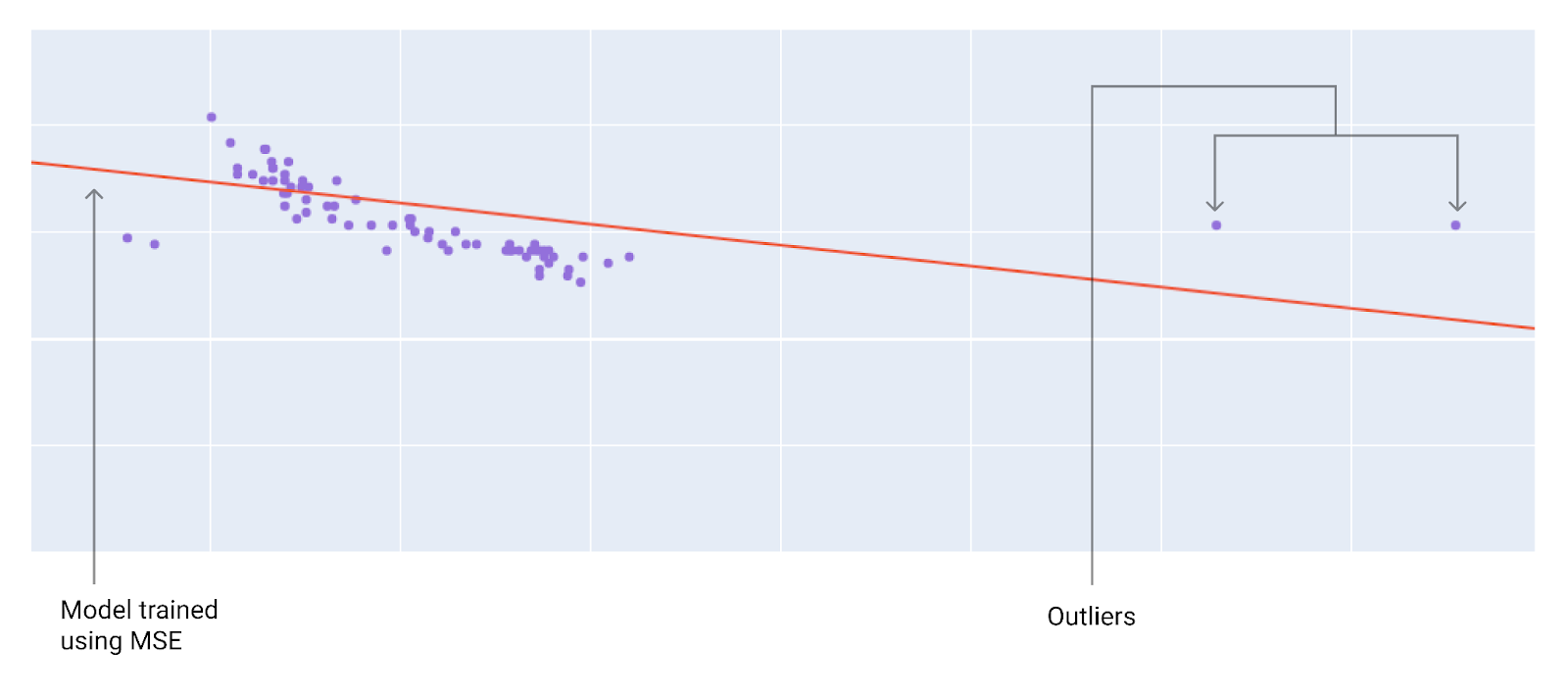
Abbildung 9. Durch den MSE-Verlust wird das Modell näher an die Ausreißer herangeführt.
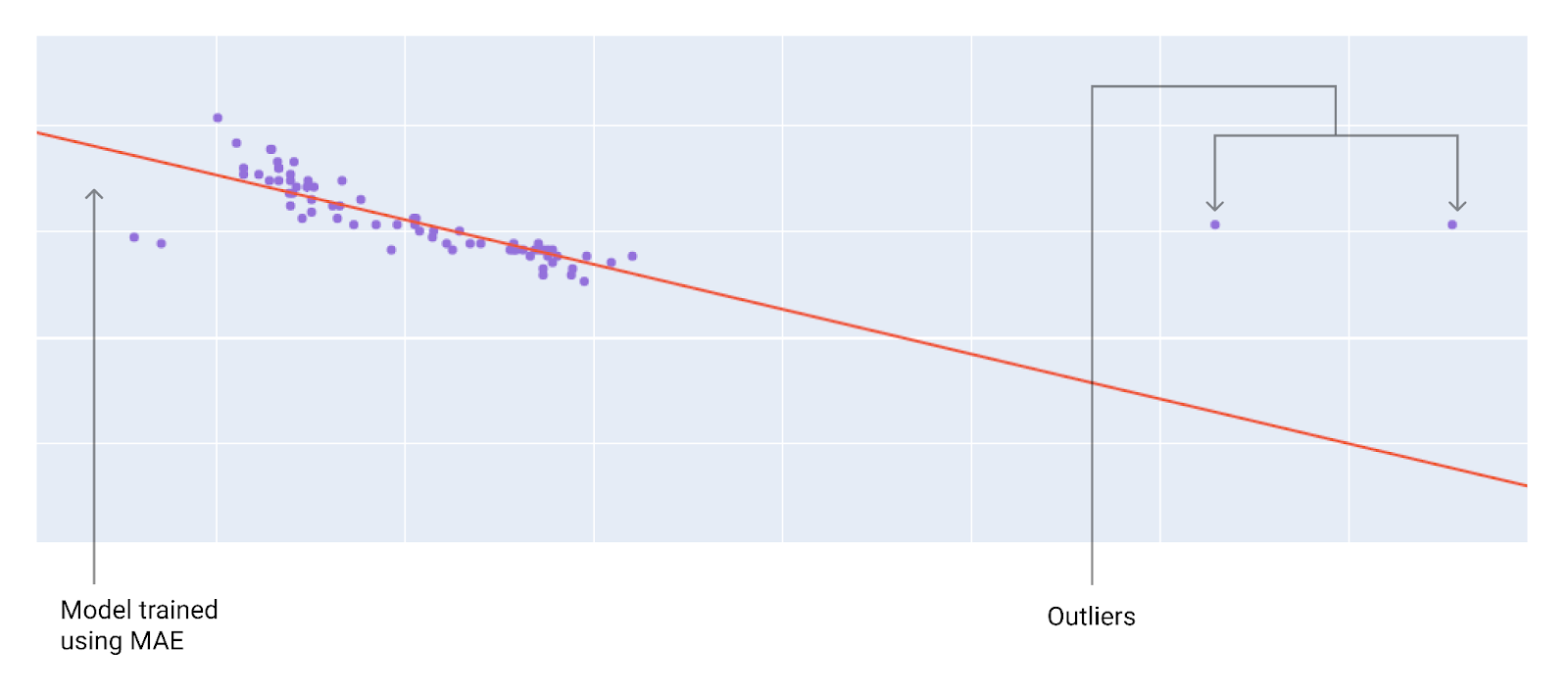
Abbildung 10. Durch den MAE-Verlust wird das Modell von den Ausreißern ferngehalten.
Beachten Sie die Beziehung zwischen dem Modell und den Daten:
MSE Das Modell liegt näher an den Ausreißern, aber weiter entfernt von den meisten anderen Datenpunkten.
MAE. Das Modell ist weiter von den Ausreißern entfernt, aber näher an den meisten anderen Datenpunkten.
Wissen testen
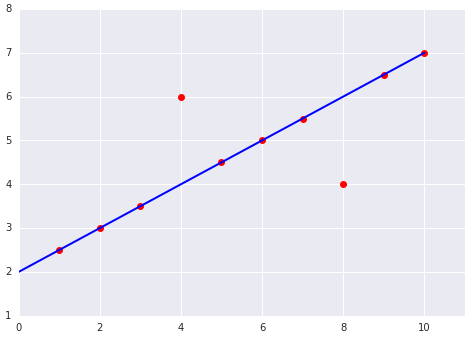
Sehen Sie sich die folgenden beiden Diagramme eines linearen Modells an, das an einen Datensatz angepasst wurde:
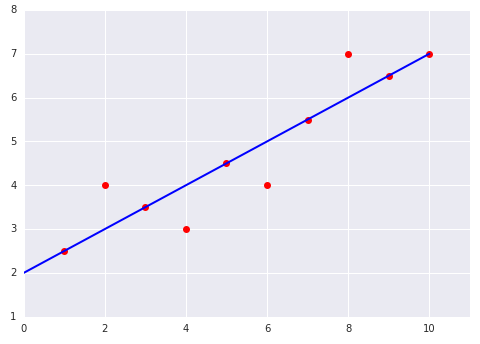
|
|
