Loss คือเมตริกเชิงตัวเลขที่อธิบายว่าการคาดการณ์ของโมเดลผิดพลาดมากน้อยเพียงใด การสูญเสียจะวัดระยะห่างระหว่างการคาดการณ์ของโมเดลกับป้ายกำกับจริง เป้าหมายของการฝึกโมเดลคือการลด Loss ให้น้อยที่สุด ซึ่งก็คือการลด Loss ให้เหลือค่าที่ต่ำที่สุดเท่าที่จะเป็นไปได้
ในรูปภาพต่อไปนี้ คุณจะเห็นภาพการสูญเสียเป็นลูกศรที่วาดจากจุดข้อมูลไปยังโมเดล ลูกศรแสดงให้เห็นว่าการคาดการณ์ของโมเดลอยู่ห่างจากค่าจริงมากน้อยเพียงใด
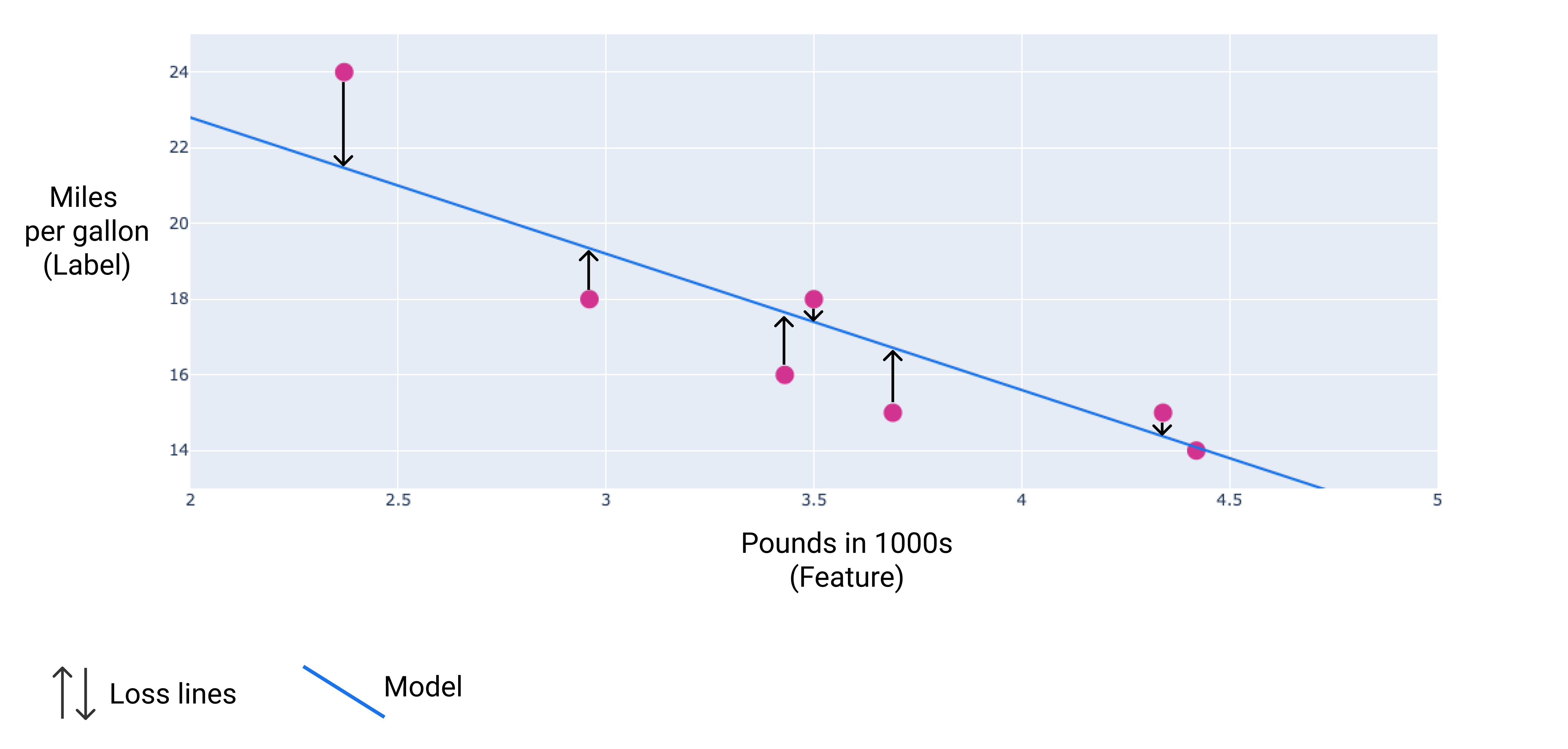
รูปที่ 8 การสูญเสียจะวัดจากค่าจริงไปยังค่าที่คาดการณ์
ระยะทางที่สูญเสีย
ในสถิติและแมชชีนเลิร์นนิง การสูญเสียจะวัดความแตกต่างระหว่างค่าที่คาดการณ์และค่าจริง Loss จะเน้นที่ระยะห่างระหว่างค่า ไม่ใช่ทิศทาง ตัวอย่างเช่น หากโมเดลคาดการณ์เป็น 2 แต่ค่าจริงคือ 5 เราไม่สนใจว่าการสูญเสียจะเป็นค่าลบ ($ 2-5=-3 $) แต่เราสนใจว่าระยะห่างระหว่างค่าคือ $ 3 $ ดังนั้นวิธีการทั้งหมด ในการคำนวณการสูญเสียจึงนำเครื่องหมายออก
2 วิธีที่พบบ่อยที่สุดในการนำลายเซ็นออกมีดังนี้
- ใช้ค่าสัมบูรณ์ของความแตกต่างระหว่างค่าจริงกับค่าที่คาดการณ์
- ยกกำลังสองความแตกต่างระหว่างค่าจริงกับการคาดการณ์
ประเภทของการสูญเสีย
ในการถดถอยเชิงเส้น การสูญเสียมี 5 ประเภทหลัก ซึ่งสรุปไว้ในตารางต่อไปนี้
| ประเภทการสูญเสีย | คำจำกัดความ | สมการ |
|---|---|---|
| การสูญเสีย L1 | ผลรวมของค่าสัมบูรณ์ของความแตกต่าง ระหว่างค่าที่คาดการณ์กับค่าจริง | $ ∑ | ค่าจริง - ค่าที่คาดการณ์ | $ |
| ค่าเฉลี่ยความคลาดเคลื่อนสัมบูรณ์ (MAE) | ค่าเฉลี่ยของความสูญเสีย L1 ในชุดตัวอย่าง N | $ \frac{1}{N} ∑ | ค่าจริง - ค่าที่คาดการณ์ | $ |
| L2 loss | ผลรวมของผลต่างกำลังสอง ระหว่างค่าที่คาดการณ์และค่าจริง | $ ∑(ค่าจริง - ค่าที่คาดการณ์)^2 $ |
| ความคลาดเคลื่อนเฉลี่ยกำลังสอง (MSE) | ค่าเฉลี่ยของความสูญเสีย L2 ในชุดตัวอย่าง N | $ \frac{1}{N} ∑ (actual\ value - predicted\ value)^2 $ |
| ค่าเฉลี่ยความคลาดเคลื่อนกำลังสอง (RMSE) | สแควรูทของความคลาดเคลื่อนเฉลี่ยกำลังสอง (MSE) | $ \sqrt{\frac{1}{N} ∑ (actual\ value - predicted\ value)^2} $ |
ความแตกต่างด้านฟังก์ชันระหว่างการสูญเสีย L1 กับการสูญเสีย L2 (หรือระหว่าง MAE/RMSE กับ MSE) คือการยกกำลังสอง เมื่อความแตกต่างระหว่างการคาดการณ์กับป้ายกำกับมีค่ามาก การยกกำลังสองจะทำให้ค่า Loss มากยิ่งขึ้น เมื่อความแตกต่างมีน้อย (น้อยกว่า 1) การยกกำลังสองจะทำให้การสูญเสียยิ่งน้อยลง
เมตริกการสูญเสีย เช่น MAE และ RMSE อาจดีกว่าการสูญเสีย L2 หรือ MSE ใน บางกรณีการใช้งาน เนื่องจากมักจะตีความได้ง่ายกว่า เพราะเมตริกเหล่านี้วัด ข้อผิดพลาดโดยใช้มาตราส่วนเดียวกับค่าที่โมเดลคาดการณ์ไว้
เมื่อประมวลผลตัวอย่างหลายรายการพร้อมกัน เราขอแนะนำให้หาค่าเฉลี่ยของค่าสูญเสีย ในตัวอย่างทั้งหมด ไม่ว่าจะใช้ MAE, MSE หรือ RMSE
ตัวอย่างการคำนวณการสูญเสีย
เราจะคำนวณการสูญเสีย L2 สำหรับตัวอย่างเดียวโดยใช้เส้นที่เหมาะสมที่สุดก่อนหน้า จาก เส้นที่เหมาะสมที่สุด เราได้ค่าต่อไปนี้สำหรับน้ำหนักและอคติ
- $ \small{Weight: -4.6} $
- $ \small{Bias: 34} $
หากโมเดลคาดการณ์ว่ารถยนต์หนัก 2,370 ปอนด์วิ่งได้ 23.1 ไมล์ต่อแกลลอน แต่ในความเป็นจริงวิ่งได้ 26 ไมล์ต่อแกลลอน เราจะคำนวณค่า Loss 2 ดังนี้
| ค่า | สมการ | ผลลัพธ์ |
|---|---|---|
| การคาดการณ์ | $\small{bias + (weight * feature\ value)}$ $\small{34 + (-4.6*2.37)}$ |
$\small{23.1}$ |
| มูลค่าที่แท้จริง | $ \small{ label } $ | $ \small{ 26 } $ |
| การสูญเสีย L2 | $ \small{ (ค่าจริง - ค่าที่คาดการณ์)^2 } $ $\small{ (26 - 23.1)^2 }$ |
$\small{8.41}$ |
ในตัวอย่างนี้ การสูญเสีย L2 สำหรับจุดข้อมูลเดียวคือ 8.41
การเลือกการสูญเสีย
การตัดสินใจว่าจะใช้ MAE หรือ MSE อาจขึ้นอยู่กับชุดข้อมูลและวิธีที่คุณ ต้องการจัดการการคาดการณ์บางอย่าง โดยปกติแล้ว ค่าฟีเจอร์ส่วนใหญ่ในชุดข้อมูลจะ อยู่ในช่วงที่แตกต่างกัน เช่น โดยปกติแล้วรถยนต์จะมีน้ำหนักระหว่าง 2,000 ถึง 5,000 ปอนด์ และวิ่งได้ระหว่าง 8 ถึง 50 ไมล์ต่อแกลลอน รถยนต์ที่มีน้ำหนัก 8,000 ปอนด์ หรือรถยนต์ที่วิ่งได้ 100 ไมล์ต่อแกลลอนอยู่นอกช่วงปกติและถือเป็นค่าผิดปกติ
ค่าผิดปกติยังหมายถึงความคลาดเคลื่อนของการคาดการณ์ของโมเดลจากค่าจริงได้ด้วย เช่น 3,000 ปอนด์อยู่ในช่วงน้ำหนักรถยนต์ทั่วไป และ 40 ไมล์ต่อแกลลอนอยู่ในช่วงประสิทธิภาพการใช้เชื้อเพลิงทั่วไป อย่างไรก็ตาม รถยนต์หนัก 3,000 ปอนด์ที่วิ่งได้ 40 ไมล์ต่อแกลลอนจะเป็นค่าผิดปกติในแง่ของการคาดการณ์ของโมเดล เนื่องจากโมเดลจะคาดการณ์ว่ารถยนต์หนัก 3,000 ปอนด์จะวิ่งได้ประมาณ 20 ไมล์ต่อแกลลอน
เมื่อเลือกฟังก์ชันการสูญเสียที่ดีที่สุด ให้พิจารณาว่าคุณต้องการให้โมเดลจัดการกับค่าผิดปกติอย่างไร เช่น MSE จะย้ายโมเดลไปทางค่าที่ผิดปกติมากขึ้น ในขณะที่ MAE จะไม่ทำ การสูญเสีย L2 จะทำให้เกิดค่าปรับที่สูงกว่ามากสำหรับค่าผิดปกติเมื่อเทียบกับการสูญเสีย L1 ตัวอย่างเช่น รูปภาพต่อไปนี้แสดงโมเดลที่ฝึก โดยใช้ MAE และโมเดลที่ฝึกโดยใช้ MSE เส้นสีแดงแสดงถึงโมเดลที่ได้รับการฝึกอย่างเต็มที่ ซึ่งจะใช้ในการคาดการณ์ ค่าที่ผิดปกติจะอยู่ใกล้กับ โมเดลที่ฝึกด้วย MSE มากกว่าโมเดลที่ฝึกด้วย MAE
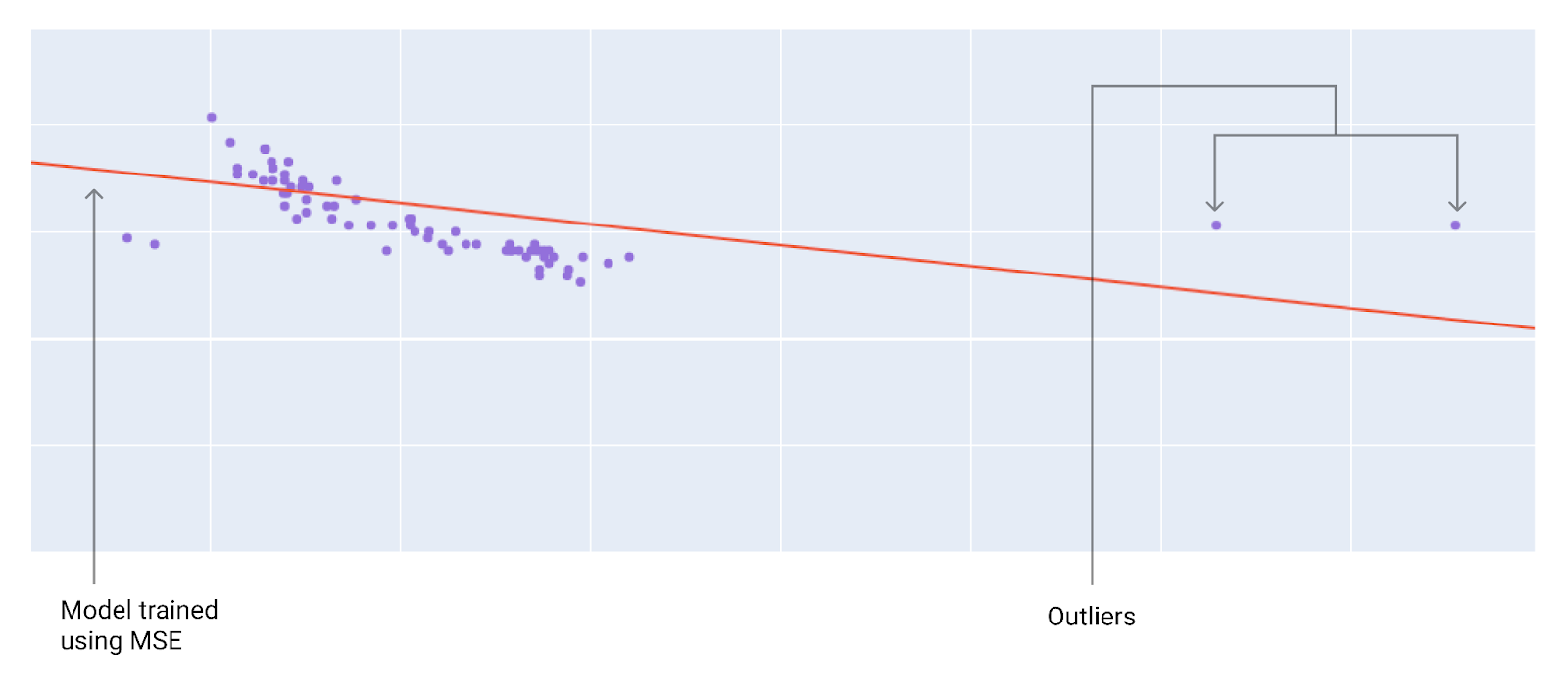
รูปที่ 9 การสูญเสีย MSE จะทำให้โมเดลเข้าใกล้ค่าผิดปกติมากขึ้น
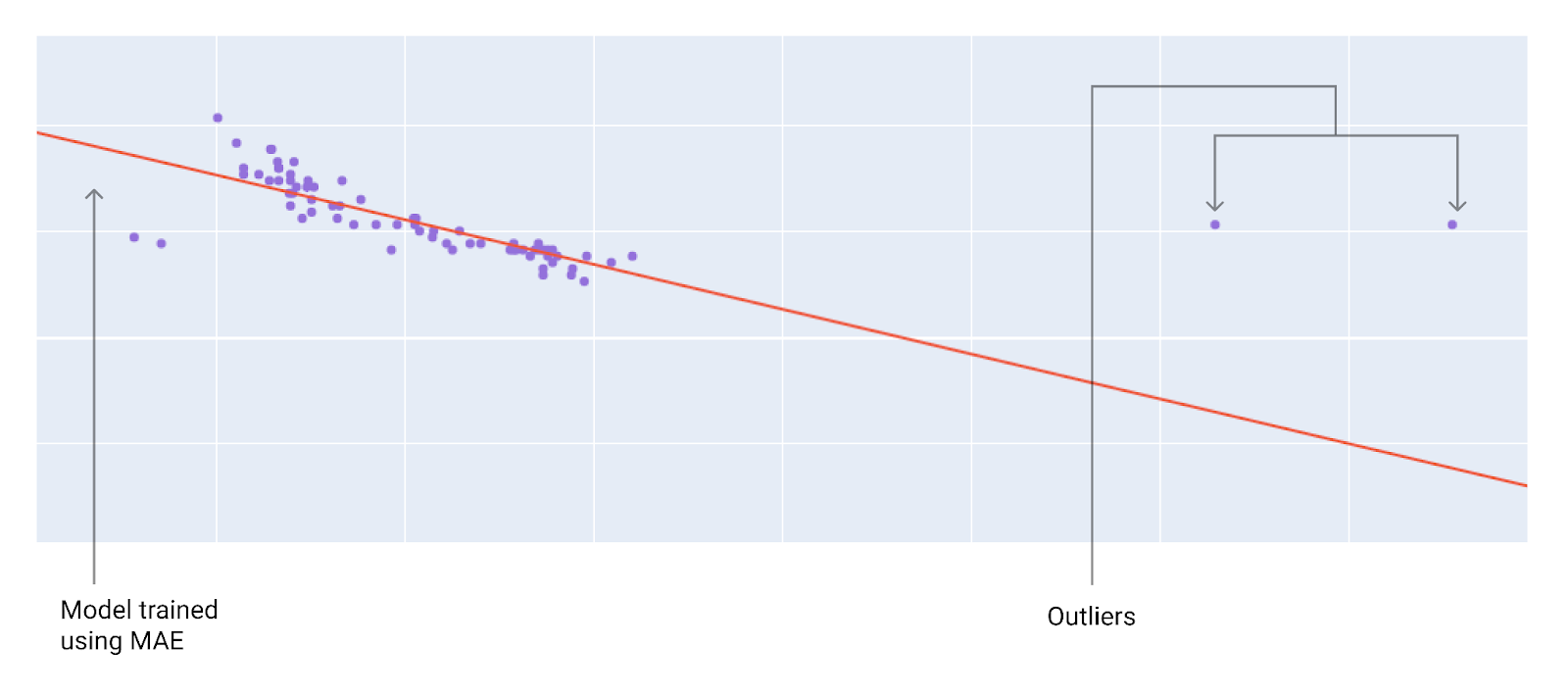
รูปที่ 10 การสูญเสีย MAE จะทำให้โมเดลอยู่ห่างจากค่าที่ผิดปกติมากขึ้น
โปรดทราบความสัมพันธ์ระหว่างโมเดลกับข้อมูล
MSE โมเดลอยู่ใกล้ค่าที่ผิดปกติมากกว่า แต่ไกลจากจุดข้อมูลอื่นๆ ส่วนใหญ่
MAE โมเดลอยู่ห่างจากค่าที่ผิดปกติมากขึ้น แต่ใกล้กับจุดข้อมูลอื่นๆ ส่วนใหญ่มากขึ้น
ทดสอบความเข้าใจ
พิจารณากราฟ 2 กราฟต่อไปนี้ของโมเดลเชิงเส้นที่ปรับให้เข้ากับชุดข้อมูล
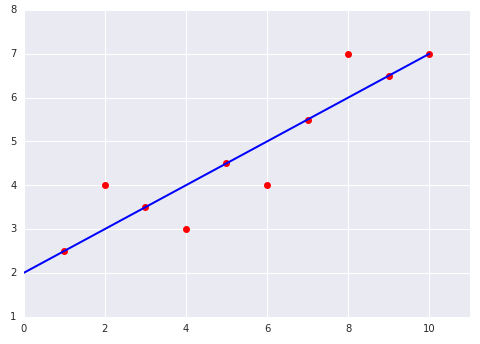
|
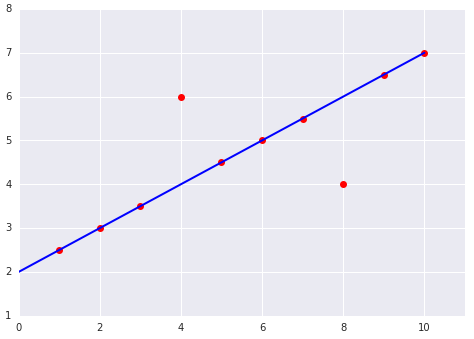
|
