Mất mát là một chỉ số bằng số mô tả mức độ sai lệch của dự đoán của một mô hình. Mất mát đo lường khoảng cách giữa các dự đoán của mô hình và nhãn thực tế. Mục tiêu của việc huấn luyện mô hình là giảm thiểu tổn thất, giảm xuống giá trị thấp nhất có thể.
Trong hình ảnh sau, bạn có thể hình dung tổn thất dưới dạng các mũi tên được vẽ từ các điểm dữ liệu đến mô hình. Các mũi tên cho biết mức độ chênh lệch giữa kết quả dự đoán của mô hình và giá trị thực tế.
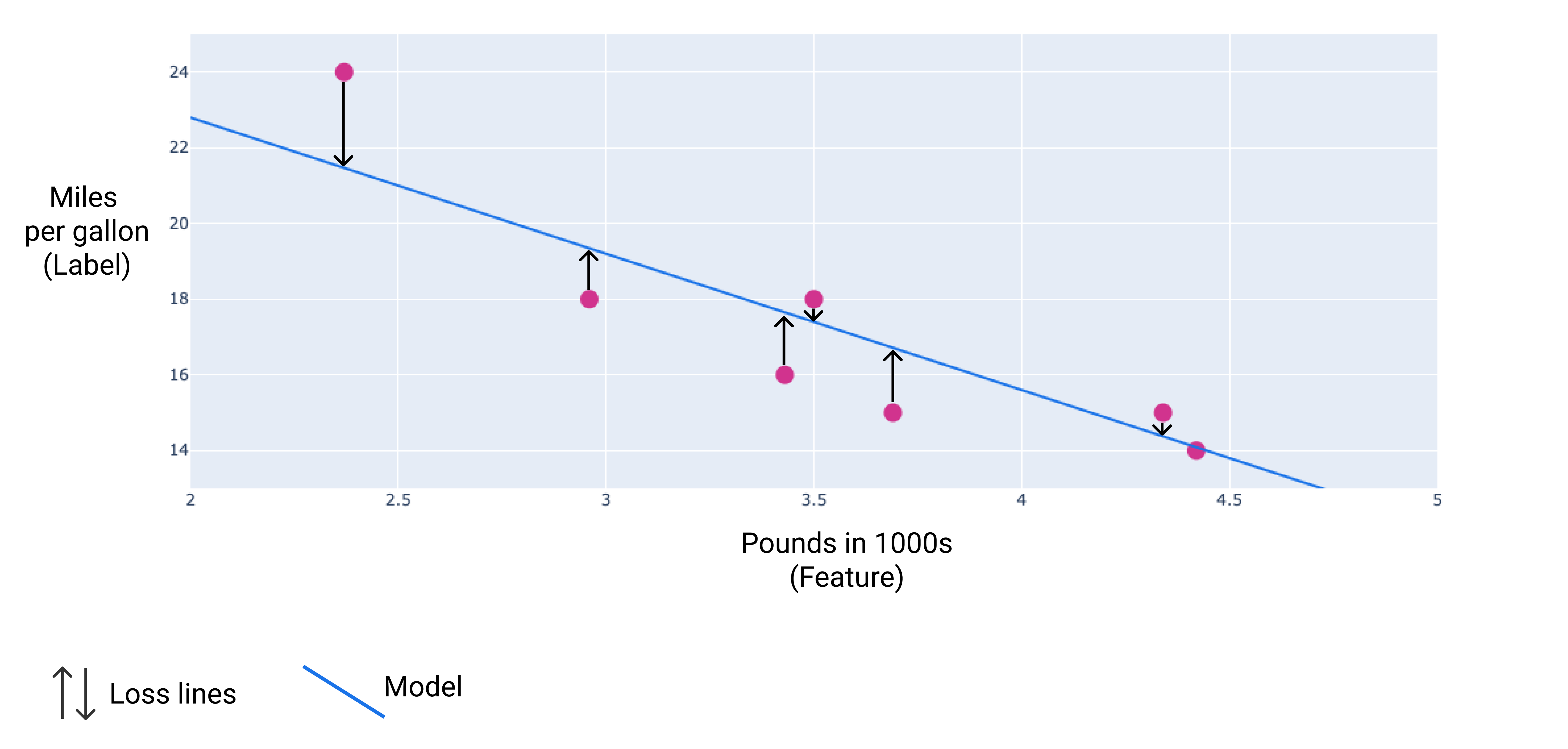
Hình 8. Mức tổn thất được đo từ giá trị thực tế đến giá trị dự đoán.
Khoảng cách mất tín hiệu
Trong thống kê và học máy, tổn thất đo lường sự khác biệt giữa giá trị dự đoán và giá trị thực tế. Hàm mất mát tập trung vào khoảng cách giữa các giá trị, chứ không phải hướng. Ví dụ: nếu một mô hình dự đoán là 2, nhưng giá trị thực tế là 5, thì chúng ta không quan tâm đến việc tổn thất là âm (2 – 5= –3). Thay vào đó, chúng ta quan tâm đến khoảng cách giữa các giá trị là 3. Do đó, tất cả các phương pháp tính toán tổn thất đều loại bỏ dấu.
Sau đây là 2 phương pháp phổ biến nhất để xoá biển báo:
- Lấy giá trị tuyệt đối của mức chênh lệch giữa giá trị thực tế và giá trị dự đoán.
- Bình phương sự khác biệt giữa giá trị thực tế và giá trị dự đoán.
Các loại tổn thất
Trong hồi quy tuyến tính, có 5 loại tổn thất chính được trình bày trong bảng sau.
| Loại tổn thất | Định nghĩa | Phương trình |
|---|---|---|
| MấtL1 | Tổng giá trị tuyệt đối của độ chênh lệch giữa giá trị dự đoán và giá trị thực tế. | $ ∑ | giá\ trị\ thực\ tế – giá\ trị\ dự\ đoán | $ |
| Sai số tuyệt đối trung bình (MAE) | Giá trị trung bình của các tổn thất L1 trên một tập hợp gồm N ví dụ. | $ \frac{1}{N} ∑ | giá\ trị\ thực\ tế - giá\ trị\ dự\ đoán | $ |
| Mất mát L2 | Tổng của bình phương hiệu số giữa các giá trị dự đoán và giá trị thực tế. | $ ∑(giá\ trị\ thực\ tế – giá\ trị\ dự\ đoán)^2 $ |
| Sai số bình phương trung bình (MSE) | Giá trị trung bình của tổn thất L2 trên một tập hợp gồm N ví dụ. | $ \frac{1}{N} ∑ (giá\ trị\ thực\ tế - giá\ trị\ dự\ đoán)^2 $ |
| Sai số trung bình bình phương (RMSE) | Căn bậc hai của sai số bình phương trung bình (MSE). | $ \sqrt{\frac{1}{N} ∑ (giá\ trị\ thực\ tế - giá\ trị\ dự\ đoán)^2} $ |
Sự khác biệt về chức năng giữa tổn thất L1 và tổn thất L2 (hoặc giữa MAE/RMSE và MSE) là bình phương. Khi có sự khác biệt lớn giữa dự đoán và nhãn, việc bình phương sẽ khiến tổn thất lớn hơn nữa. Khi sự khác biệt nhỏ (dưới 1), việc bình phương sẽ làm cho tổn thất nhỏ hơn nữa.
Các chỉ số tổn thất như MAE và RMSE có thể được ưu tiên hơn tổn thất L2 hoặc MSE trong một số trường hợp sử dụng vì chúng có xu hướng dễ được con người diễn giải hơn, vì chúng đo lường lỗi bằng cách sử dụng cùng một thang đo với giá trị dự đoán của mô hình.
Khi xử lý nhiều ví dụ cùng một lúc, bạn nên tính trung bình các tổn thất trên tất cả các ví dụ, cho dù sử dụng MAE, MSE hay RMSE.
Ví dụ về cách tính tổn thất
Trong phần trước, chúng ta đã tạo mô hình sau đây để dự đoán mức tiêu thụ nhiên liệu dựa trên trọng lượng của ô tô:
- Mô hình: $ y' = 34 + (-4.6)(x_1) $
- Trọng số: $ –4,6 $
- Độ lệch: 34 USD
Nếu mô hình dự đoán rằng một chiếc ô tô nặng 2.370 pound sẽ đi được 23,1 dặm/gallon, nhưng thực tế là 24 dặm/gallon, thì chúng ta sẽ tính mức tổn thất L2 như sau:
| Giá trị | Phương trình | Kết quả |
|---|---|---|
| Dự đoán | $\small{bias + (weight * feature\ value)}$ $\small{34 + (-4.6*2.37)}$ |
$\small{23.1}$ |
| Giá trị thực tế | $ \small{ label } $ | $ \small{ 24 } $ |
| Tổn thất L2 | $ \small{ (giá\ trị\ thực\ tế - giá\ trị\ dự\ đoán)^2 } $ $\small{ (24 - 23,1)^2 }$ |
$\small{0,81}$ |
Trong ví dụ này, tổn thất L2 cho điểm dữ liệu duy nhất đó là 0,81.
Chọn một trận thua
Việc quyết định sử dụng MAE hay MSE có thể phụ thuộc vào tập dữ liệu và cách bạn muốn xử lý một số dự đoán nhất định. Hầu hết các giá trị của đối tượng trong một tập dữ liệu thường nằm trong một dải ô riêng biệt. Ví dụ: ô tô thường có trọng lượng từ 2.000 đến 5.000 pound và đi được từ 8 đến 50 dặm cho mỗi gallon. Một chiếc ô tô nặng 8.000 pound hoặc một chiếc ô tô đi được 100 dặm/gallon nằm ngoài phạm vi thông thường và sẽ được coi là giá trị ngoại lệ.
Giá trị ngoại lệ cũng có thể đề cập đến mức độ chênh lệch giữa kết quả dự đoán của một mô hình với giá trị thực. Ví dụ: 3.000 pound nằm trong phạm vi trọng lượng xe thông thường và 40 dặm/gallon nằm trong phạm vi hiệu suất nhiên liệu thông thường. Tuy nhiên, một chiếc ô tô nặng 3.000 pound và đi được 40 dặm/gallon sẽ là một giá trị ngoại lệ về dự đoán của mô hình vì mô hình sẽ dự đoán rằng một chiếc ô tô nặng 3.000 pound sẽ đi được khoảng 20 dặm/gallon.
Khi chọn hàm tổn thất phù hợp nhất, hãy cân nhắc cách bạn muốn mô hình xử lý các giá trị ngoại lệ. Ví dụ: MSE di chuyển mô hình nhiều hơn về phía giá trị ngoại lệ, trong khi MAE thì không. Thua lỗ L2 sẽ phải chịu mức phạt cao hơn nhiều so với thua lỗ L1 đối với giá trị ngoại lai. Ví dụ: các hình ảnh sau đây cho thấy một mô hình được huấn luyện bằng MAE và một mô hình được huấn luyện bằng MSE. Đường màu đỏ biểu thị một mô hình được huấn luyện đầy đủ sẽ được dùng để đưa ra dự đoán. Các giá trị ngoại lệ gần với mô hình được huấn luyện bằng MSE hơn là mô hình được huấn luyện bằng MAE.
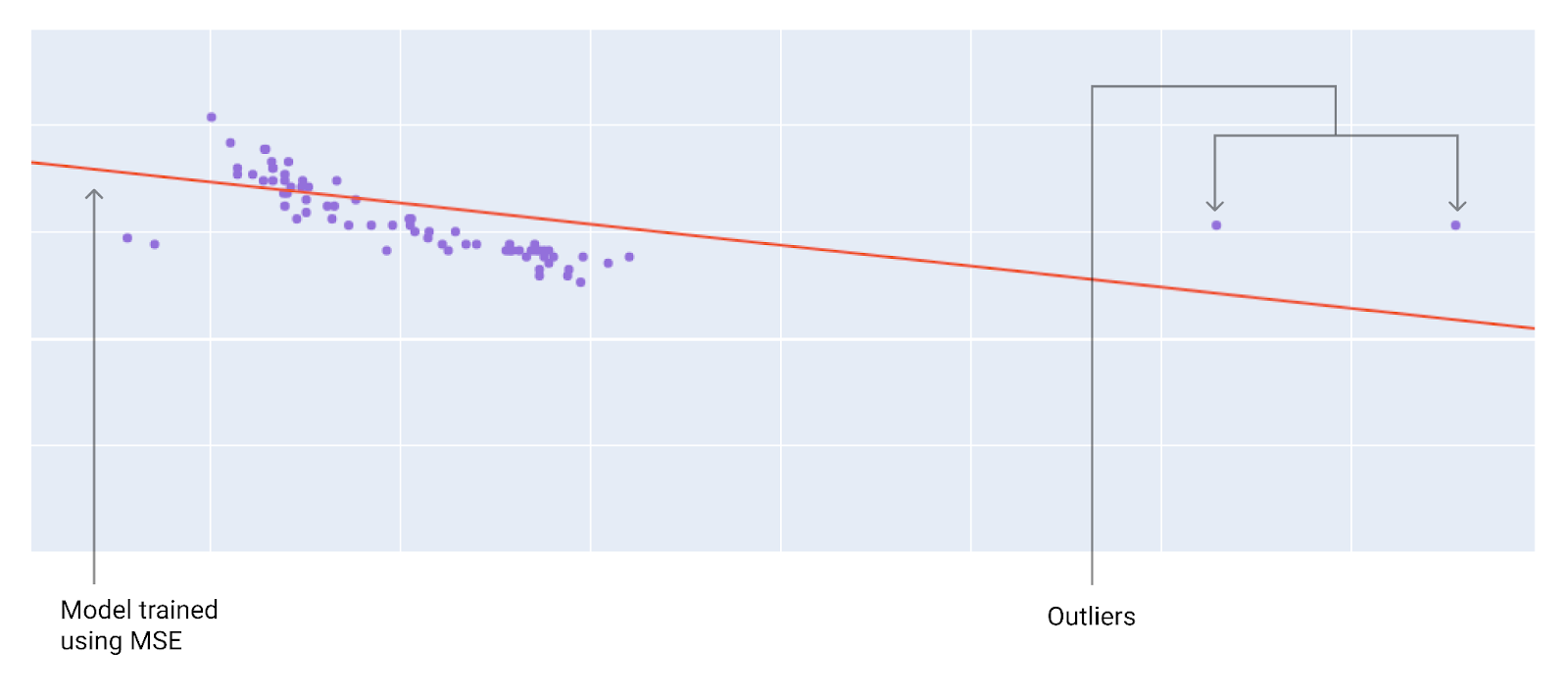
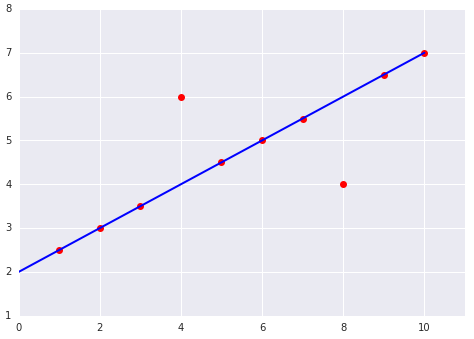
Hình 9. Mất mát MSE khiến mô hình gần với các giá trị ngoại lệ hơn.
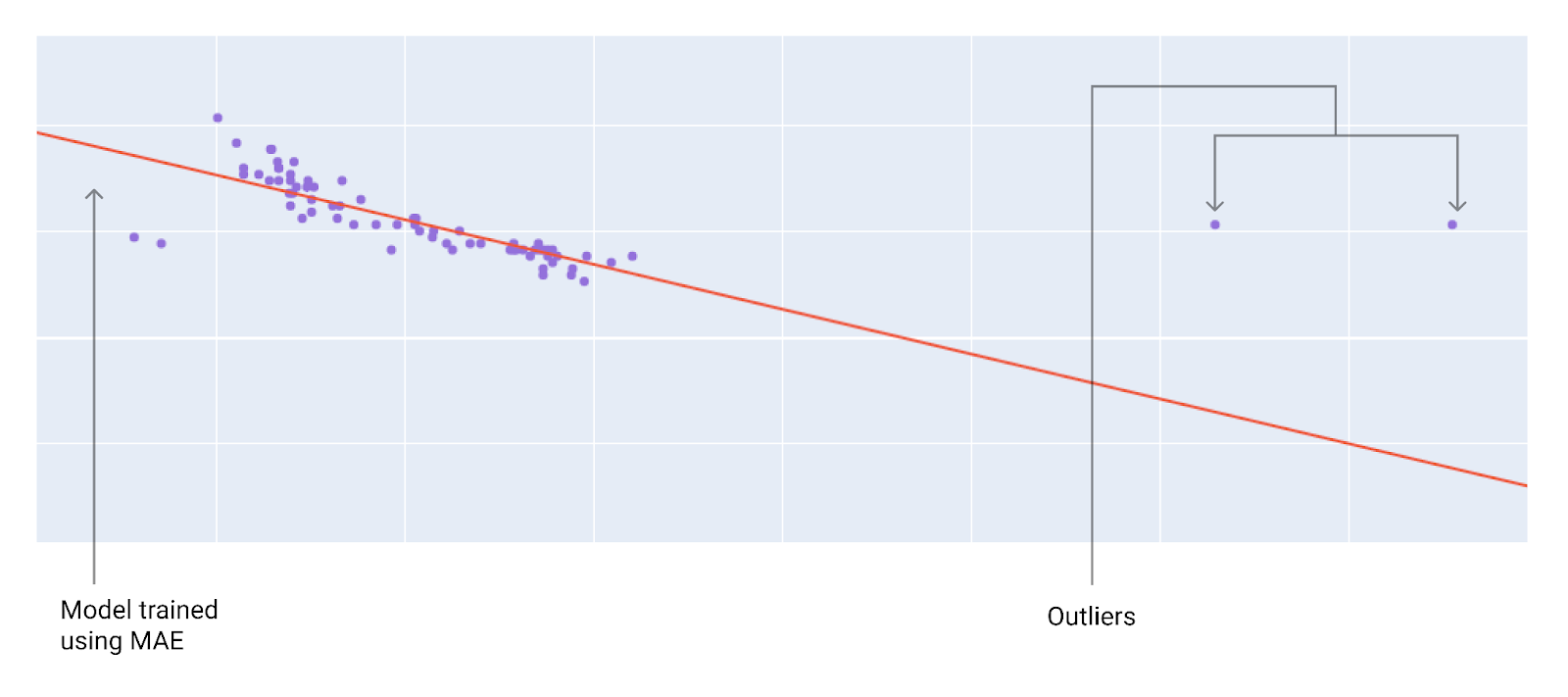
Hình 10. Mất mát MAE giúp mô hình tránh xa các giá trị ngoại lệ.
Lưu ý mối quan hệ giữa mô hình và dữ liệu:
MSE. Mô hình này gần với các giá trị ngoại lệ nhưng lại cách xa hầu hết các điểm dữ liệu khác.
MAE. Mô hình này nằm xa các giá trị ngoại lệ hơn nhưng gần với hầu hết các điểm dữ liệu khác.
Kiểm tra mức độ hiểu biết của bạn
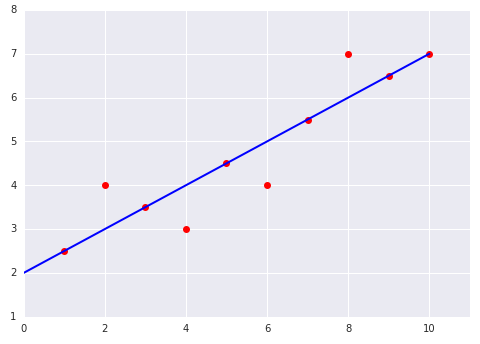
Hãy xem xét 2 biểu đồ sau đây của một mô hình tuyến tính phù hợp với một tập dữ liệu:
|
|
