लॉस एक संख्यात्मक मेट्रिक है. इससे यह पता चलता है कि मॉडल के अनुमान कितने गलत हैं. लॉस, मॉडल के अनुमानों और असल लेबल के बीच की दूरी को मापता है. किसी मॉडल को ट्रेन करने का मकसद, नुकसान को कम करना होता है. इसे कम से कम वैल्यू तक ले जाना होता है.
यहां दी गई इमेज में, डेटा पॉइंट से मॉडल तक खींचे गए ऐरो के तौर पर नुकसान को विज़ुअलाइज़ किया जा सकता है. तीरों से पता चलता है कि मॉडल के अनुमान, असल वैल्यू से कितने दूर हैं.
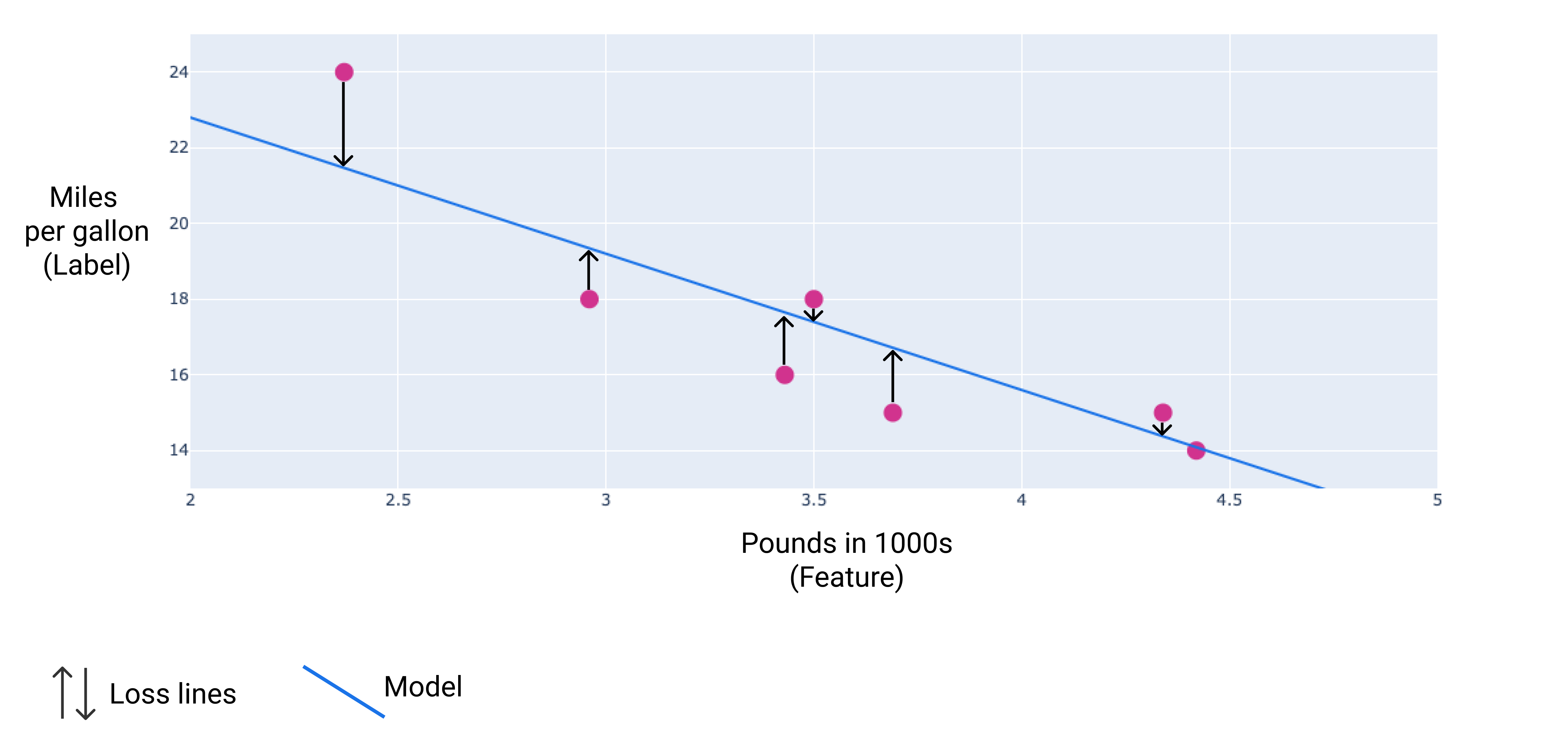
आठवीं इमेज. नुकसान का आकलन, असल वैल्यू से लेकर अनुमानित वैल्यू तक किया जाता है.
सिग्नल कमज़ोर होने की दूरी
आंकड़ों और मशीन लर्निंग में, लॉस से अनुमानित और असल वैल्यू के बीच के अंतर का पता चलता है. लॉस, वैल्यू के बीच की दूरी पर फ़ोकस करता है, न कि दिशा पर. उदाहरण के लिए, अगर कोई मॉडल 2 का अनुमान लगाता है, लेकिन असल वैल्यू 5 है, तो हमें इस बात से कोई फ़र्क़ नहीं पड़ता कि नुकसान नेगेटिव है (2 – 5= –3). इसके बजाय, हमें इस बात से मतलब है कि वैल्यू के बीच की दूरी 3 है. इसलिए, नुकसान का हिसाब लगाने के सभी तरीकों में से, साइन हटा दिया जाता है.
साइन हटाने के दो सबसे सामान्य तरीके यहां दिए गए हैं:
- असल वैल्यू और अनुमान के बीच के अंतर की ऐब्सलूट वैल्यू लें.
- असल वैल्यू और अनुमान के बीच के अंतर का स्क्वेयर करें.
नुकसान के टाइप
लीनियर रिग्रेशन में, पांच मुख्य तरह के लॉस होते हैं. इनके बारे में यहाँ दी गई टेबल में बताया गया है.
| नुकसान किस तरह का है | परिभाषा | समीकरण |
|---|---|---|
| L1 loss | अनुमानित वैल्यू और असल वैल्यू के बीच के अंतर की ऐब्सलूट वैल्यू का योग. | $ ∑ | actual\ value - predicted\ value | $ |
| मीन ऐब्सॉल्यूट एरर (एमएई) | N उदाहरणों के सेट में, L1 लॉस का औसत. | $ \frac{1}{N} ∑ | actual\ value - predicted\ value | $ |
| L2 loss | अनुमानित वैल्यू और असल वैल्यू के बीच के स्क्वेयर डिफ़रेंस का योग. | $ ∑(actual\ value - predicted\ value)^2 $ |
| मीन स्क्वेयर्ड एरर (एमएसई) | N उदाहरणों के सेट में, L2 लॉस का औसत. | $ \frac{1}{N} ∑ (actual\ value - predicted\ value)^2 $ |
| रूट मीन स्क्वेयर्ड एरर (आरएमएसई) | यह, मीन स्क्वेयर्ड एरर (एमएसई) का वर्गमूल होता है. | $ \sqrt{\frac{1}{N} ∑ (actual\ value - predicted\ value)^2} $ |
L1 लॉस और L2 लॉस (या MAE/RMSE और MSE) के बीच फ़ंक्शनल अंतर स्क्वेयरिंग है. जब अनुमान और लेबल के बीच का अंतर ज़्यादा होता है, तो स्क्वेयर करने से नुकसान और भी बढ़ जाता है. जब अंतर कम होता है (एक से कम), तो स्क्वेयर करने से नुकसान और भी कम हो जाता है.
कुछ मामलों में, MAE और RMSE जैसी लॉस मेट्रिक, L2 लॉस या MSE से बेहतर हो सकती हैं. ऐसा इसलिए, क्योंकि इन्हें समझना आसान होता है. साथ ही, ये मॉडल की अनुमानित वैल्यू के स्केल का इस्तेमाल करके, गड़बड़ी को मेज़र करती हैं.
एक साथ कई उदाहरणों को प्रोसेस करते समय, हमारा सुझाव है कि सभी उदाहरणों के लिए लॉस का औसत निकालें. भले ही, MAE, MSE या RMSE का इस्तेमाल किया जा रहा हो.
नुकसान का हिसाब लगाने का उदाहरण
पिछले सेक्शन में, हमने कार के वज़न के आधार पर, ईंधन की खपत का अनुमान लगाने के लिए यह मॉडल बनाया था:
- मॉडल: $ y' = 34 + (-4.6)(x_1) $
- वज़न: $ –4.6 $
- पूर्वाग्रह: $ 34 $
अगर मॉडल का अनुमान है कि 2,370 पाउंड की कार 23.1 मील प्रति गैलन का माइलेज देती है, लेकिन असल में वह 24 मील प्रति गैलन का माइलेज देती है, तो हम L2 लॉस का हिसाब इस तरह लगाएंगे:
| मान | समीकरण | नतीजा |
|---|---|---|
| अनुमान | $\small{bias + (weight * feature\ value)}$ $\small{34 + (-4.6*2.37)}$ |
$\small{23.1}$ |
| वास्तविक मान | $ \small{ label } $ | $ \small{ 24 } $ |
| L2 नुकसान | $ \small{ (actual\ value - predicted\ value)^2 } $ $\small{ (24 - 23.1)^2 }$ |
$\small{0.81}$ |
इस उदाहरण में, उस एक डेटा पॉइंट के लिए L2 लॉस 0.81 है.
नुकसान का विकल्प चुनना
डेटासेट और कुछ अनुमानों को हैंडल करने के तरीके के आधार पर, यह तय किया जा सकता है कि MAE या MSE का इस्तेमाल करना है या नहीं. किसी डेटासेट में ज़्यादातर फ़ीचर वैल्यू आम तौर पर, एक अलग रेंज में आती हैं. उदाहरण के लिए, कारों का वज़न आम तौर पर 907 से 2,268 किलोग्राम के बीच होता है और वे 3 से 21 किलोमीटर प्रति लीटर का माइलेज देती हैं. 8,000 पाउंड की कार या 100 मील प्रति गैलन का माइलेज देने वाली कार, सामान्य सीमा से बाहर है. इसलिए, इसे आउटलायर माना जाएगा.
आउटलायर का मतलब यह भी हो सकता है कि मॉडल की अनुमानित वैल्यू, असल वैल्यू से कितनी अलग हैं. उदाहरण के लिए, 3,000 पाउंड, कार के सामान्य वज़न की रेंज में आता है. वहीं, 40 मील प्रति गैलन, ईंधन की सामान्य खपत की रेंज में आता है. हालांकि, 3,000 पाउंड की कार, जो 40 मील प्रति गैलन का माइलेज देती है, वह मॉडल की भविष्यवाणी के हिसाब से एक आउटलायर होगी. ऐसा इसलिए, क्योंकि मॉडल का अनुमान होगा कि 3,000 पाउंड की कार, करीब 20 मील प्रति गैलन का माइलेज देगी.
सबसे सही लॉस फ़ंक्शन चुनते समय, इस बात का ध्यान रखें कि आपको मॉडल से आउटलायर को कैसे ट्रीट कराना है. उदाहरण के लिए, MSE मॉडल को आउटलायर की ओर ज़्यादा ले जाता है, जबकि MAE ऐसा नहीं करता. L2 लॉस, L1 लॉस की तुलना में आउटलायर के लिए ज़्यादा पेनल्टी लगाता है. उदाहरण के लिए, यहां दी गई इमेज में MAE का इस्तेमाल करके ट्रेन किए गए मॉडल और MSE का इस्तेमाल करके ट्रेन किए गए मॉडल को दिखाया गया है. लाल लाइन, पूरी तरह से ट्रेन किए गए मॉडल को दिखाती है. इसका इस्तेमाल अनुमान लगाने के लिए किया जाएगा. MAE का इस्तेमाल करके ट्रेन किए गए मॉडल की तुलना में, MSE का इस्तेमाल करके ट्रेन किए गए मॉडल के आउटलायर ज़्यादा करीब होते हैं.
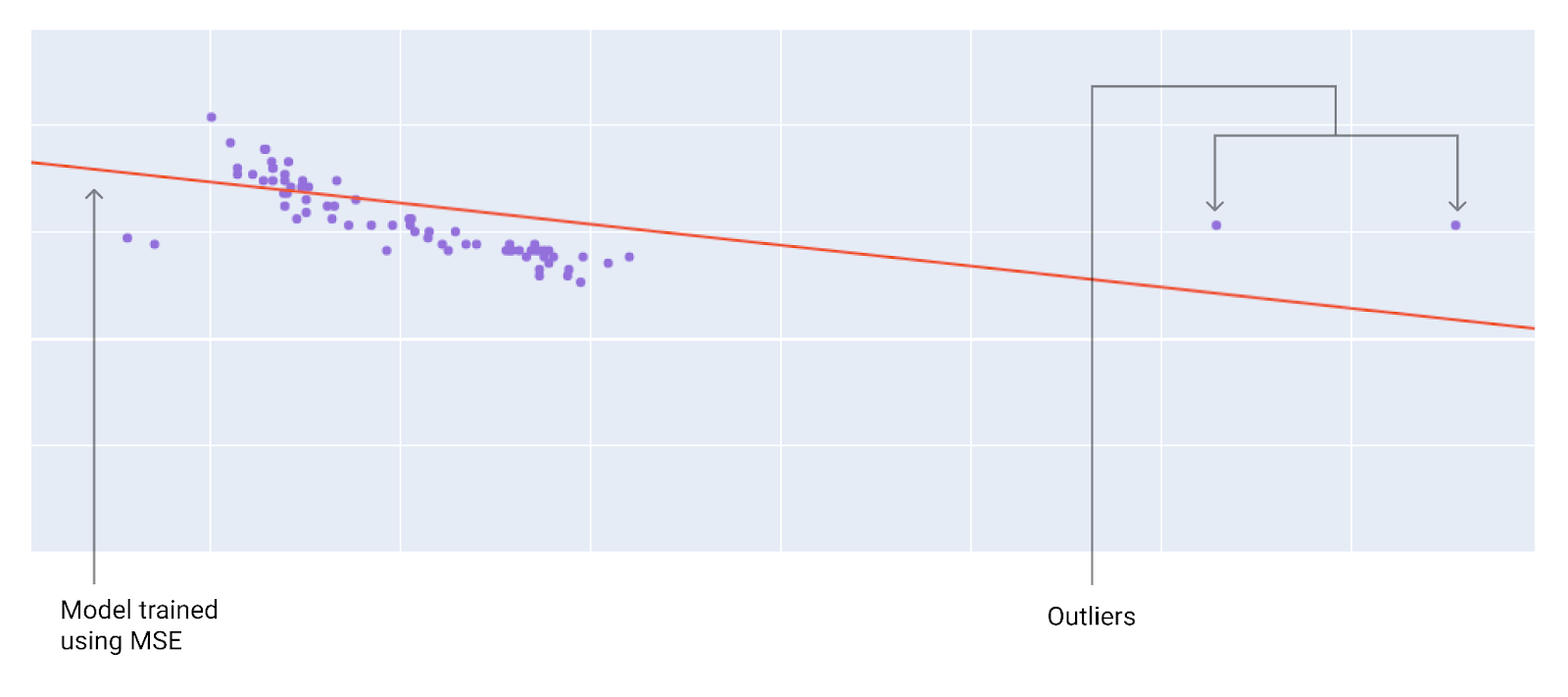
नौवीं इमेज. MSE लॉस, मॉडल को आउटलायर के ज़्यादा करीब ले जाता है.
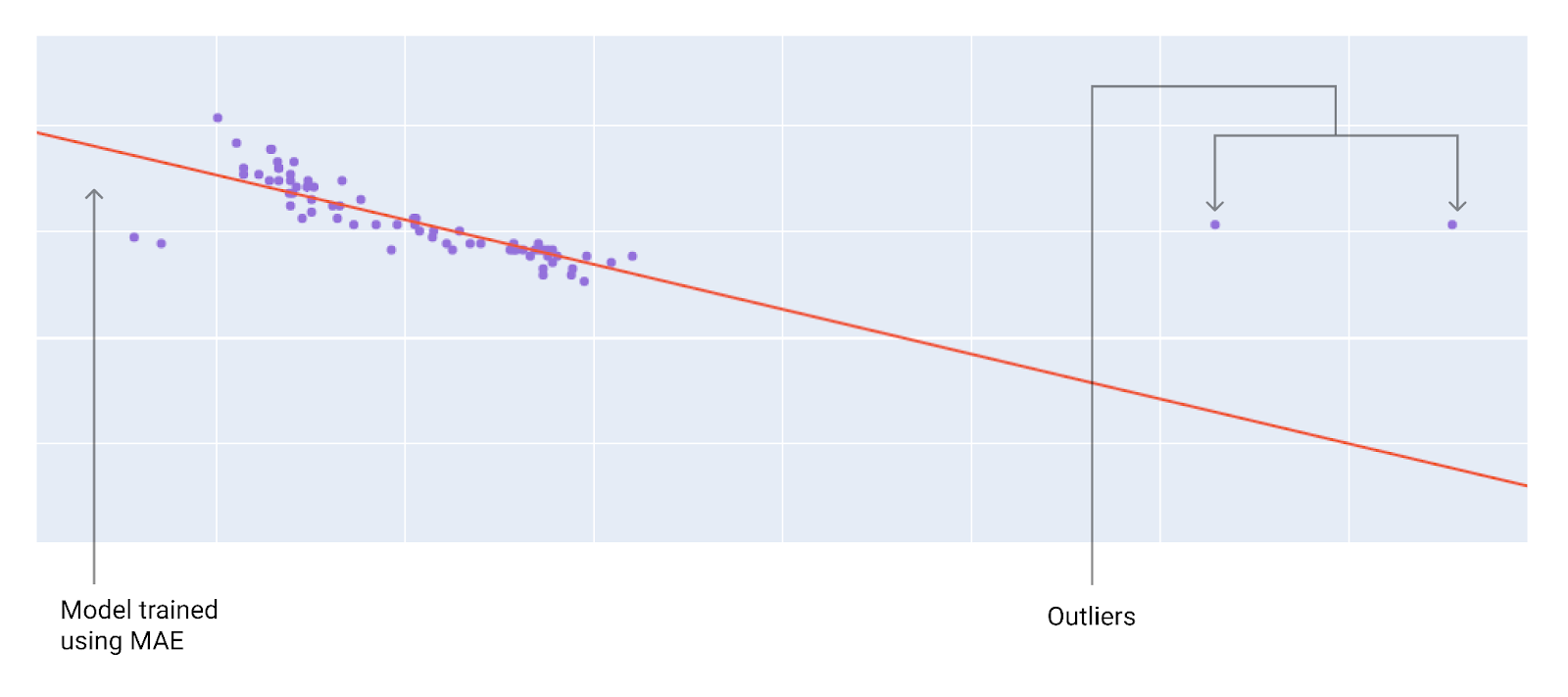
दसवीं इमेज. MAE लॉस, मॉडल को आउटलायर से दूर रखता है.
मॉडल और डेटा के बीच के संबंध पर ध्यान दें:
MSE. यह मॉडल, आउटलायर के ज़्यादा करीब है, लेकिन ज़्यादातर अन्य डेटा पॉइंट से दूर है.
MAE. मॉडल, आउटलायर से ज़्यादा दूर है, लेकिन ज़्यादातर अन्य डेटा पॉइंट के ज़्यादा करीब है.
देखें कि आपको कितना समझ आया
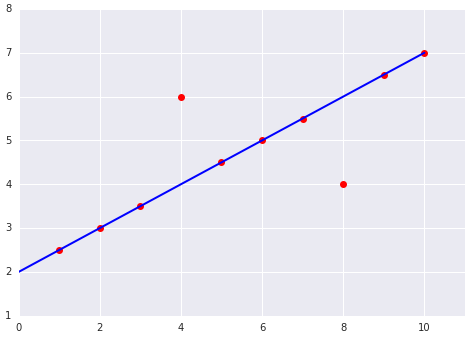
यहां दिए गए दो प्लॉट में, किसी डेटासेट के लिए फ़िट किए गए लीनियर मॉडल को दिखाया गया है:
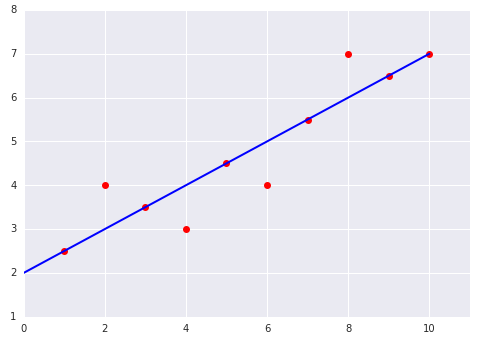
|
|
