Loss adalah metrik numerik yang menjelaskan seberapa salah prediksi model. Loss mengukur jarak antara prediksi model dan label sebenarnya. Tujuan melatih model adalah untuk meminimalkan kerugian, dengan menurunkannya ke nilai serendah mungkin.
Pada gambar berikut, Anda dapat memvisualisasikan kerugian sebagai panah yang ditarik dari titik data ke model. Panah menunjukkan seberapa jauh prediksi model dari nilai sebenarnya.
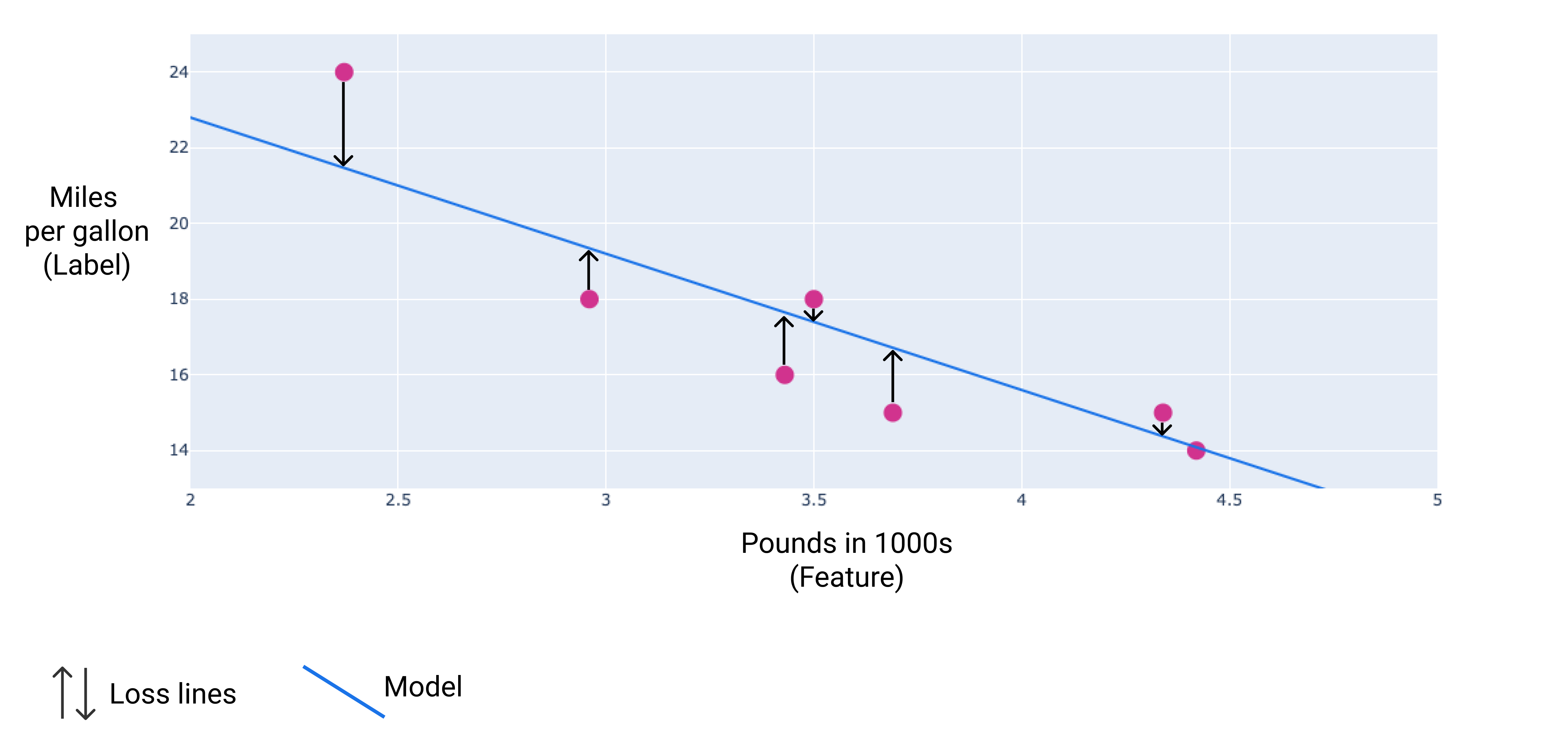
Gambar 8. Loss diukur dari nilai aktual ke nilai prediksi.
Jarak kehilangan
Dalam statistik dan machine learning, kerugian mengukur perbedaan antara nilai prediksi dan nilai aktual. Loss berfokus pada jarak antara nilai, bukan arah. Misalnya, jika model memprediksi 2, tetapi nilai sebenarnya adalah 5, kita tidak peduli bahwa kerugiannya negatif (2 – 5= –3). Sebaliknya, kita peduli bahwa jarak antara nilai adalah 3. Dengan demikian, semua metode untuk menghitung kerugian menghapus tanda.
Dua metode paling umum untuk menghapus tanda tersebut adalah sebagai berikut:
- Ambil nilai absolut dari perbedaan antara nilai aktual dan prediksi.
- Kuadratkan perbedaan antara nilai aktual dan prediksi.
Jenis kehilangan
Dalam regresi linear, ada lima jenis kerugian utama, yang diuraikan dalam tabel berikut.
| Jenis kehilangan | Definisi | Persamaan |
|---|---|---|
| L1 loss | Jumlah nilai absolut dari perbedaan antara nilai prediksi dan nilai aktual. | $ ∑ | nilai\ sebenarnya - nilai\ yang\ diprediksi | $ |
| Rata-rata error absolut (MAE) | Rata-rata kerugian L1 di seluruh set N contoh. | $ \frac{1}{N} ∑ | nilai\ sebenarnya - nilai\ prediksi | $ |
| L2 loss | Jumlah perbedaan kuadrat antara nilai prediksi dan nilai aktual. | $ ∑(nilai\ aktual - nilai\ prediksi)^2 $ |
| Rataan kuadrat galat (MSE) | Rata-rata kerugian L2 di seluruh set N contoh. | $ \frac{1}{N} ∑ (nilai\ sebenarnya - nilai\ prediksi)^2 $ |
| Error akar rataan kuadrat (RMSE) | Akar kuadrat dari rataan kuadrat galat (MSE). | $ \sqrt{\frac{1}{N} ∑ (nilai\ aktual - nilai\ prediksi)^2} $ |
Perbedaan fungsional antara kerugian L1 dan kerugian L2 (atau antara MAE/RMSE dan MSE) adalah penguadratan. Jika perbedaan antara prediksi dan label besar, penguadratan akan membuat kerugian menjadi lebih besar. Jika perbedaannya kecil (kurang dari 1), penguadratan akan membuat kerugian menjadi lebih kecil.
Metrik kerugian seperti MAE dan RMSE mungkin lebih disukai daripada kerugian L2 atau MSE dalam beberapa kasus penggunaan karena cenderung lebih mudah ditafsirkan oleh manusia, karena mengukur error menggunakan skala yang sama dengan nilai prediksi model.
Saat memproses beberapa contoh sekaligus, sebaiknya hitung rata-rata kerugian di semua contoh, baik menggunakan MAE, MSE, atau RMSE.
Contoh penghitungan kerugian
Di bagian sebelumnya, kita membuat model berikut untuk memprediksi efisiensi bahan bakar berdasarkan berat mobil:
- Model: $ y' = 34 + (-4.6)(x_1) $
- Berat: $ –4,6 $
- Bias: $ 34 $
Jika model memprediksi bahwa mobil seberat 2.370 pound mendapatkan 23,1 mil per galon, tetapi sebenarnya mendapatkan 24 mil per galon, kita akan menghitung kerugian L2 sebagai berikut:
| Nilai | Persamaan | Hasil |
|---|---|---|
| Prediksi | $\small{bias + (bobot * nilai\ fitur)}$ $\small{34 + (-4.6*2.37)}$ |
$\small{23.1}$ |
| Nilai sebenarnya | $ \small{ label } $ | $ \small{ 24 } $ |
| Kerugian L2 | $ \small{ (nilai\ sebenarnya - nilai\ prediksi)^2 } $ $\small{ (24 - 23,1)^2 }$ |
$\small{0.81}$ |
Dalam contoh ini, kerugian L2 untuk satu titik data tersebut adalah 0,81.
Memilih kerugian
Keputusan untuk menggunakan MAE atau MSE dapat bergantung pada set data dan cara Anda ingin menangani prediksi tertentu. Sebagian besar nilai fitur dalam set data biasanya berada dalam rentang yang berbeda. Misalnya, mobil biasanya memiliki berat antara 2.000 dan 5.000 pon serta mendapatkan 8 hingga 50 mil per galon. Mobil seberat 3.600 kg, atau mobil yang menempuh 100 mil per galon, berada di luar rentang umum dan akan dianggap sebagai pencilan.
Pencilan juga dapat merujuk pada seberapa jauh prediksi model dari nilai sebenarnya. Misalnya, 3.000 pon berada dalam rentang berat mobil standar, dan 40 mil per galon berada dalam rentang efisiensi bahan bakar standar. Namun, mobil seberat 3.000 pound yang memiliki efisiensi bahan bakar 40 mil per galon akan menjadi pencilan dalam hal prediksi model karena model akan memprediksi bahwa mobil seberat 3.000 pound akan memiliki efisiensi bahan bakar sekitar 20 mil per galon.
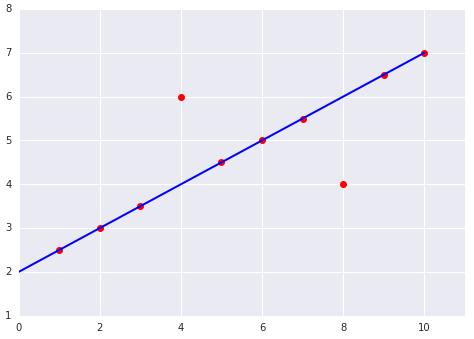
Saat memilih fungsi kerugian terbaik, pertimbangkan cara yang Anda inginkan agar model memperlakukan pencilan. Misalnya, MSE menggerakkan model lebih ke arah pencilan, sedangkan MAE tidak. Kerugian L2 menimbulkan penalti yang jauh lebih tinggi untuk pencilan daripada kerugian L1. Misalnya, gambar berikut menunjukkan model yang dilatih menggunakan MAE dan model yang dilatih menggunakan MSE. Garis merah mewakili model terlatih sepenuhnya yang akan digunakan untuk membuat prediksi. Pencilan lebih dekat dengan model yang dilatih dengan MSE daripada model yang dilatih dengan MAE.
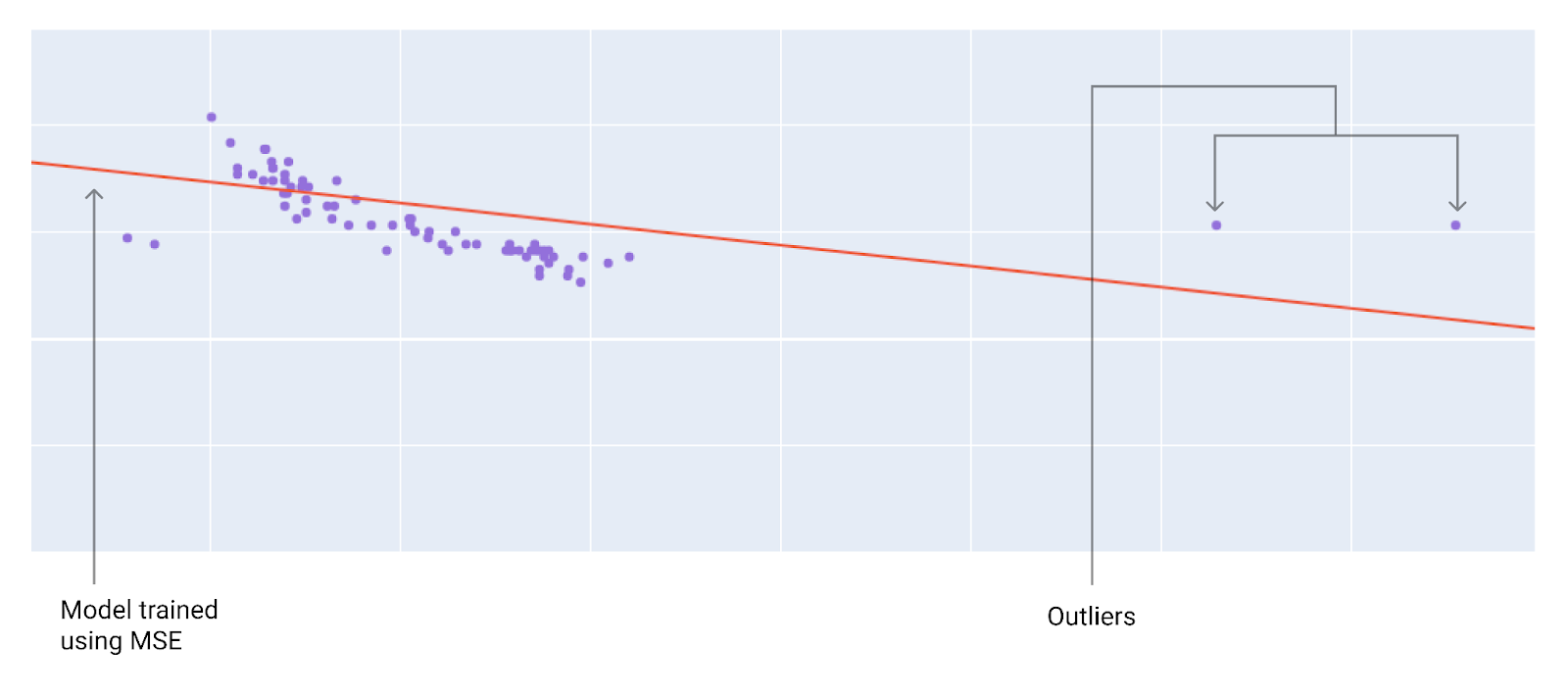
Gambar 9. Kerugian MSE membuat model lebih dekat dengan pencilan.
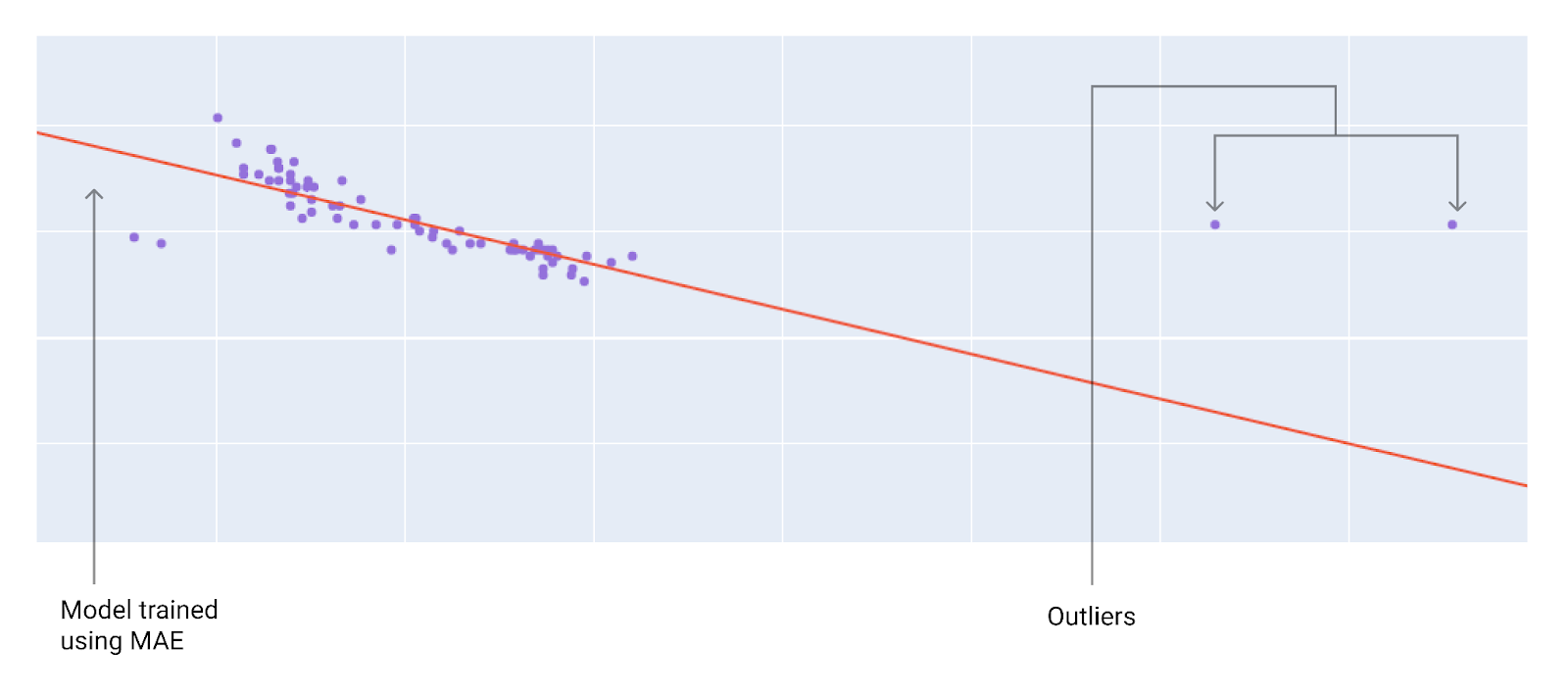
Gambar 10. Kerugian MAE membuat model lebih jauh dari pencilan.
Perhatikan hubungan antara model dan data:
MSE. Model lebih dekat dengan pencilan, tetapi lebih jauh dari sebagian besar titik data lainnya.
MAE. Model ini lebih jauh dari pencilan, tetapi lebih dekat dengan sebagian besar titik data lainnya.
Periksa Pemahaman Anda
Pertimbangkan dua plot berikut dari kecocokan model linear dengan set data:
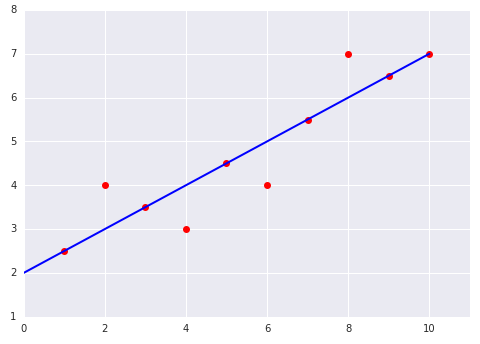
|
|
