A perda é uma métrica numérica que descreve o quão erradas são as previsões de um modelo. A perda mede a distância entre as previsões do modelo e os rótulos reais. O objetivo de treinar um modelo é minimizar a perda, reduzindo-a ao menor valor possível.
Na imagem a seguir, é possível visualizar a perda como setas desenhadas dos pontos de dados para o modelo. As setas mostram a distância entre as previsões do modelo e os valores reais.
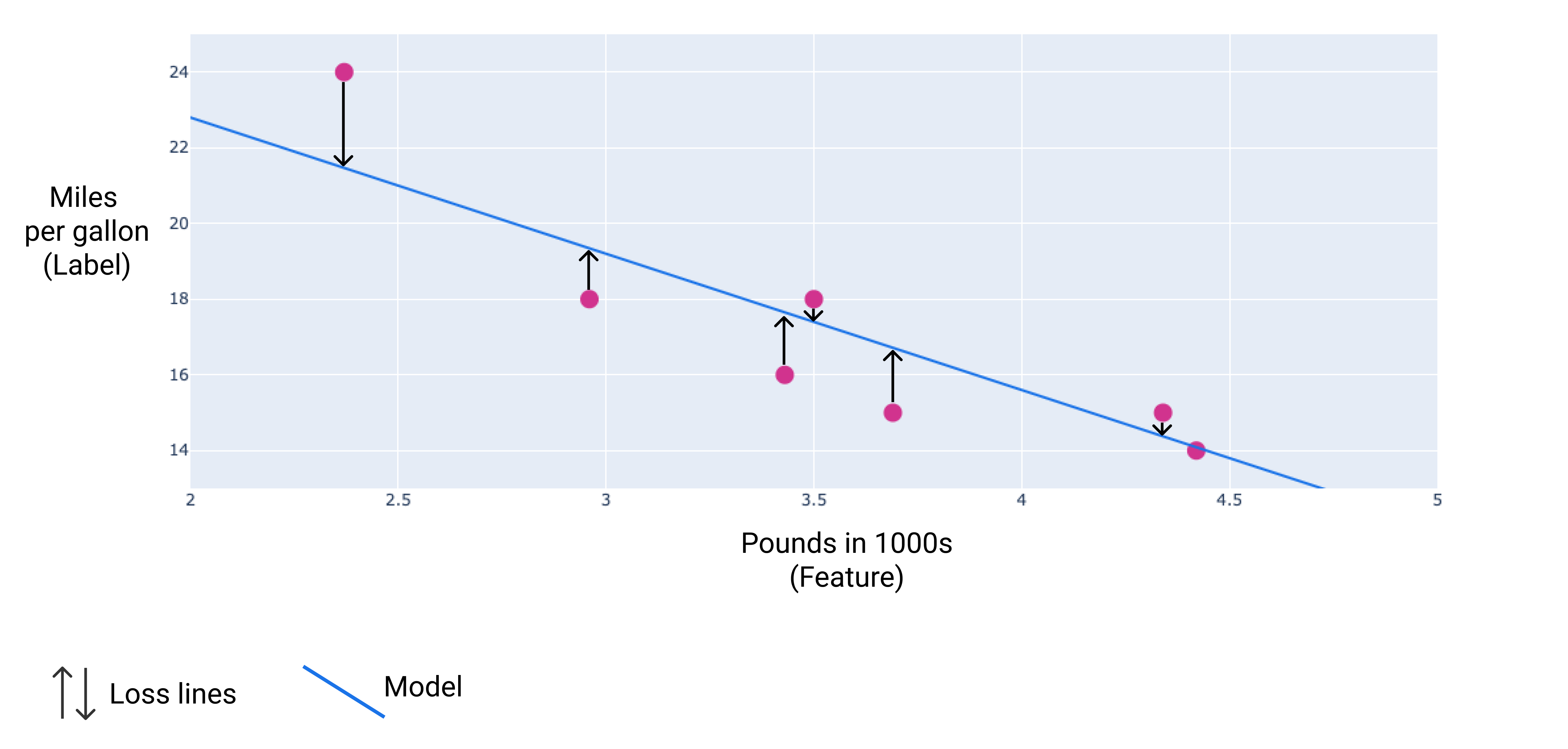
Figura 8. A perda é medida do valor real para o valor previsto.
Distância da perda
Em estatística e machine learning, a perda mede a diferença entre os valores previstos e reais. A perda se concentra na distância entre os valores, não na direção. Por exemplo, se um modelo prevê 2, mas o valor real é 5, não importa que a perda seja negativa ($ 2-5=-3 $). Em vez disso, importa que a distância entre os valores seja $ 3 $. Portanto, todos os métodos para calcular a perda removem o sinal.
Confira abaixo os dois métodos mais comuns para remover o sinal:
- Calcule o valor absoluto da diferença entre o valor real e a previsão.
- Eleve ao quadrado a diferença entre o valor real e a previsão.
Tipos de perda
Na regressão linear, há cinco tipos principais de perda, que são descritos na tabela a seguir.
| Tipo de perda | Definição | Equação |
|---|---|---|
| Perda L1 | A soma dos valores absolutos da diferença entre os valores previstos e os reais. | $ ∑ | actual\ value - predicted\ value | $ |
| Erro médio absoluto (MAE) | A média das perdas L1 em um conjunto de N exemplos. | $ \frac{1}{N} ∑ | actual\ value - predicted\ value | $ |
| Perda L2 | A soma da diferença quadrática entre os valores previstos e os valores reais. | $ ∑(valor\ real - valor\ previsto)^2 $ |
| Erro quadrático médio (EQM) | A média das perdas L2 em um conjunto de N exemplos. | $ \frac{1}{N} ∑ (actual\ value - predicted\ value)^2 $ |
| Raiz do erro quadrático médio (RMSE) | A raiz quadrada do erro quadrático médio (EQM). | $ \sqrt{\frac{1}{N} ∑ (actual\ value - predicted\ value)^2} $ |
A diferença funcional entre a perda L1 e a perda L2 (ou entre MAE/RMSE e MSE) é a elevação ao quadrado. Quando a diferença entre a previsão e o rótulo é grande, a elevação ao quadrado aumenta ainda mais a perda. Quando a diferença é pequena (menos de 1), a elevação ao quadrado torna a perda ainda menor.
Métricas de perda como MAE e RMSE podem ser preferíveis à perda L2 ou MSE em alguns casos de uso porque tendem a ser mais interpretáveis por humanos, já que medem o erro usando a mesma escala do valor previsto do modelo.
Ao processar vários exemplos de uma só vez, recomendamos calcular a média das perdas em todos os exemplos, seja usando MAE, MSE ou RMSE.
Exemplo de cálculo de perda
Usando a linha de melhor ajuste anterior, vamos calcular a perda L2 para um único exemplo. Da linha de melhor ajuste, tivemos os seguintes valores para peso e viés:
- $ \small{Peso: -4.6} $
- $ \small{Bias: 34} $
Se o modelo prevê que um carro de 1.075 kg faz 9,8 km por litro, mas na verdade faz 11 km por litro, calculamos a perda L2 da seguinte forma:
| Valor | Equação | Resultado |
|---|---|---|
| Previsão | $\small{bias + (weight * feature\ value)}$ $\small{34 + (-4.6*2.37)}$ |
$\small{23.1}$ |
| Valor real | $ \small{ label } $ | $ \small{ 26 } $ |
| Perda L2 | $ \small{ (actual\ value - predicted\ value)^2 } $ $\small{ (26 - 23.1)^2 }$ |
$\small{8.41}$ |
Neste exemplo, a perda L2 para esse único ponto de dados é 8,41.
Como escolher uma perda
A decisão de usar MAE ou MSE depende do conjunto de dados e da maneira como você quer lidar com determinadas previsões. A maioria dos valores de recursos em um conjunto de dados geralmente fica dentro de um intervalo distinto. Por exemplo, os carros normalmente pesam entre 900 e 2.200 quilos e fazem entre 3 e 21 quilômetros por litro. Um carro de 3.600 kg ou que faz 160 km por galão está fora do intervalo típico e seria considerado um outlier.
Um outlier também pode se referir à distância entre as previsões de um modelo e os valores reais. Por exemplo, 1.360 quilos está dentro da faixa de peso típica de um carro, e 64 quilômetros por galão está dentro da faixa de eficiência de combustível típica. No entanto, um carro de 1.360 kg que faz 64 km por galão seria um outlier em termos de previsão do modelo, porque ele prevê que um carro de 1.360 kg faria cerca de 32 km por galão.
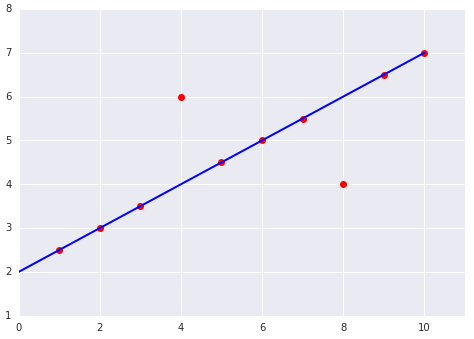
Ao escolher a melhor função de perda, considere como você quer que o modelo trate os outliers. Por exemplo, o MSE move o modelo mais para os outliers, enquanto o MAE não. A perda L2 gera uma penalidade muito maior para um outlier do que a perda L1. Por exemplo, as imagens a seguir mostram um modelo treinado usando MAE e outro treinado usando MSE. A linha vermelha representa um modelo totalmente treinado que será usado para fazer previsões. Os outliers estão mais próximos do modelo treinado com MSE do que do modelo treinado com MAE.
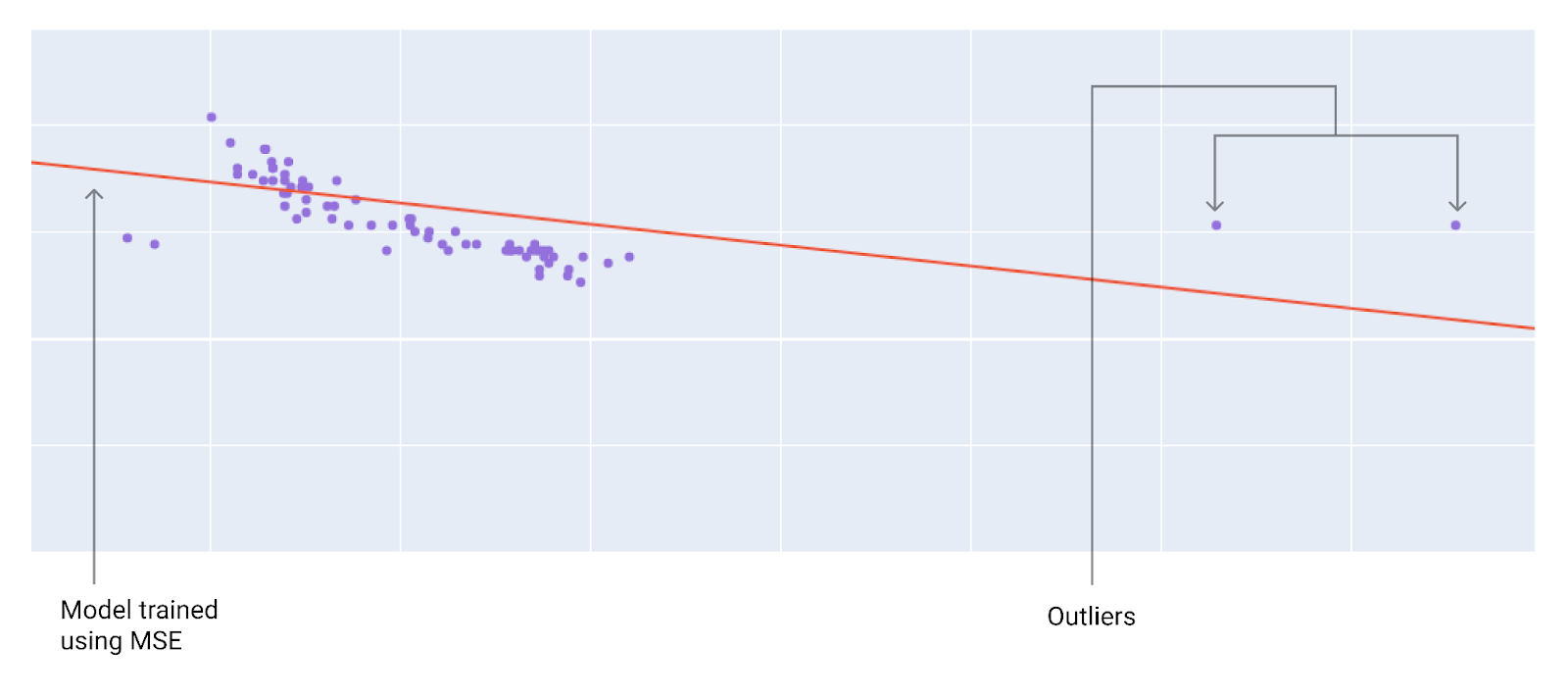
Figura 9. A perda de EQM aproxima o modelo dos outliers.
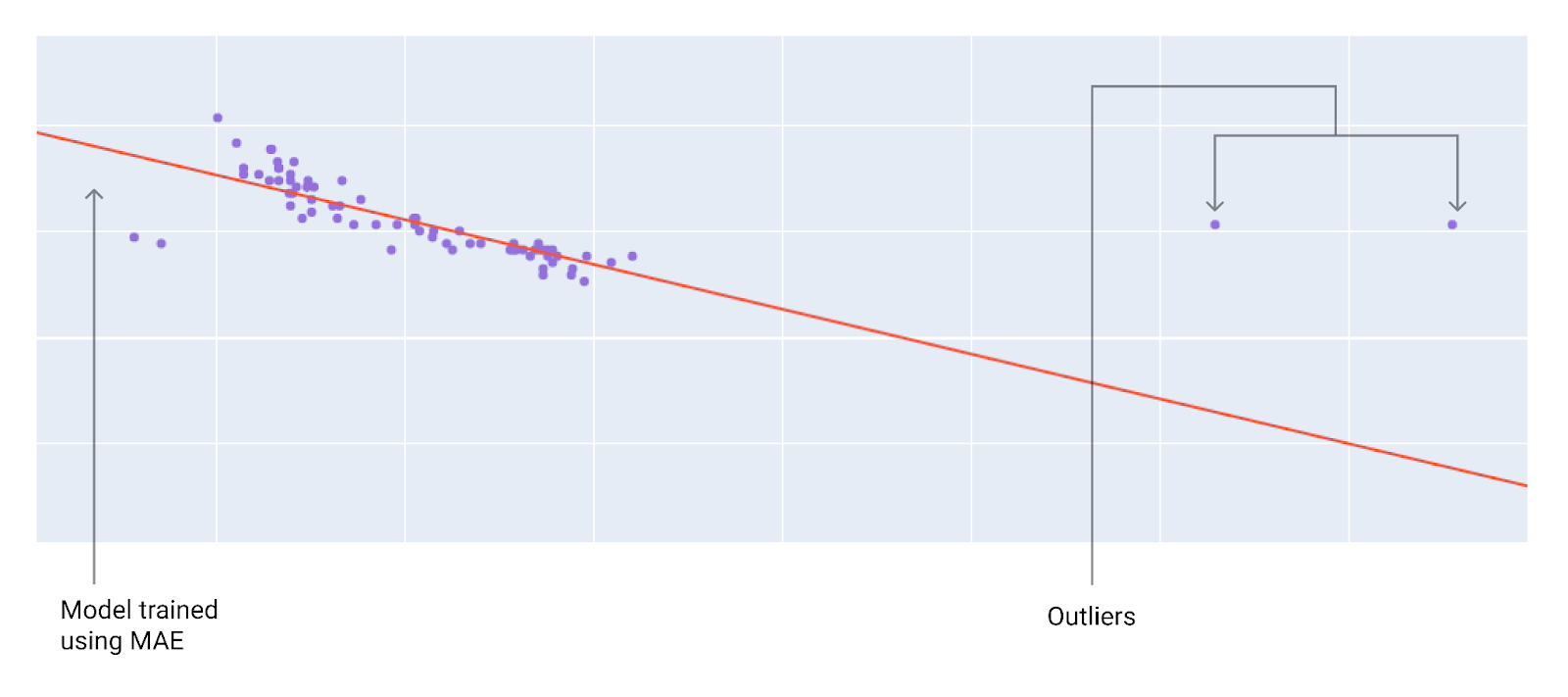
Figura 10. A perda de MAE mantém o modelo mais distante dos outliers.
Observe a relação entre o modelo e os dados:
MSE. O modelo está mais próximo dos outliers, mas mais distante da maioria dos outros pontos de dados.
MAE. O modelo fica mais distante dos outliers, mas mais perto da maioria dos outros pontos de dados.
Teste seu conhecimento
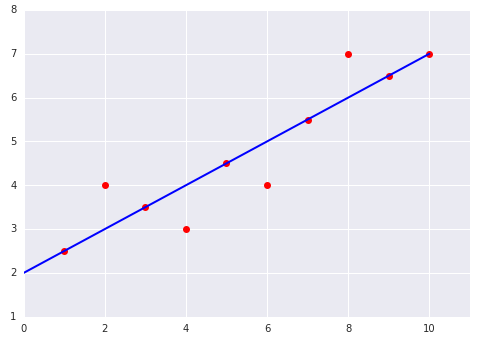
Considere estes dois gráficos de um modelo linear ajustado a um conjunto de dados:
|
|
