רגרסיה לינארית: תרגיל בנושא פרמטרים
קל לארגן דפים בעזרת אוספים
אפשר לשמור ולסווג תוכן על סמך ההעדפות שלך.
בתרשים שלמטה מוצגים 20 דוגמאות מתוך מערך נתונים של צריכת דלק. התכונה (משקל הרכב באלפי פאונד) מוצגת בציר ה-X והתווית (מיילים לגלון) מוצגת בציר ה-Y.
המשימה שלכם: להזיז את הסליידרים Weight ו-Bias שמעל הגרף כדי למצוא את המודל הלינארי שממזער את הפסד ה-MSE בנתונים.
שאלות שכדאי לחשוב עליהן:
- מהו ה-MSE הכי נמוך שאפשר להשיג?
- אילו ערכים של משקל והטיה הניבו את ההפסד הזה?
לוחצים על סמל הפלוס כדי לראות את הפתרון.
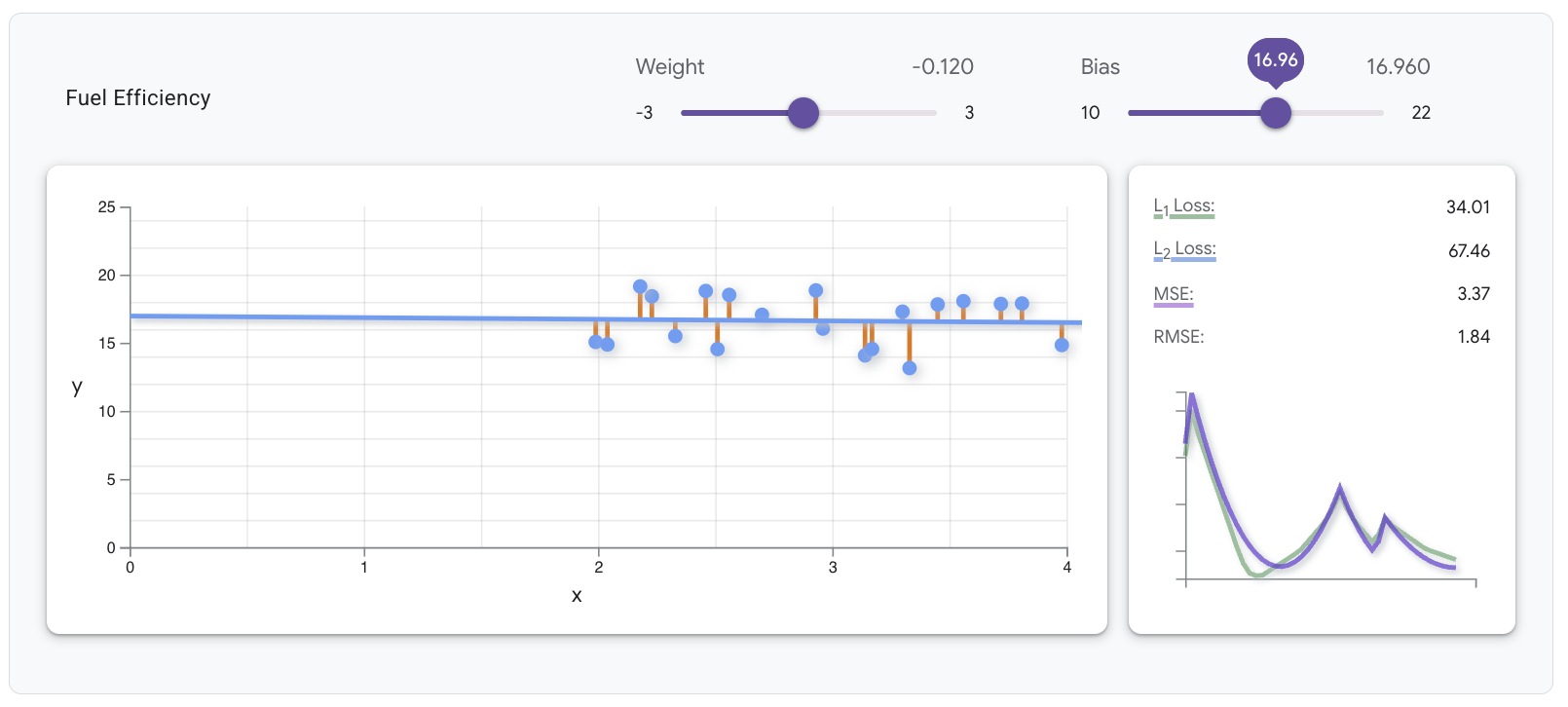
למודל הלינארי האופטימלי לנתונים האלה יש MSE של 3.37, עם משקל של –0.12 והטיה של 16.96, כמו שמוצג בתמונה הבאה.
אלא אם צוין אחרת, התוכן של דף זה הוא ברישיון Creative Commons Attribution 4.0 ודוגמאות הקוד הן ברישיון Apache 2.0. לפרטים, ניתן לעיין במדיניות האתר Google Developers. Java הוא סימן מסחרי רשום של חברת Oracle ו/או של השותפים העצמאיים שלה.
עדכון אחרון: 2025-07-09 (שעון UTC).
[null,null,["עדכון אחרון: 2025-07-09 (שעון UTC)."],[],[],null,["# Linear regression: Parameters exercise\n\nThe graph below plots 20 examples from a fuel-efficiency dataset, with the\nfeature (car heaviness in thousands of pounds) plotted on the x-axis and the\nlabel (miles per gallon) plotted on the y-axis.\n\n**Your task:** Adjust the **Weight** and **Bias** sliders above the graph to\nfind the linear model that minimizes MSE loss on the data.\n\n**Questions to consider:**\n\n- What is the lowest MSE you can achieve?\n- What weight and bias values produced this loss?\n\n#### Click the plus icon to see the solution\n\nThe optimal linear model for this data has an MSE of 3.37, with a\nweight of --0.12 and a bias of 16.96, as shown in the following image."]]
