In diesem Modul werden Konzepte der linearen Regression vorgestellt.
Lineare Regression ist eine statistischen Verfahren, mit dem die Beziehung zwischen Variablen ermittelt wird. In einem ML-System Kontext zu verstehen, findet die lineare Regression die Beziehung zwischen features und ein label
Angenommen, wir möchten den Kraftstoffverbrauch eines Autos in Meilen pro Gallone basierend auf dem Gewicht des Autos, und wir haben folgendes Dataset:
| Pfund in 1.000 s (Feature) | Meilen pro Gallone (Label) |
|---|---|
| 3,5 | 18 |
| 3,69 | 15 |
| 3,44 | 18 |
| 3,43 | 16 |
| 4,34 | 15 |
| 4,42 | 14 |
| 2,37 | 24 |
Wenn wir diese Punkte grafisch darstellen, erhalten wir die folgende Grafik:
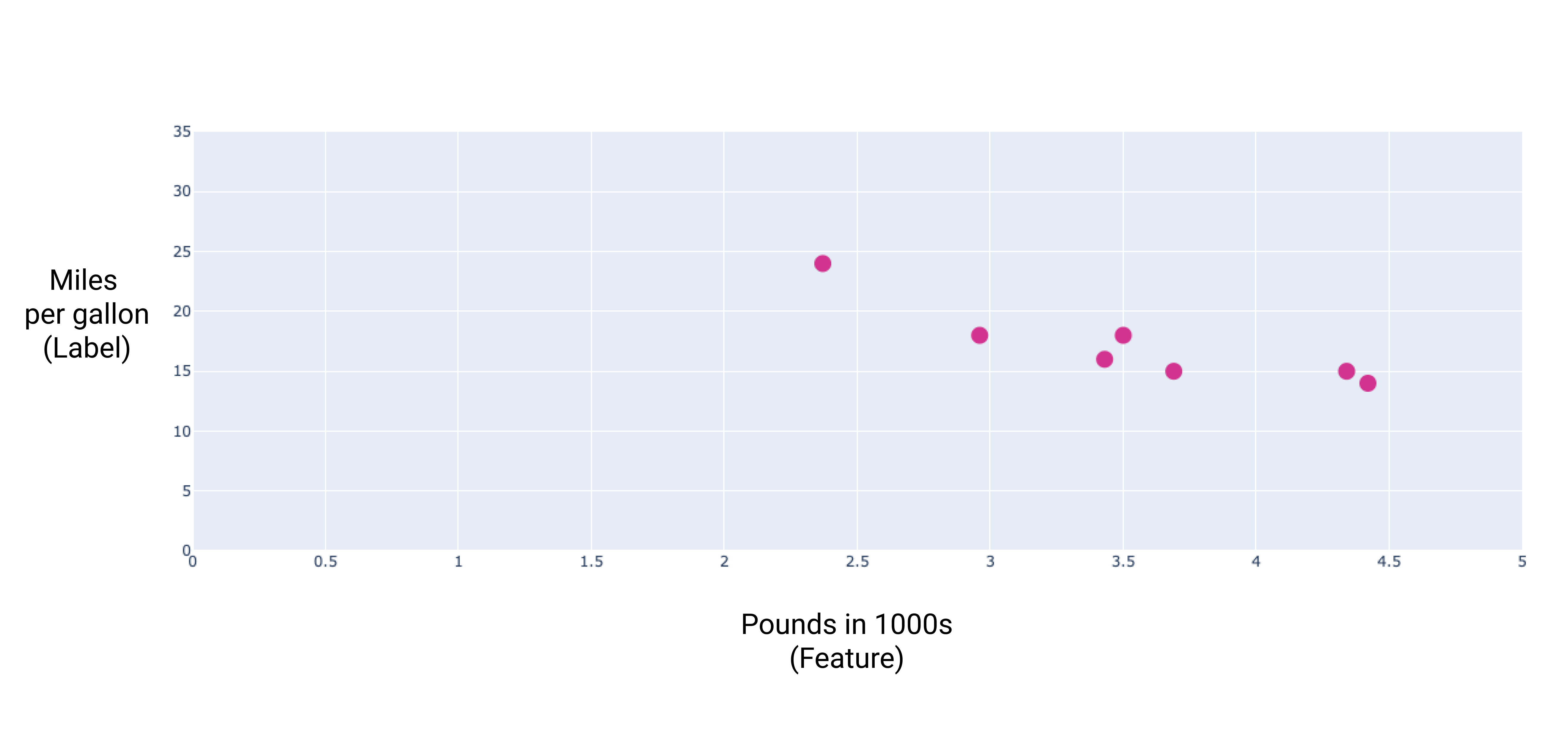
Abbildung 1. Schweregrad des Autos (in Pfund) im Vergleich zu Meilen pro Gallone. Als schwerer und weniger Kilometer pro Gallone.
Wir könnten unser eigenes Modell erstellen, indem wir eine am besten passende Linie durch die Punkte zeichnen:
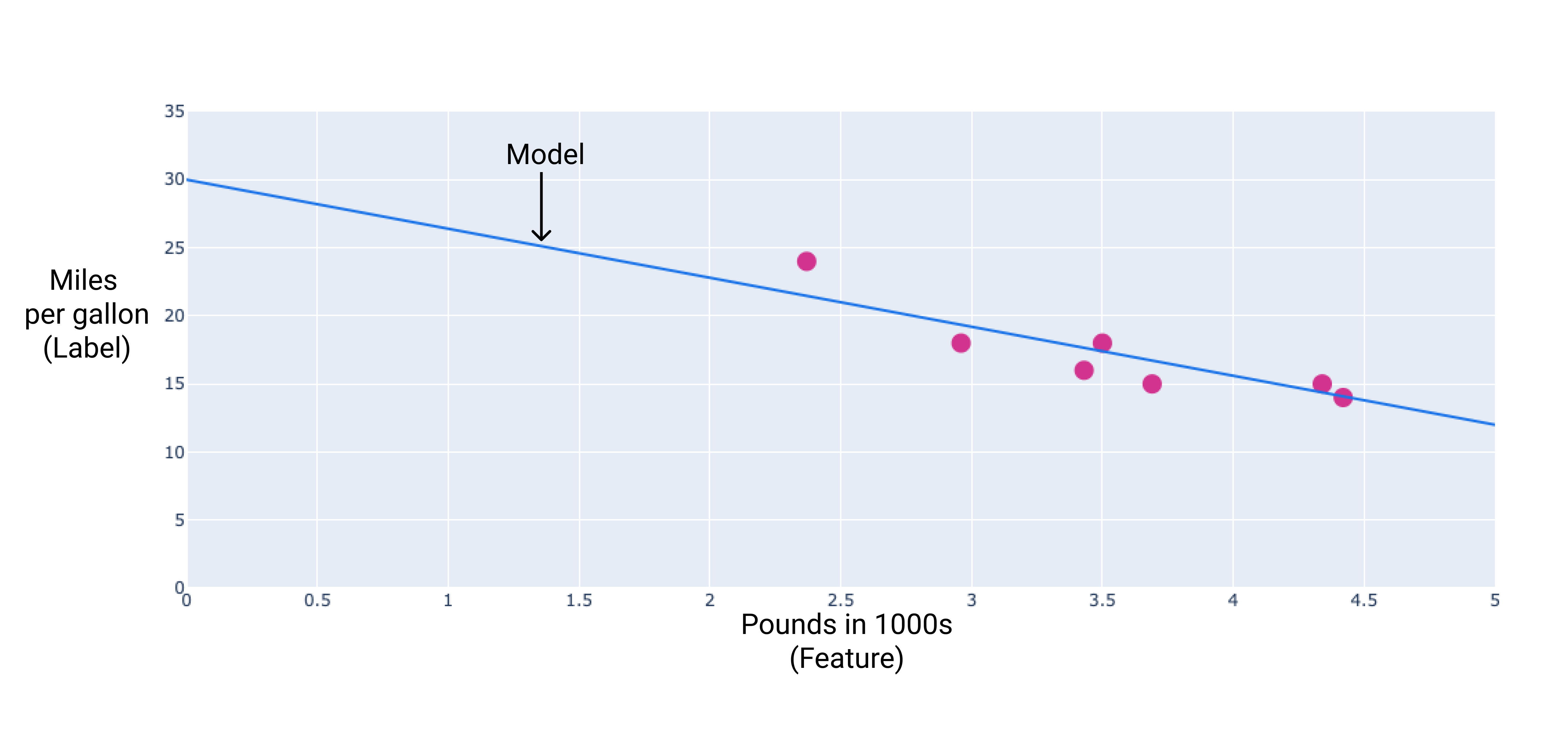
Abbildung 2. Eine am besten passende Linie, die durch die Daten aus der vorherigen Abbildung gezeichnet wird.
Lineare Regressionsgleichung
In der algebraischen Perspektive wäre das Modell wie folgt definiert: $ y = mx + b $, wobei
- $ y $ steht für Meilen pro Gallone – der Wert, den wir vorhersagen möchten.
- $ m $ ist die Steigung der Linie.
- $ x $ sind Pfund – unser Eingabewert.
- $ b $ ist der y-Achsenabschnitt.
In ML schreiben wir die Gleichung für ein lineares Regressionsmodell so:
Dabei gilt:
- $ y' $ ist das vorhergesagte Label – die Ausgabe.
- $ b $ ist die Voreingenommenheit. des Modells. Das Konzept der Verzerrung entspricht dem Konzept des y-Achsenabschnitts in der algebraischen Gleichung für eine Linie. In ML wird die Verzerrung manchmal als $ w_0 $ bezeichnet. Verzerrung ist ein Parameter des Modells und während des Trainings berechnet.
- $ w_1 $ ist die Gewichtung von . Das Gewichtung ist dasselbe Konzept wie die Steigung $ m $ in der algebraischen Gleichung für eine Linie. Das Gewicht entspricht parameter des Modells und ist die während des Trainings berechnet werden.
- $ x_1 $ ist eine Funktion, das heißt, Eingabe.
Während des Trainings berechnet das Modell die Gewichtung und Verzerrung, die das beste Ergebnis liefern. Modell.
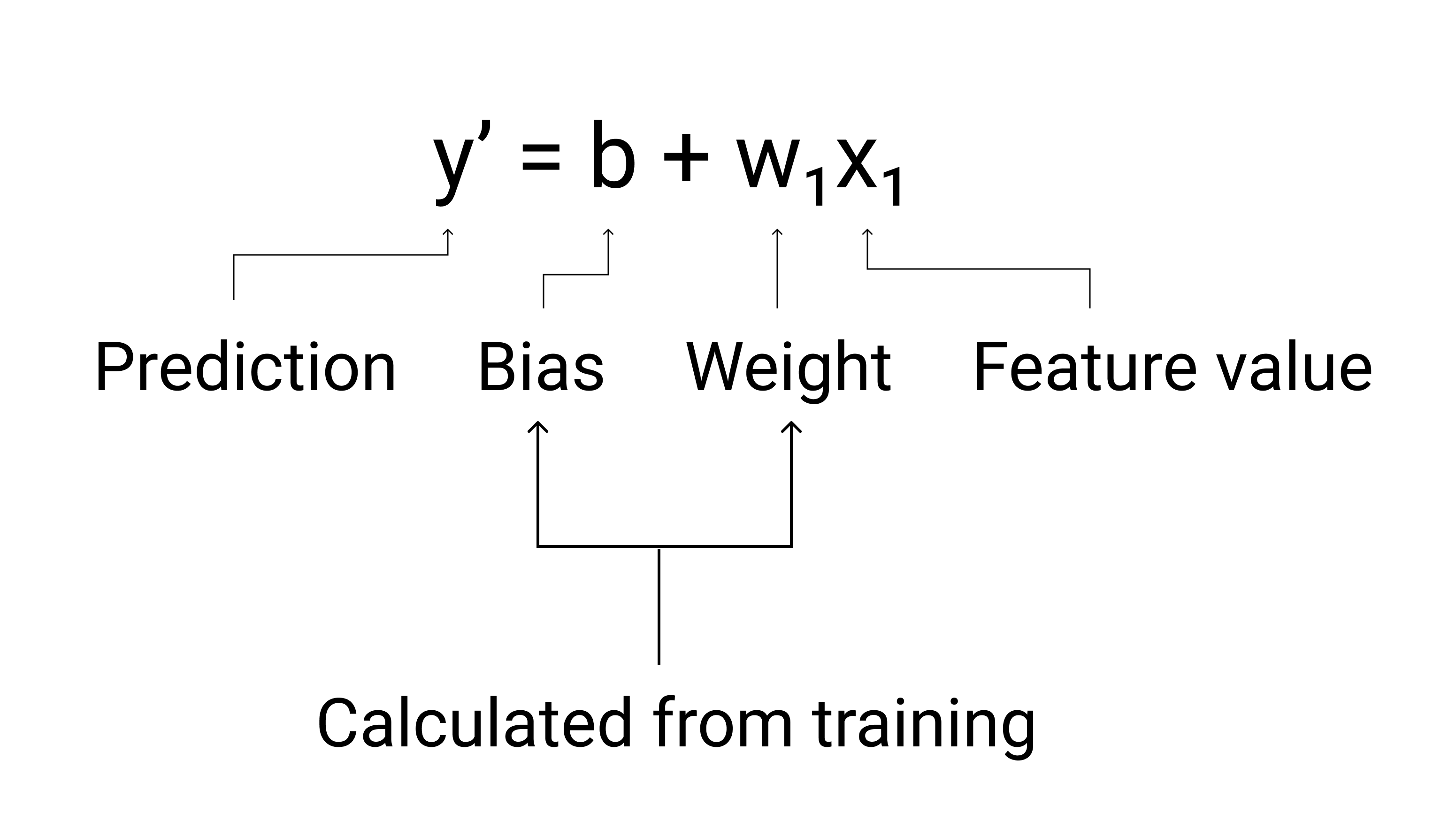
Abbildung 3. Mathematische Darstellung eines linearen Modells.
In unserem Beispiel berechnen wir die Gewichtung und Verzerrung anhand der von uns gezeichneten Linie. Die Bias beträgt 30 (wobei die Linie die Y-Achse schneidet), und die Gewichtung beträgt -3,6 (die Steigung der Linie). Das Modell wäre definiert als $ y' = 30 + (-3.6)(x_1) $ und könnten wir damit Vorhersagen treffen. Bei diesem Modell wird z. B. ein Das Auto mit einem Gewicht von 1.200 kg hat eine vorhergesagte Kraftstoffeffizienz von 25,2 Kilometern pro Gallone.
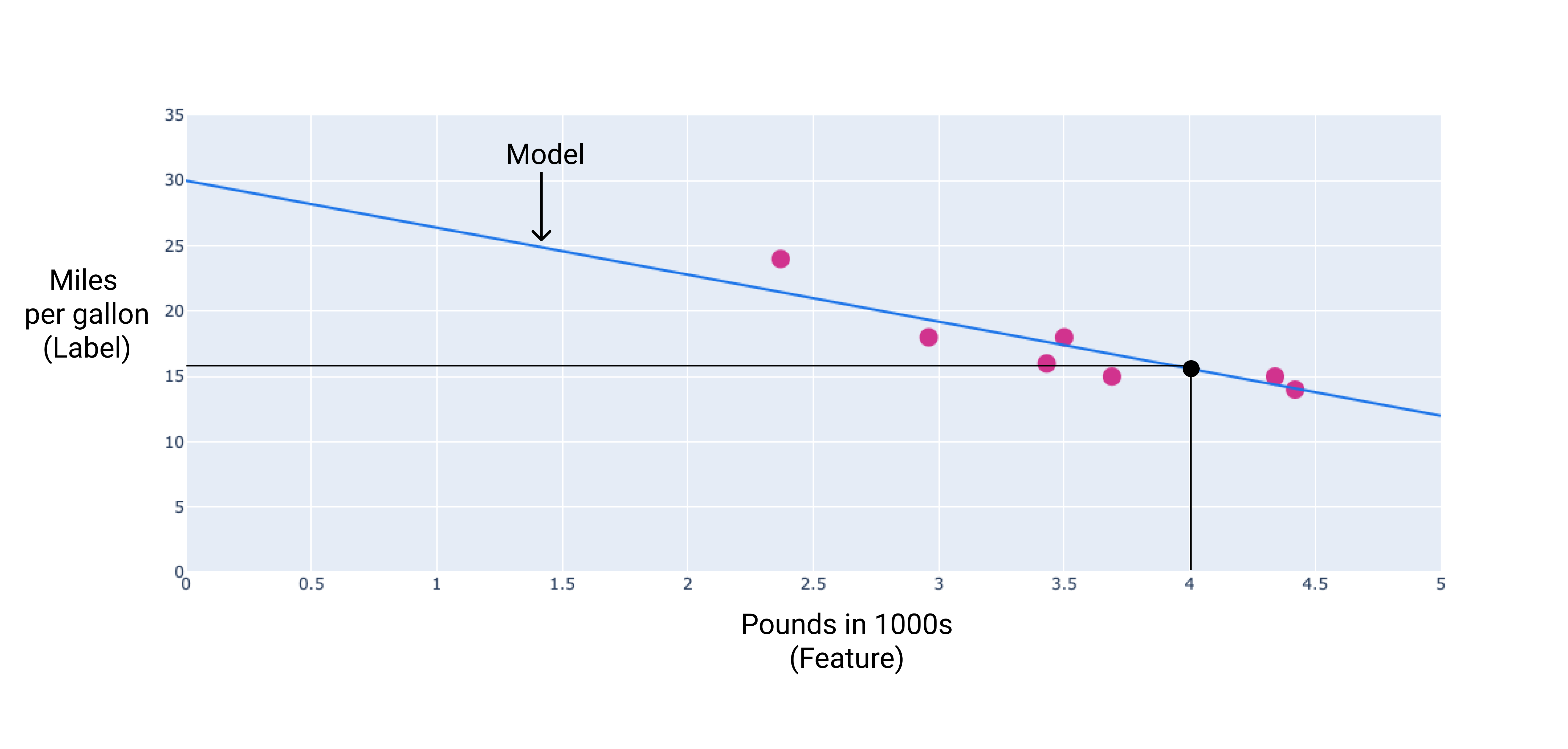
Abbildung 4. Mithilfe dieses Modells hat ein ca. 1.800 kg schweres Auto eine vorhergesagte von 25,1 Kilometern pro Gallone.
Modelle mit mehreren Features
Obwohl im Beispiel in diesem Abschnitt nur eine Funktion verwendet wird – die Schwere des Fahrzeugs – ein komplexeres Modell basiert möglicherweise auf mehreren Funktionen, die jeweils eine separate Gewichtung haben ($ w_1 $, $ w_2 $ usw.). Beispiel: Ein Modell der auf fünf Funktionen beruht, würden wie folgt geschrieben:
$ y' = b + w_1x_1 + w_2x_2 + w_3x_3 + w_4x_4 + w_5x_5 $
Zum Beispiel könnte ein Modell, das den Kraftstoffverbrauch vorhersagt, zusätzlich Features wie zum Beispiel:
- Motorhub
- Beschleunigung
- Zylinderanzahl
- Pferdestärke
Dieses Modell würde so geschrieben werden:
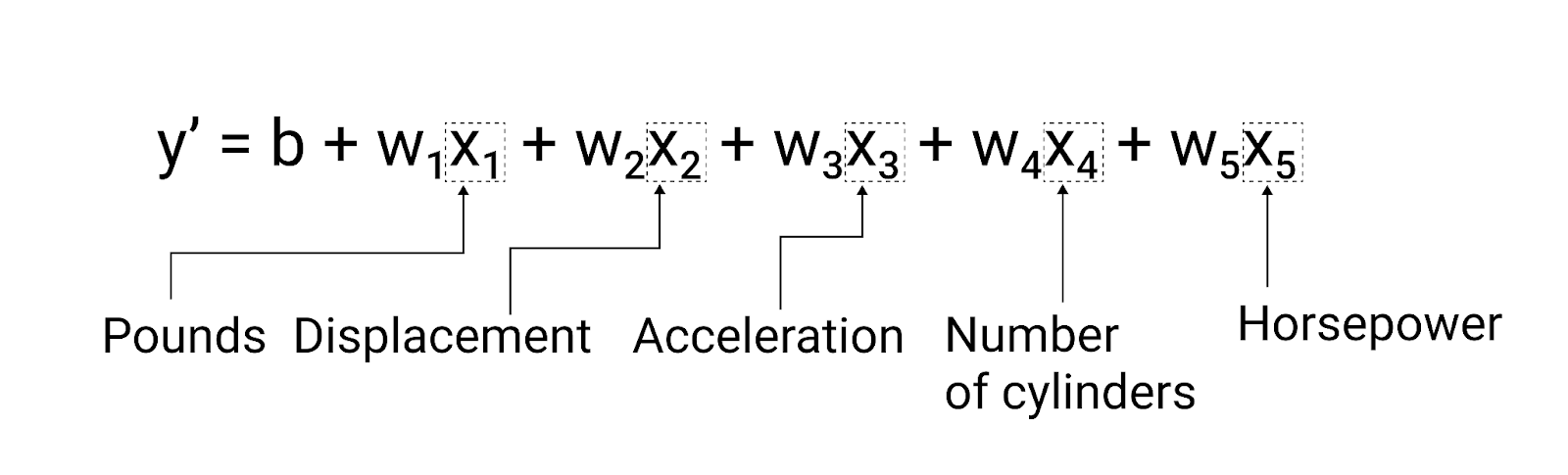
Abbildung 5. Ein Modell mit fünf Merkmalen, um die Kilometer pro Gallone vorherzusagen Bewertung.
Die grafische Darstellung einiger dieser zusätzlichen Funktionen zeigt, lineare Beziehung zum Label, Meilen pro Gallone:
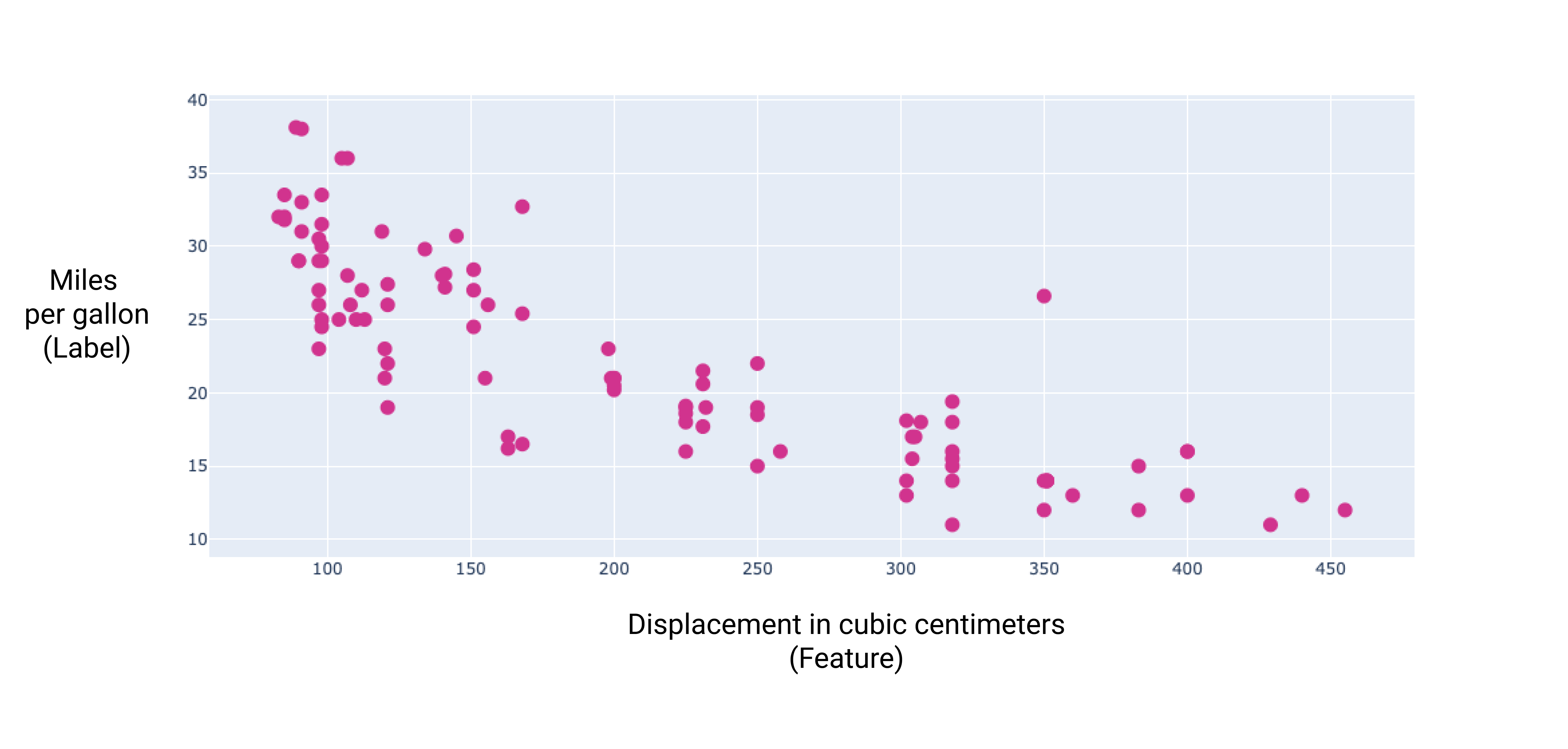
Abbildung 6. Der Verdrängung eines Autos in Kubikzentimetern und die Kilometer pro Gallone Bewertung. Je größer der Motor wird, desto mehr Kilometer pro Liter nimmt ab.
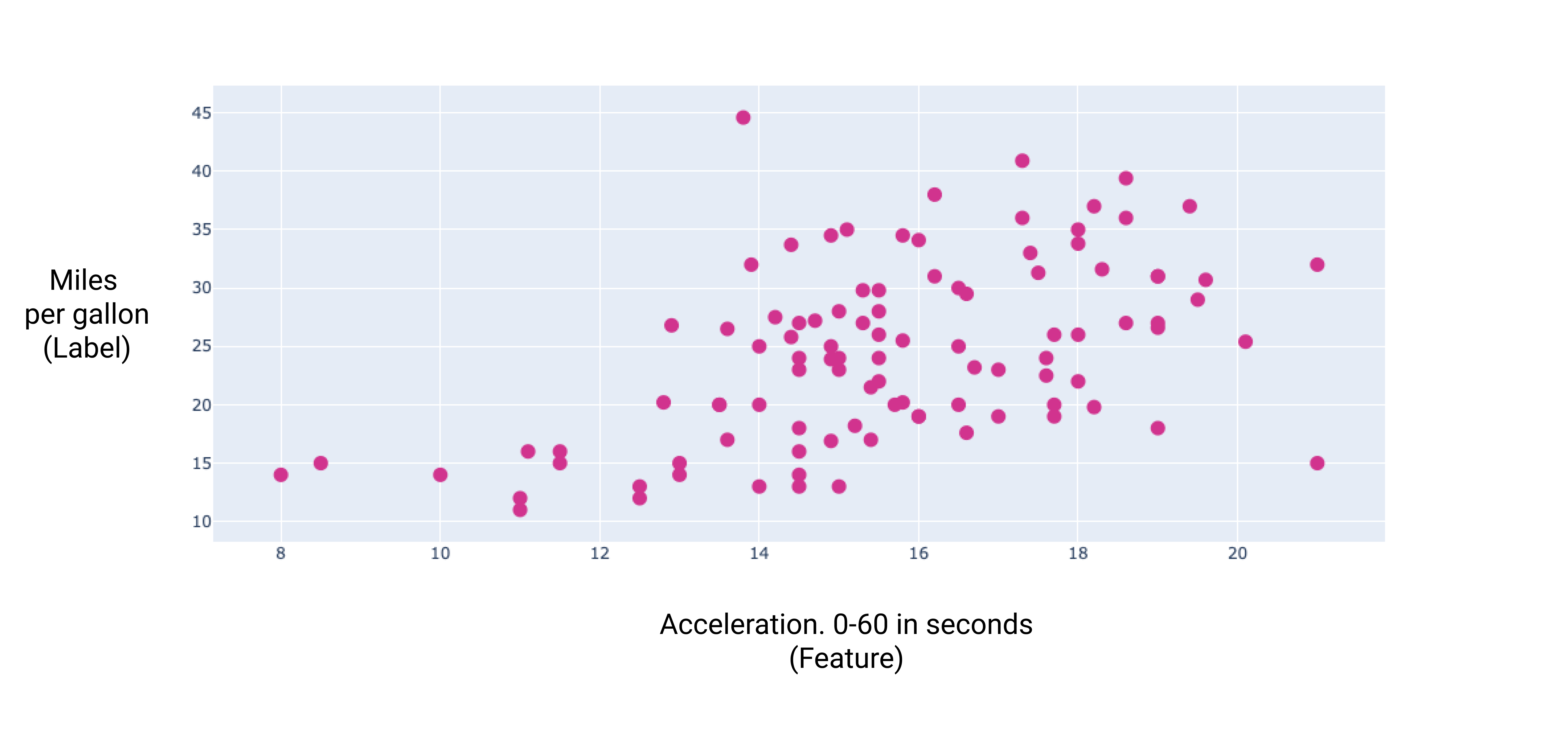
Abbildung 7. Die Beschleunigung eines Autos und die Lesbarkeit von Kilometern pro Gallone. Da das Autofahren dauert die Beschleunigung länger.
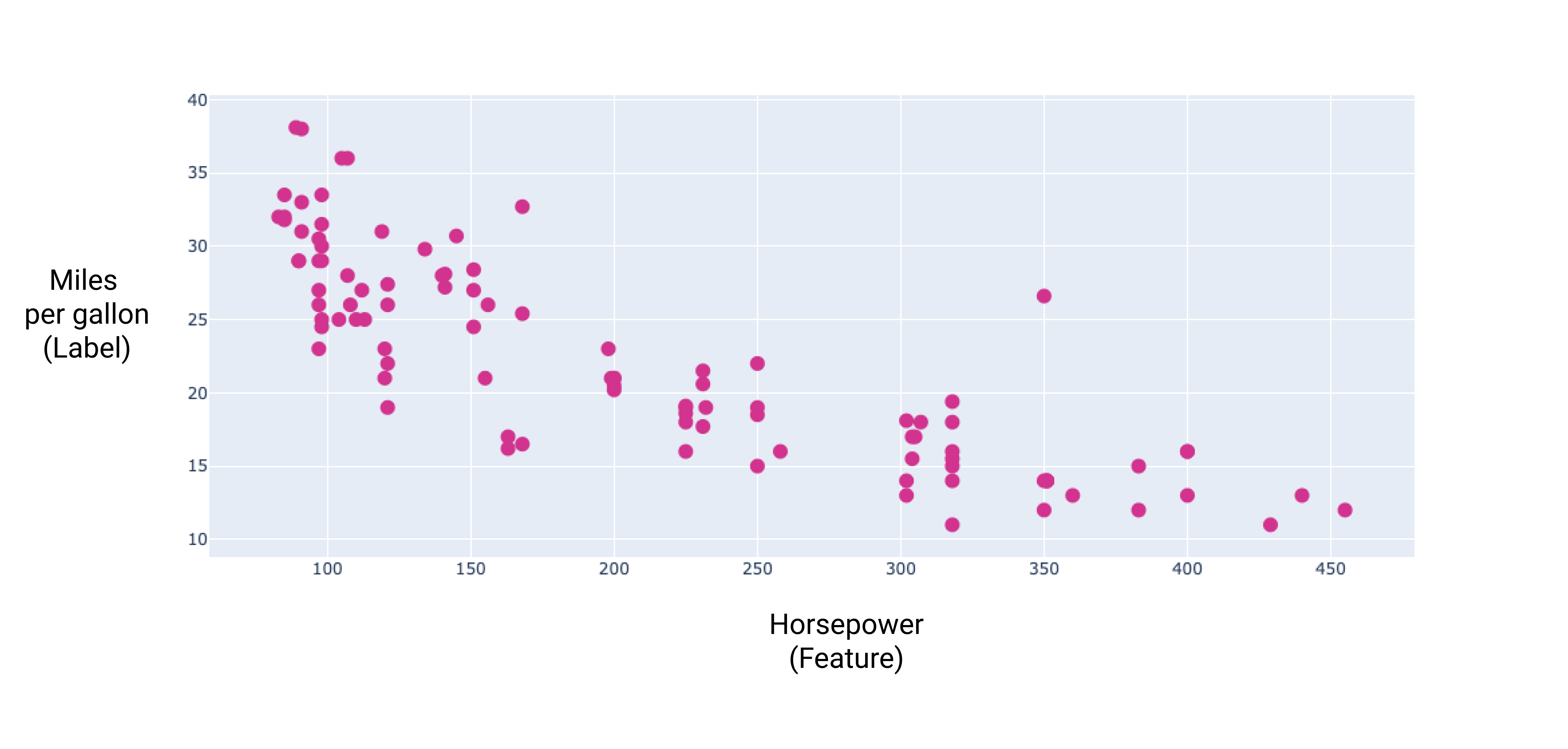
Abbildung 8. Die PS und die Meilen pro Gallone. Da das Autofahren PS-Wert steigt, sinkt die Leistung in Kilometern pro Gallone.
