במודול הזה נסביר את העקרונות של רגרסיה לינארית.
רגרסיה לינארית היא טכניקה סטטיסטית שמשמשת לזיהוי הקשר בין משתנים. בהקשר של למידת מכונה, רגרסיה לינארית מאפשרת למצוא את הקשר בין מאפיינים לבין תוויות.
לדוגמה, נניח שאנחנו רוצים לחזות את יעילות הדלק של רכב במונחי מייל לגלון על סמך המשקל של הרכב, ויש לנו את מערך הנתונים הבא:
| פאונד באלפים (תכונה) | מיילים לגלון (תווית) |
|---|---|
| 3.5 | 18 |
| 3.69 | 15 |
| 3.44 | 18 |
| 3.43 | 16 |
| 4.34 | 15 |
| 4.42 | 14 |
| 2.37 | 24 |
אם נציב את הנקודות האלה בתרשים, נקבל את התרשים הבא:
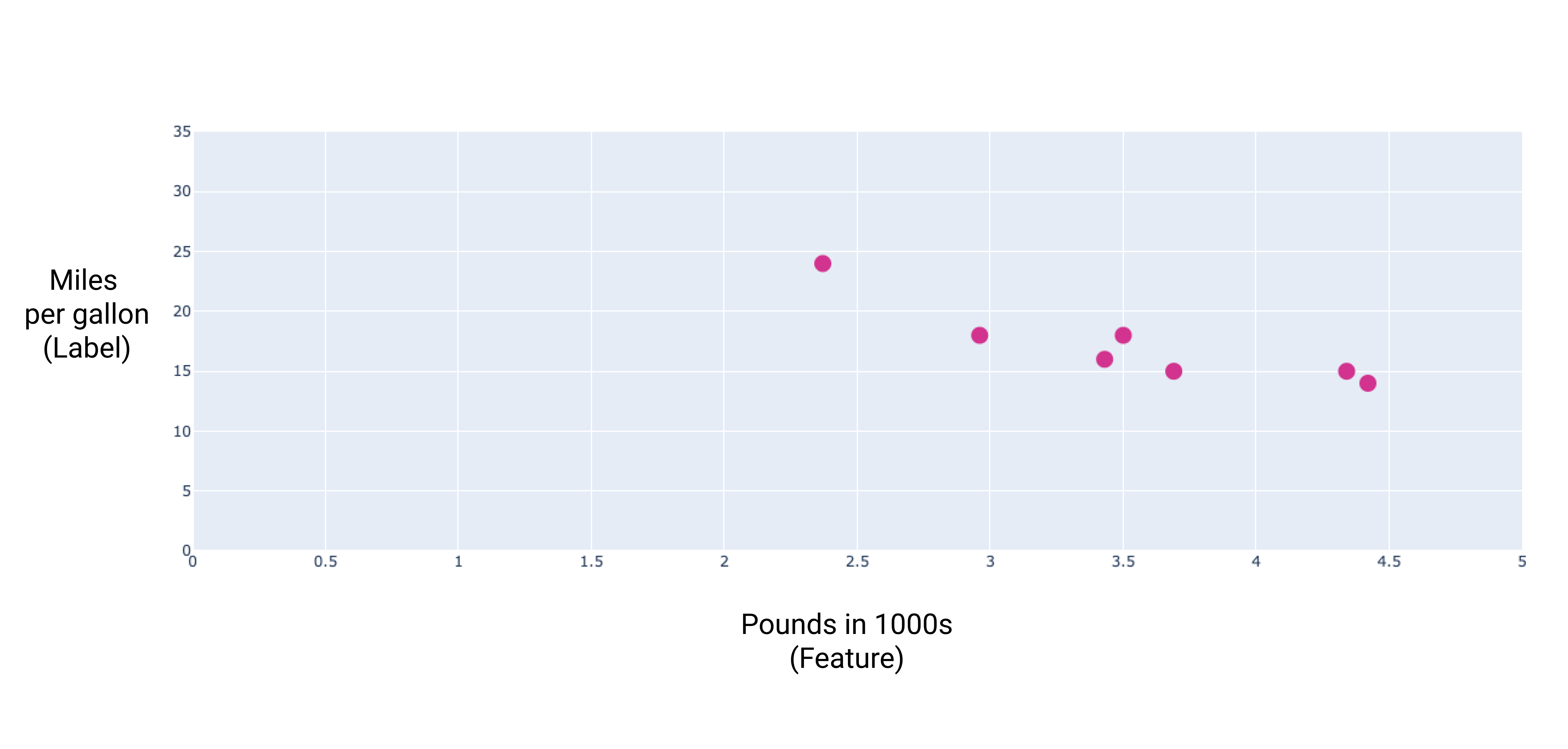
איור 1. משקל הרכב (בליברות) לעומת דירוג המיילים לגלון. ככל שהרכב כבד יותר, בדרך כלל מדד הקילומטרים לליטר שלו יורד.
אפשר ליצור מודל משלכם על ידי ציור קו התאמה הכי טוב דרך הנקודות:
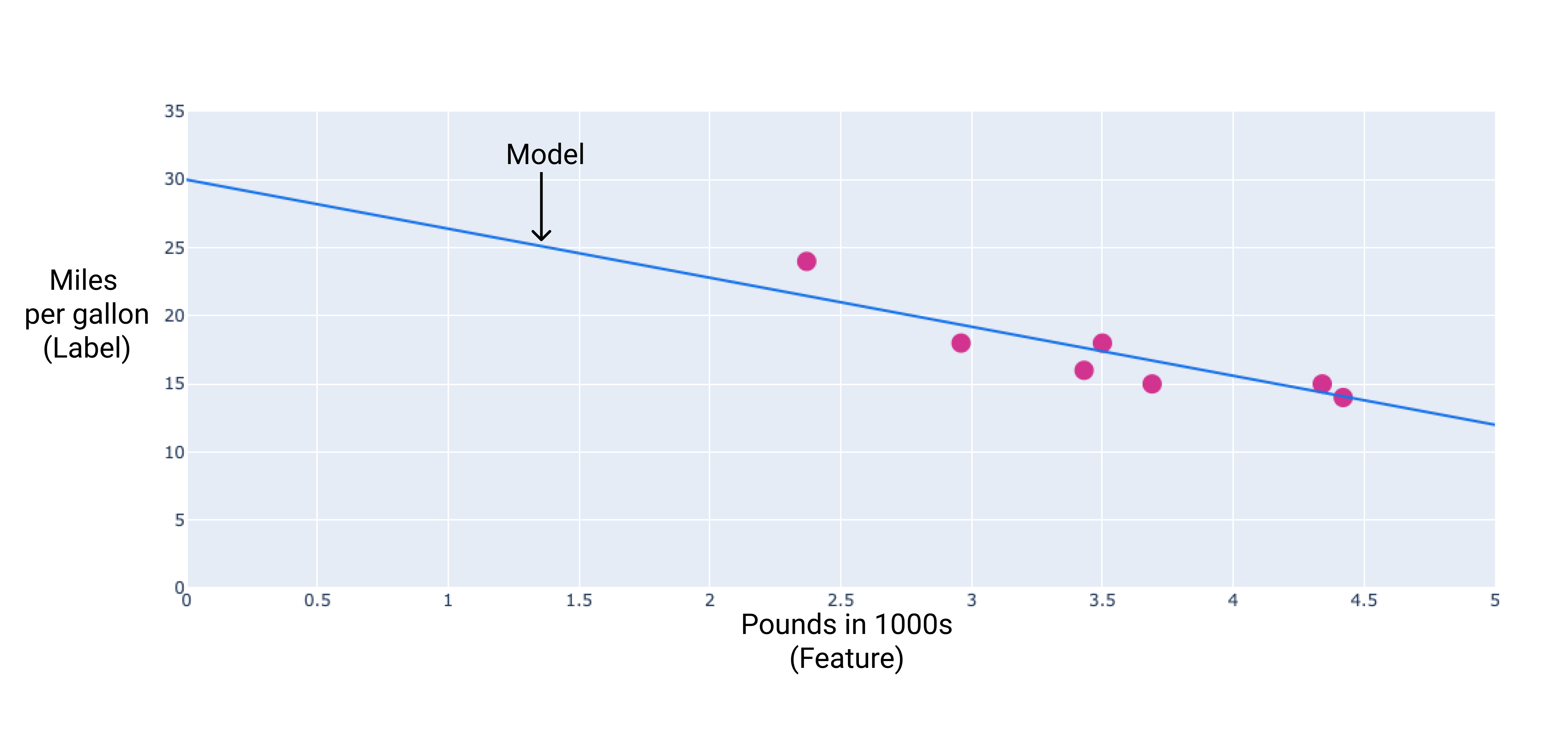
איור 2. קו התאמה מושלם שעבר דרך הנתונים מהתרשים הקודם.
משוואת רגרסיה ליניארית
במונחים אלגבריים, המודל מוגדר כ- $ y = mx + b $, כאשר
- הערך $y $ הוא מייל לגלון – הערך שאנחנו רוצים לחזות.
- m הוא השיפוע של הקו.
- $ x $ הוא ליש – ערך הקלט שלנו.
- הערך $b $ הוא נקודת החיתוך עם ציר y.
ב-ML, כותבים את המשוואה של מודל רגרסיה ליניארית באופן הבא:
where:
- הערך $ y' $ הוא התווית החזויה – הפלט.
- הערך $ b $ הוא הטיה של המודל. הטיה היא אותו מושג כמו נקודת החיתוך עם ציר y בנוסחה האלגברית של קו. בלמידת מכונה, לפעמים מכנים את ההטיה בשם $ w_0 $. ההטיה היא פרמטר של המודל, והיא מחושבת במהלך האימון.
- הערך $ w_1 $ הוא המשקל של המאפיין. המשקל הוא אותו מושג כמו השיפוע m בנוסחה האלגברית של קו. המשקל הוא פרמטר של המודל, והוא מחושב במהלך האימון.
- $ x_1 $ הוא מאפיין – הקלט.
במהלך האימון, המודל מחשב את המשקל וההטיה שיוצרים את המודל הטוב ביותר.
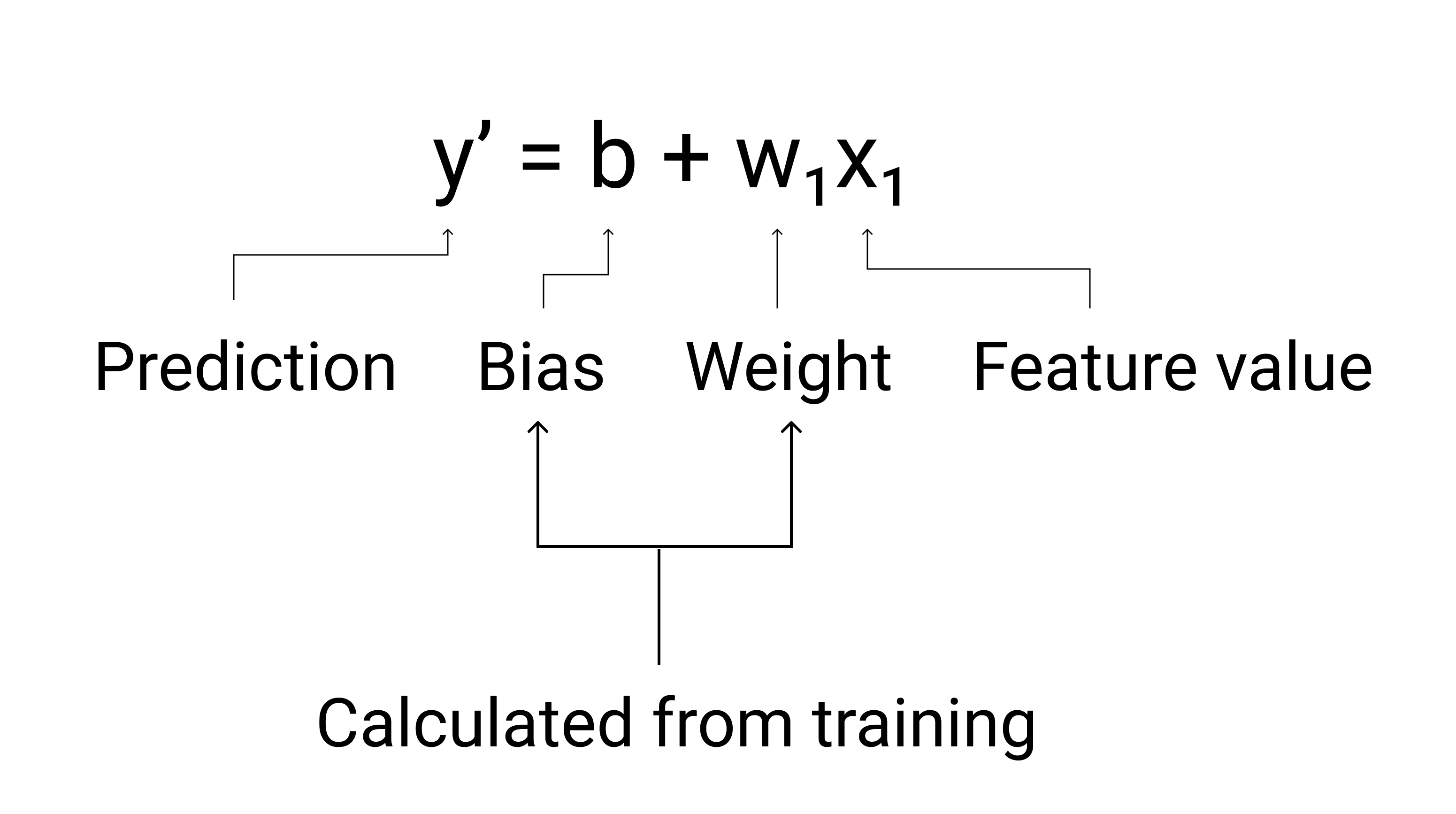
איור 3. ייצוג מתמטי של מודל לינארי.
בדוגמה שלנו, נחשב את המשקל וההטיה מהקו שציירנו. השיפוט הוא 30 (המקום שבו הקו חוצה את ציר ה-Y), והמשקל הוא -3.6 (השיפוע של הקו). המודל יוגדר כ- $ y' = 30 + (-3.6)(x_1) $, ואפשר יהיה להשתמש בו כדי לבצע תחזיות. לדוגמה, לפי המודל הזה, יעילות הדלק הצפויה של רכב במשקל 1,800 ק"ג היא 25.2 ק"מ לליטר.
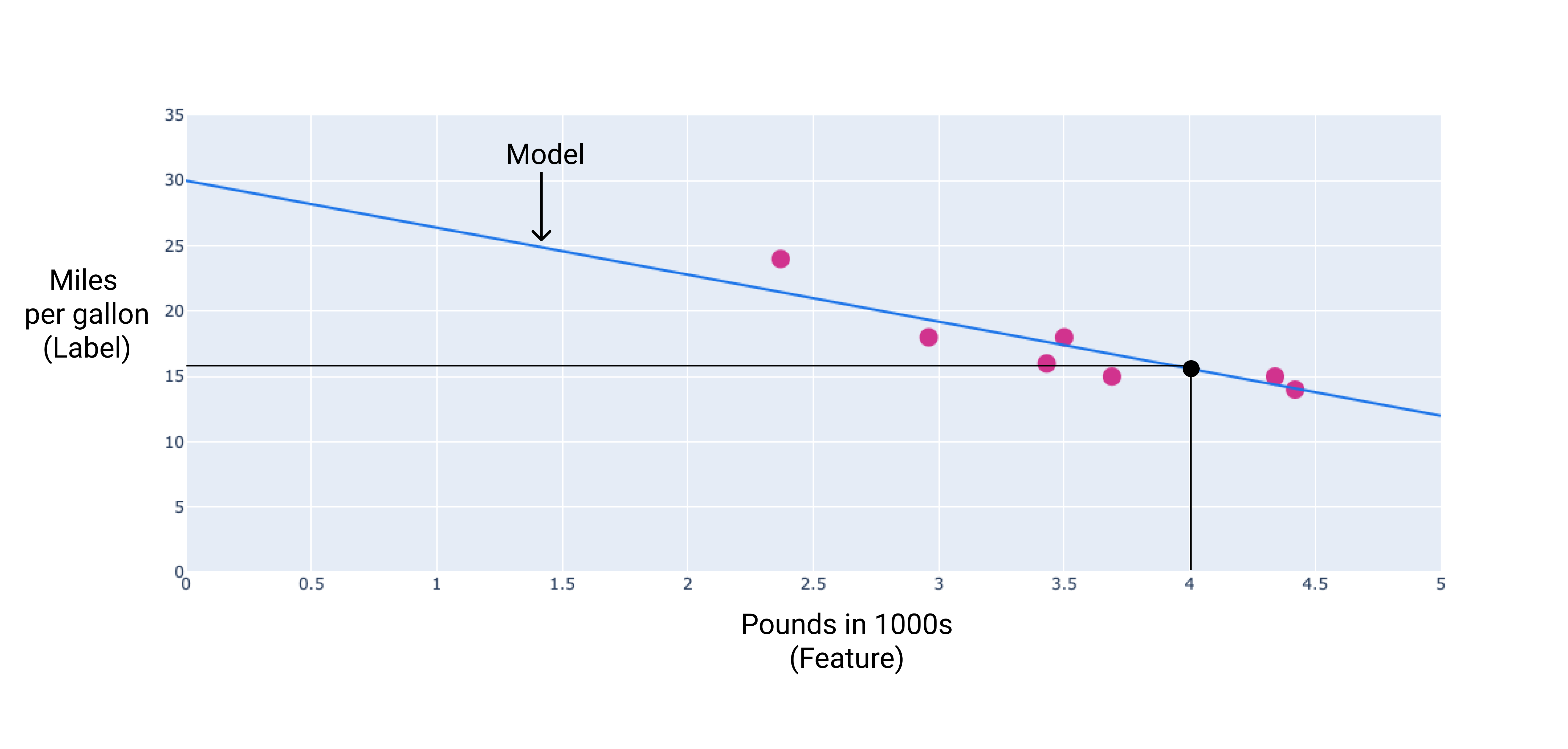
איור 4. לפי המודל, צריכת הדלק הצפויה של רכב במשקל 1,800 ק"ג היא 15.6 מייל לגלון.
מודלים עם כמה תכונות
בדוגמה בקטע הזה נעשה שימוש רק במאפיין אחד – המשקל של הרכב – אבל מודל מתוחכם יותר עשוי להסתמך על כמה מאפיינים, לכל אחד מהם משקל נפרד ($ w_1 $, $ w_2 $ וכו'). לדוגמה, מודל שמבוסס על חמישה מאפיינים ייכתב באופן הבא:
$ y' = b + w_1x_1 + w_2x_2 + w_3x_3 + w_4x_4 + w_5x_5 $
לדוגמה, מודל לחיזוי צריכת דלק יכול להשתמש גם בתכונות כמו:
- נפח מנוע
- האצה
- מספר הצילינדרים
- כוח סוס
המודל הזה ייכתב כך:
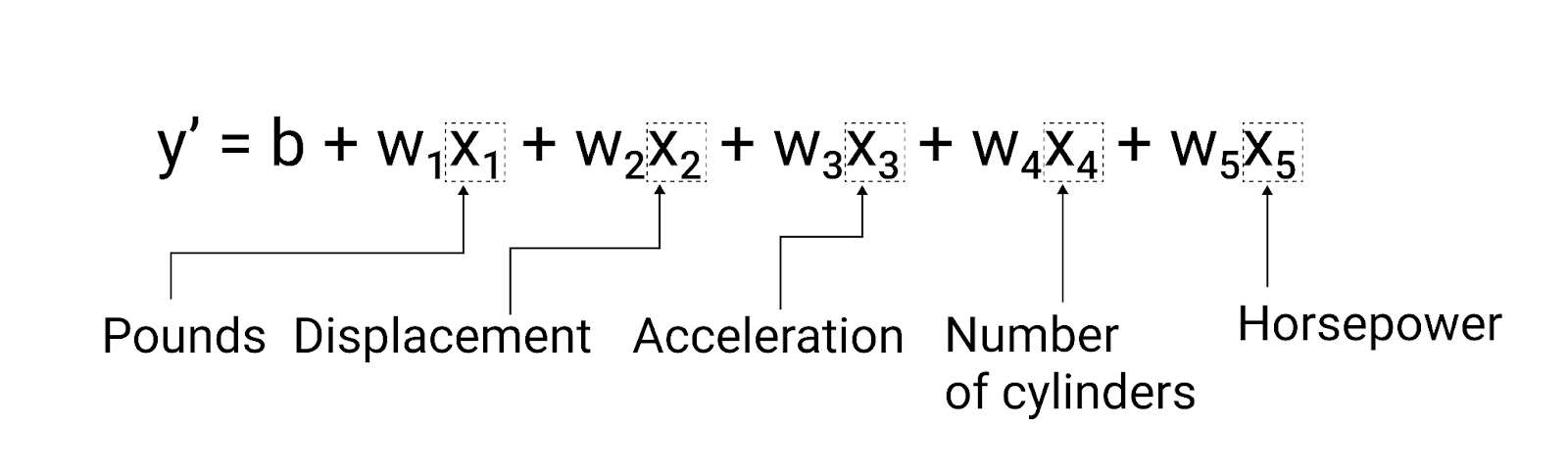
איור 5. מודל עם חמישה מאפיינים לחיזוי הדירוג של רכב לפי מיילים לגלון.
כשמציגים בתרשים חלק מהתכונות הנוספות האלה, אפשר לראות שיש להן גם יחס לינארי לתוויות, מייל לליטר:
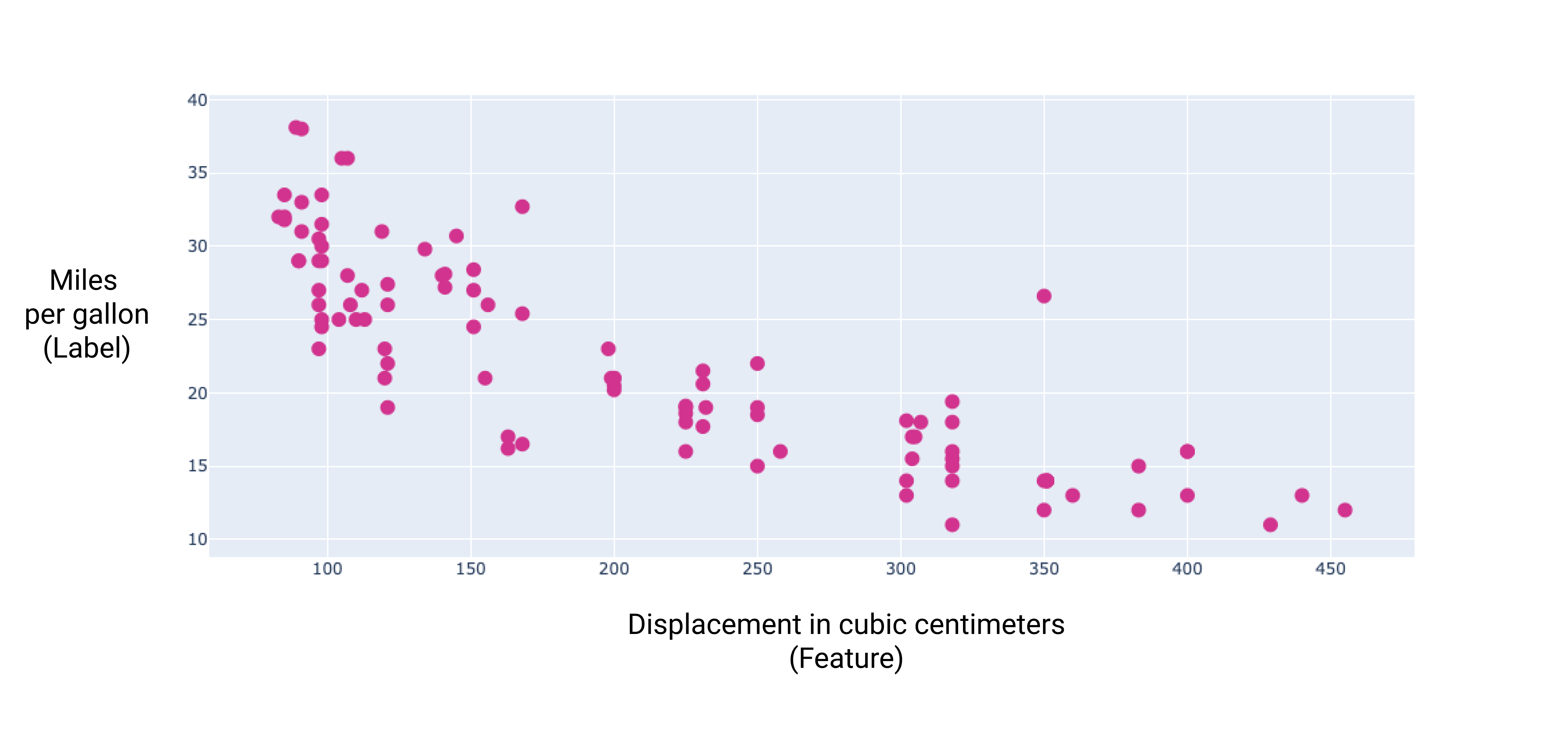
איור 6. נפח המנוע בסנטימטרים מעוקבים והדירוג של המכונית לפי מיילים לגלון. ככל שמנוע הרכב גדול יותר, בדרך כלל יעילות הדלק שלו קטנה יותר.
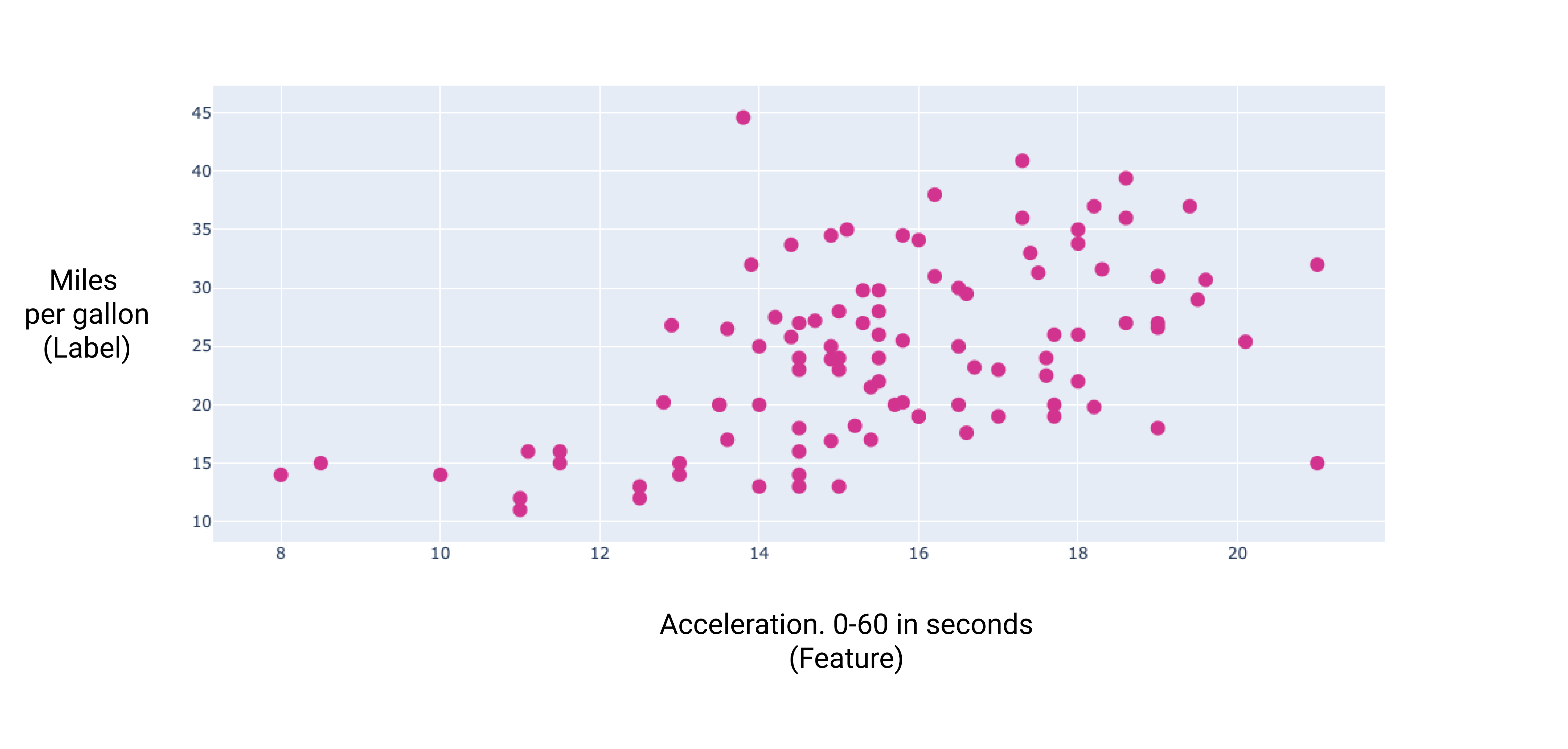
איור 7. ההאצה של הרכב והדירוג שלו לפי מיילים לגלון דלק. ככל שהתאוצה של הרכב נמשכת יותר זמן, בדרך כלל מדד הקילומטרים לליטר עולה.
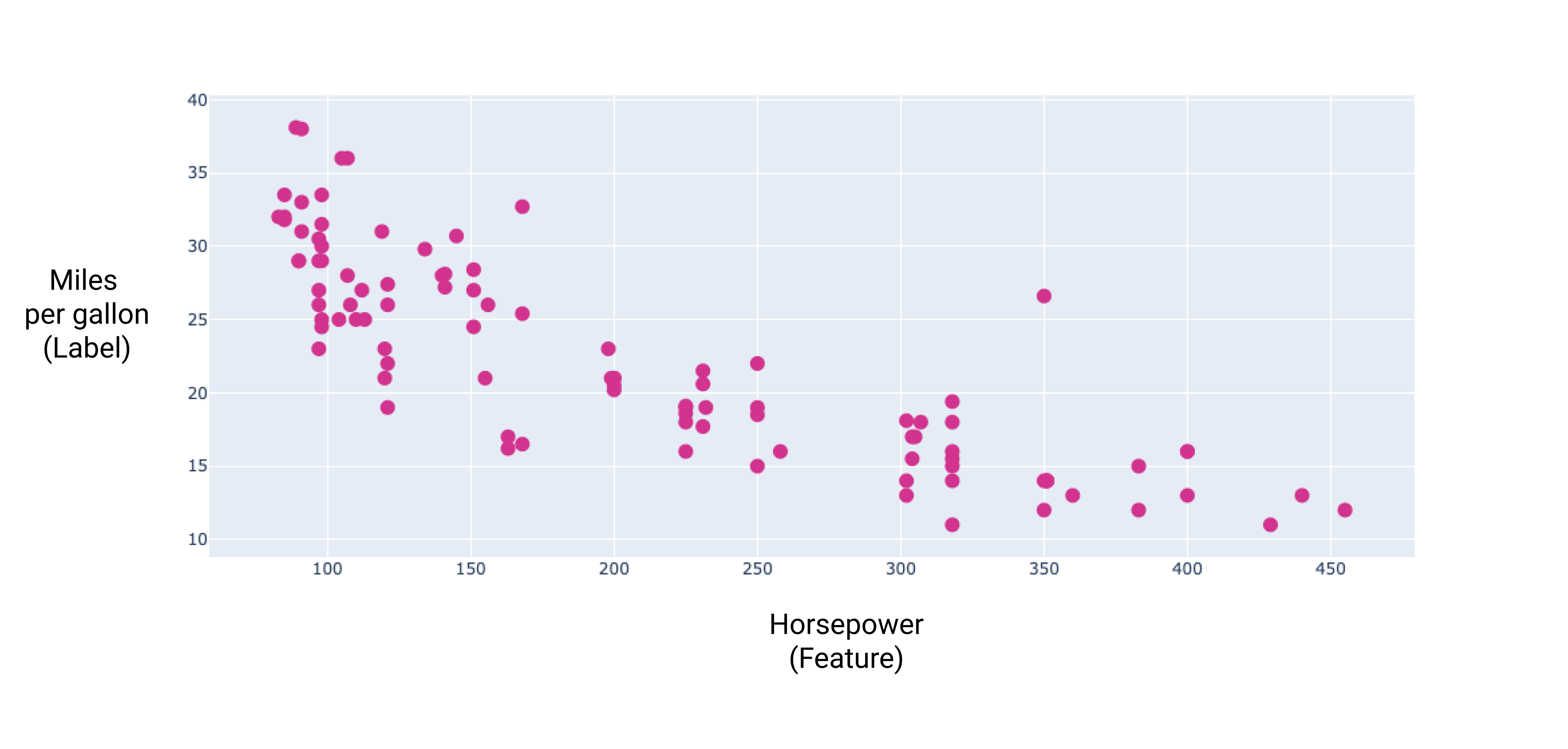
איור 8. כוח הסוס של הרכב והערך של מיילים לגלון דלק. ככל שסוס הכוח של הרכב עולה, בדרך כלל מדד הקילומטרים לליטר יורד.
