本单元介绍线性回归概念。
线性回归是一种 用于找出各个变量之间的关系的统计技术。在机器学习中 线性回归模型会找出 功能和 label。
例如,假设我们要预测汽车的燃油效率(以英里/英里为单位) 根据汽车的重量确定加仑,我们有以下数据集:
| 千磅(功能) | 英里/加仑 (标签) |
|---|---|
| 3.5 | 18 |
| 3.69 | 15 |
| 3.44 | 18 |
| 3.43 | 16 |
| 4.34 | 15 |
| 4.42 | 14 |
| 2.37 | 24 |
如果我们绘制这些点,就会得到以下图表:
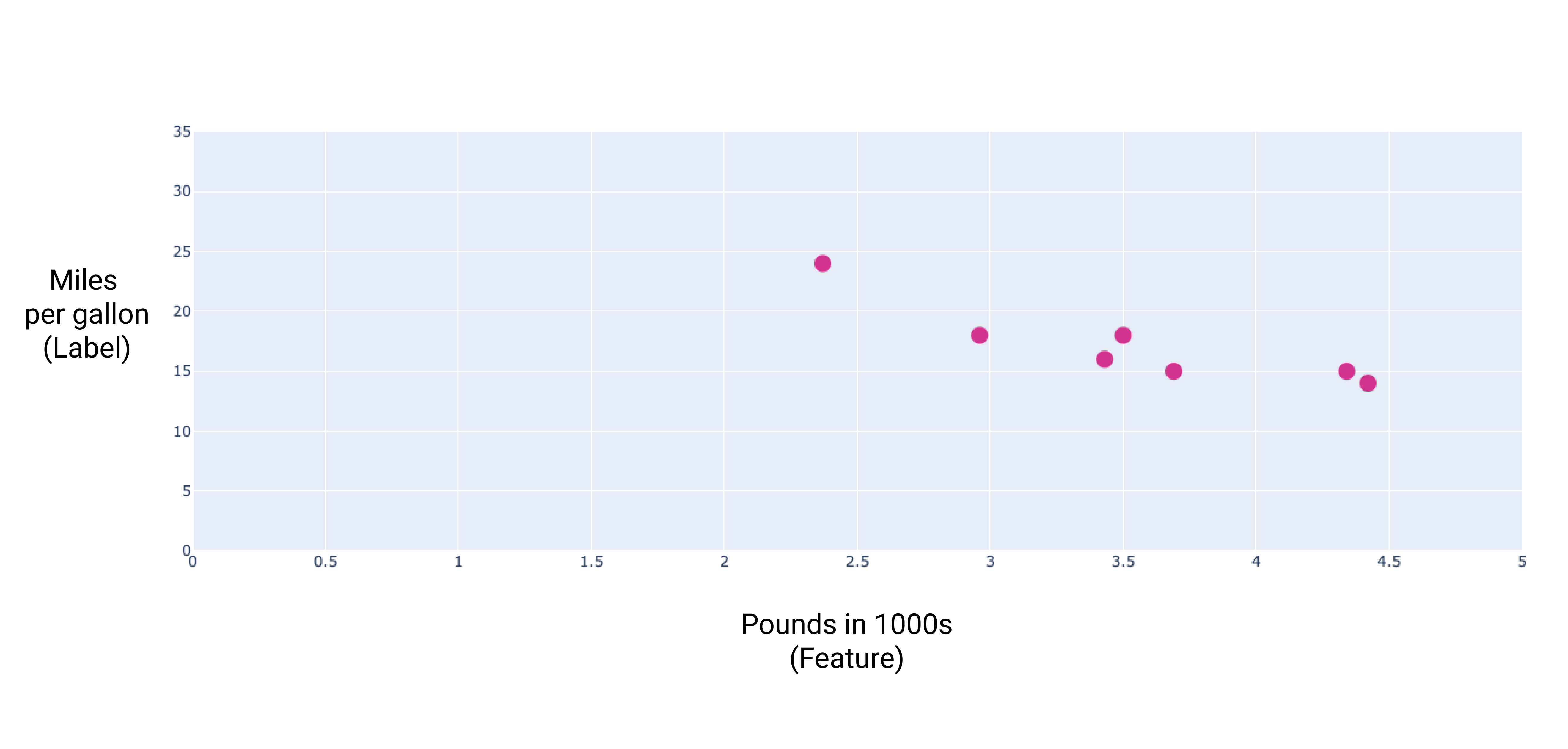
图 1. 汽车重量(以磅为单位)与每加仑英里数的评级。作为 汽车越重,每加仑英里数的评级通常会降低。
我们可以通过这些点绘制一条最适合的直线来创建自己的模型:
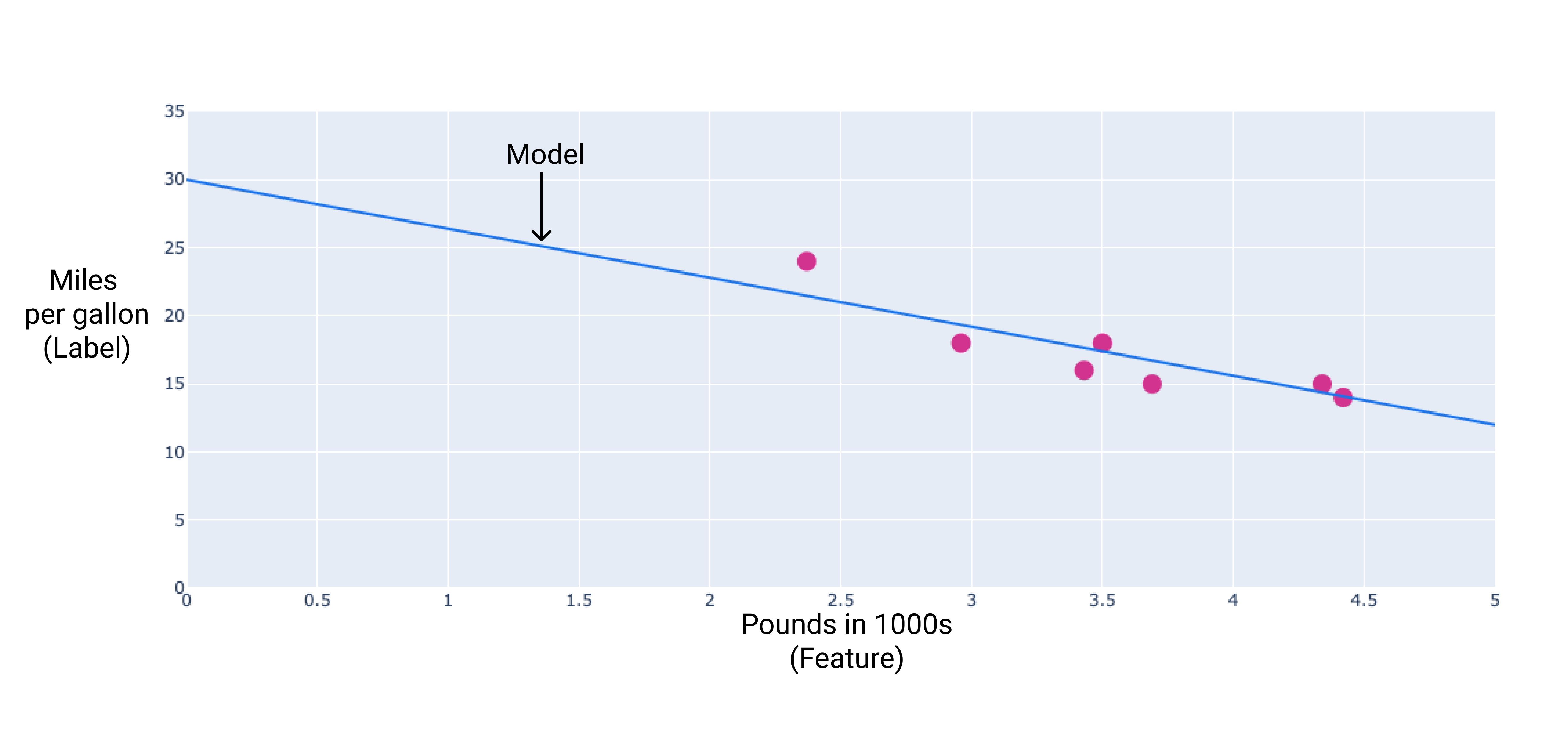
图 2. 上图数据绘制的最适合的线条。
线性回归方程
用代数术语来说,模型的定义为 $ y = mx + b $,其中
- $ y $ 表示每加仑英里数,即我们想要预测的值。
- $ m $ 是直线的斜率。
- $ x $ 是磅,即我们的输入值。
- $ b $ 为 y 轴截距。
在机器学习中,我们编写线性回归模型的方程式,如下所示:
其中:
- $ y'$ 是预测标签,即输出。
- $ b $ 是偏差 模型。偏差与代数中 y 截距的概念相同 直线方程。在机器学习中,偏差有时称为 $ w_0 $。偏差 是一个模型的参数,而 都是在训练期间计算的。
- $ w_1 $ 是权重 功能。权重与代数中斜率 $ m $ 的概念相同 直线方程。权重为 参数,是 在训练期间计算的。
- $ x_1 $ 是一项特征,即 输入。
在训练期间,模型会计算可产生最佳结果的权重和偏差 模型。
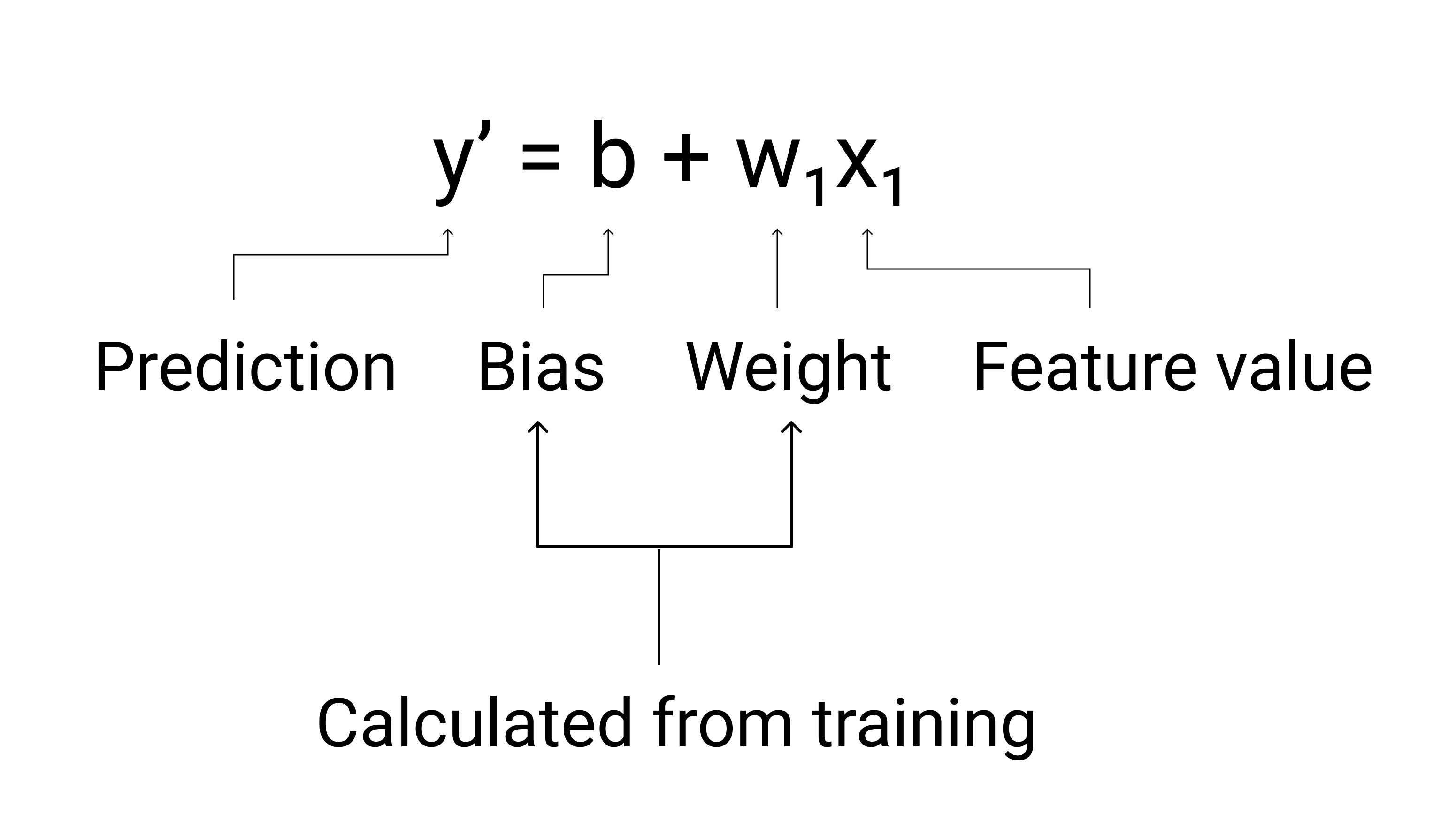
图 3. 线性模型的数学表示法。
在我们的示例中,我们根据绘制的线条计算权重和偏差。通过 偏差为 30(其中直线与 y 轴相交),权重为 -3.6( 直线的斜率)。该模型将定义为 $ y'= 30 + (-3.6)(x_1) $,以及 就可以用它来进行预测了。例如,使用此模型时, 4000 磅的汽车预计燃油效率为每辆 15.6 英里 加仑。
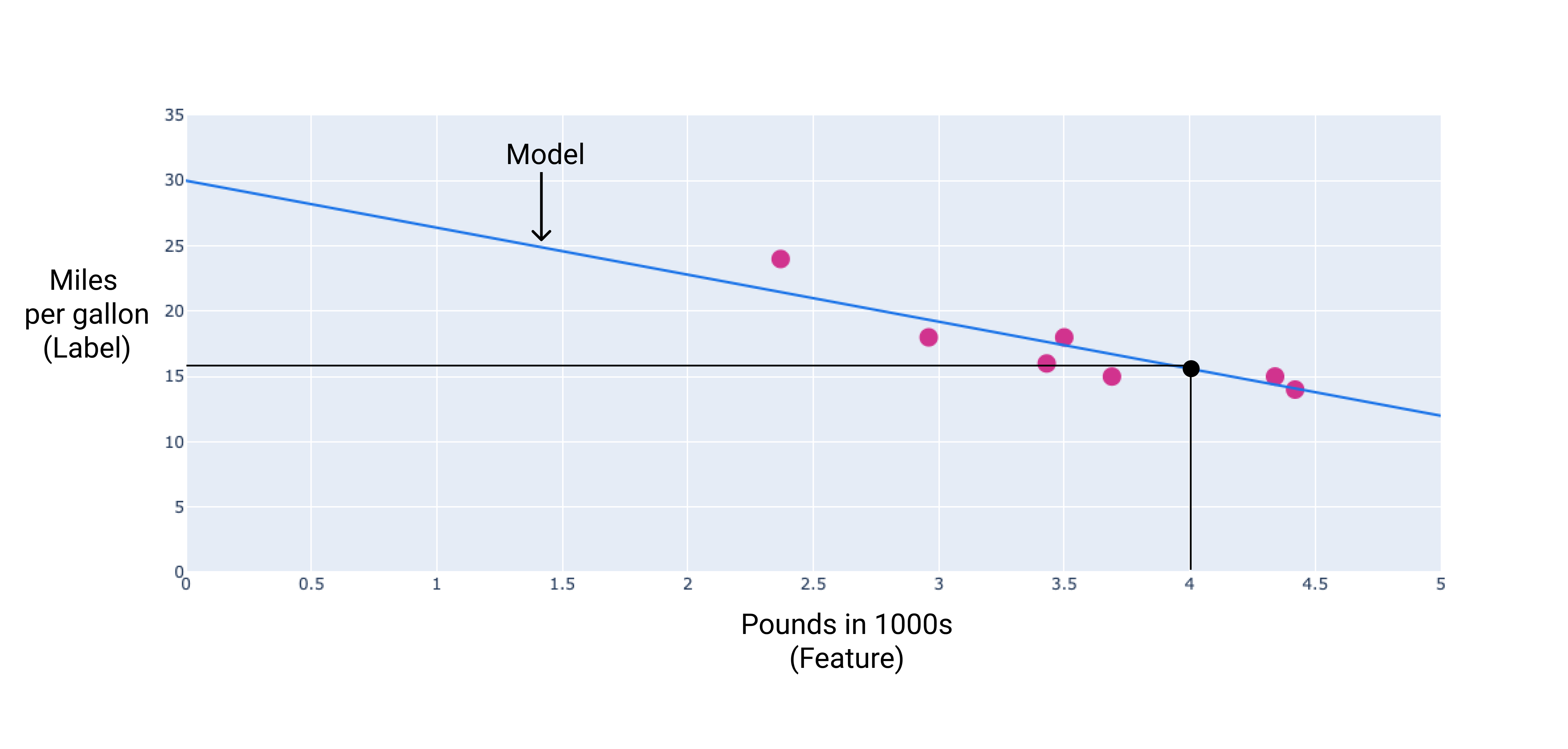
图 4. 使用该模型,一辆 4000 磅重的汽车 燃油效率为每加仑 15.6 英里。
具有多个特征的模型
虽然本部分中的示例仅使用了一项功能,即重量级 汽车的特征,更复杂的模型可能依赖于多种特征, 每个都有单独的重量($ w_1 $、$ w_2 $ 等)。例如,一个模型 可以写如下:
$ y'= b + w_1x_1 + w_2x_2 + w_3x_3 + w_4x_4 + w_5x_5 $
例如,预测汽油里程的模型还可以额外使用特征 例如:
- 发动机排量
- 加速性能
- 汽缸数
- 马力
此模型的编写方式如下:
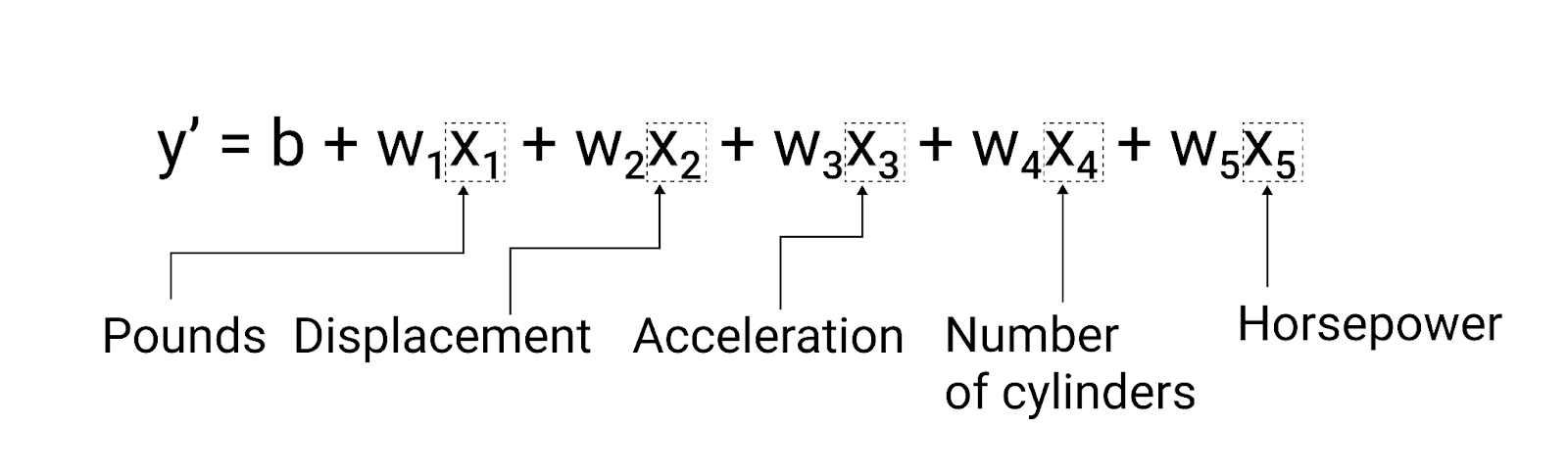
图 5. 一个具有五个特征的模型,用于预测汽车每加仑的英里数 评分。
通过绘制一些附加特征的图表,可以看出它们在 与标签的线性关系(每加仑英里数):
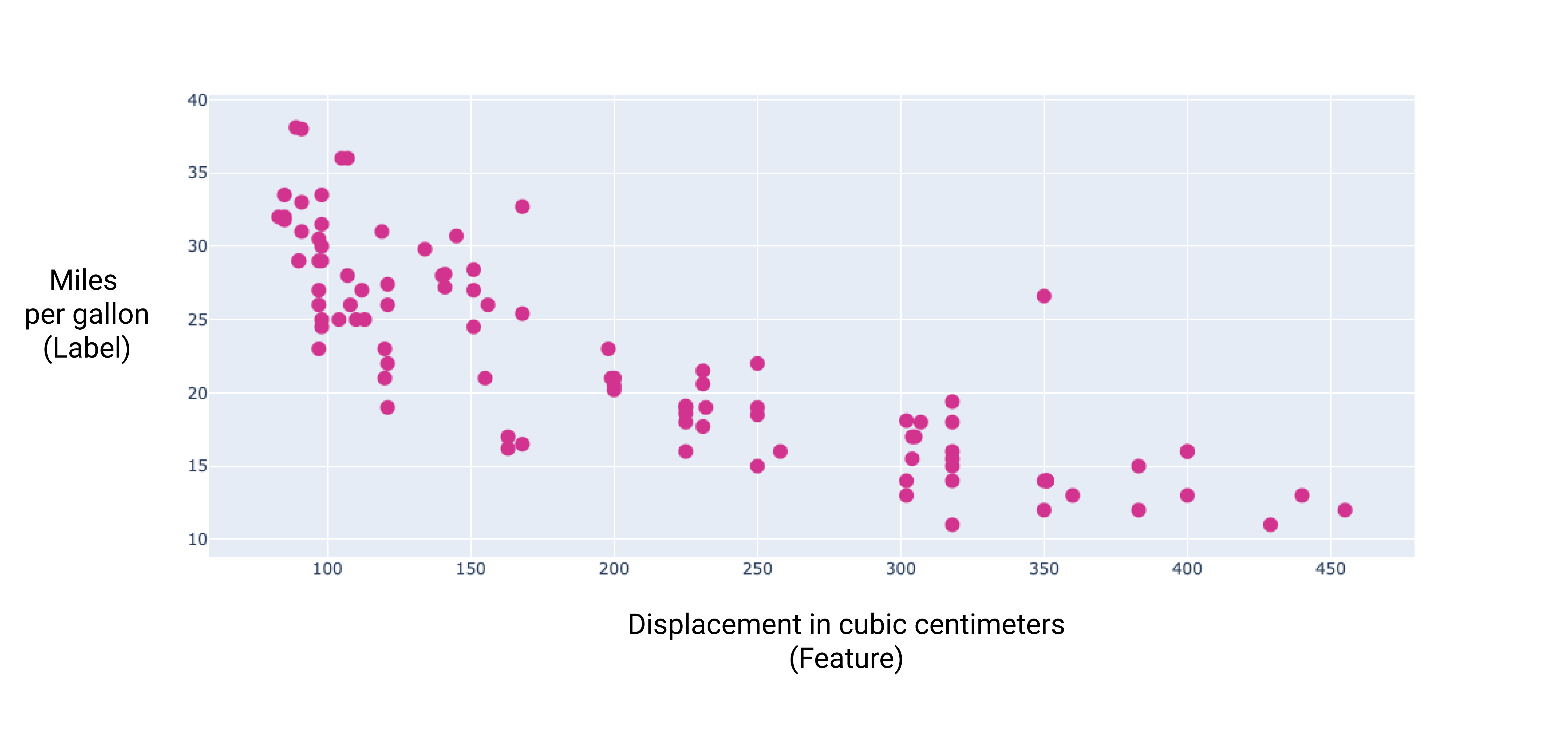
图 6. 汽车的排量(以立方厘米为单位加每加仑的英里数) 评分。汽车的引擎加大了,每加仑的英里数评级通常 。
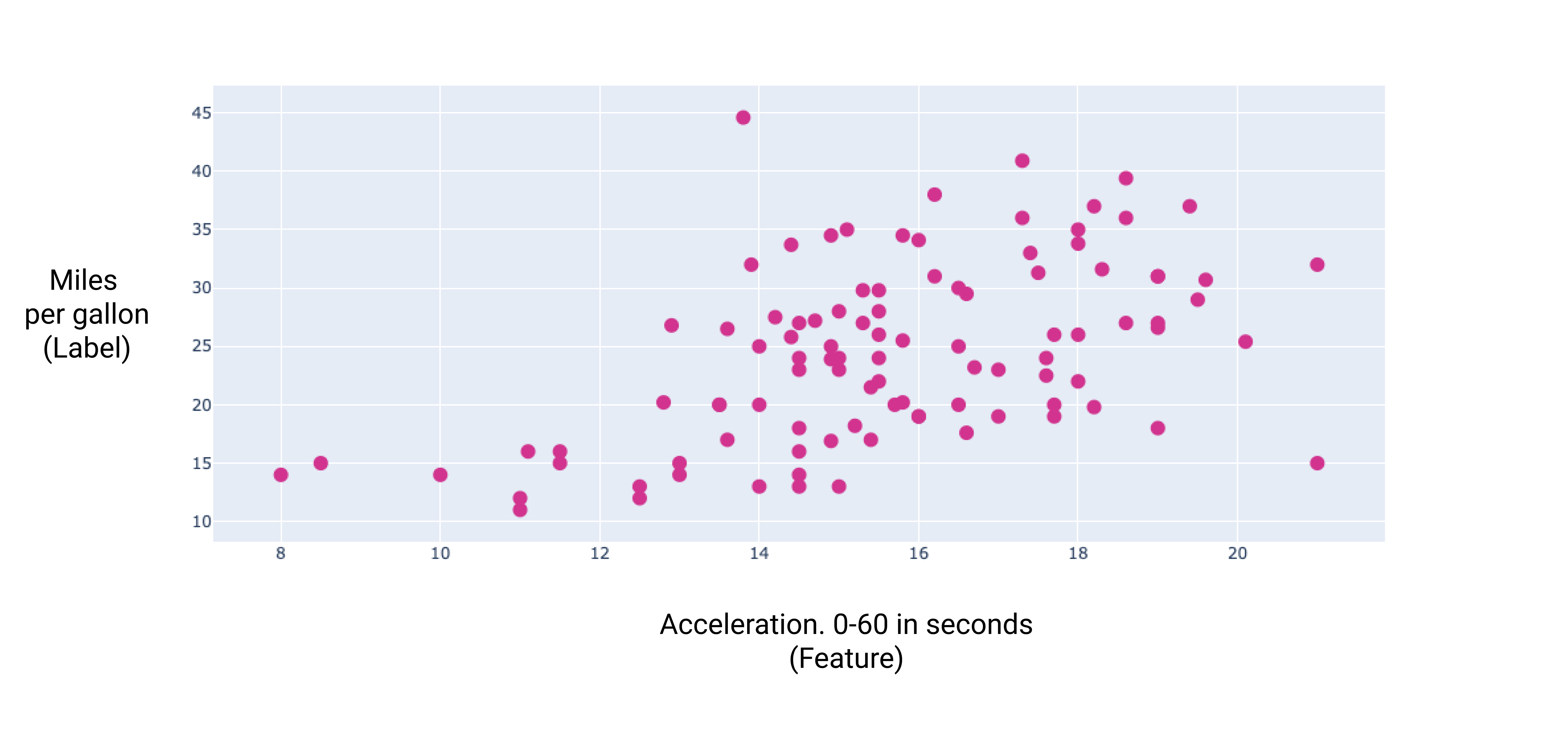
图 7. 汽车的加速度和每加仑英里数的评级。作为汽车 加速用时越长,每加仑英里数的评级通常会提高。
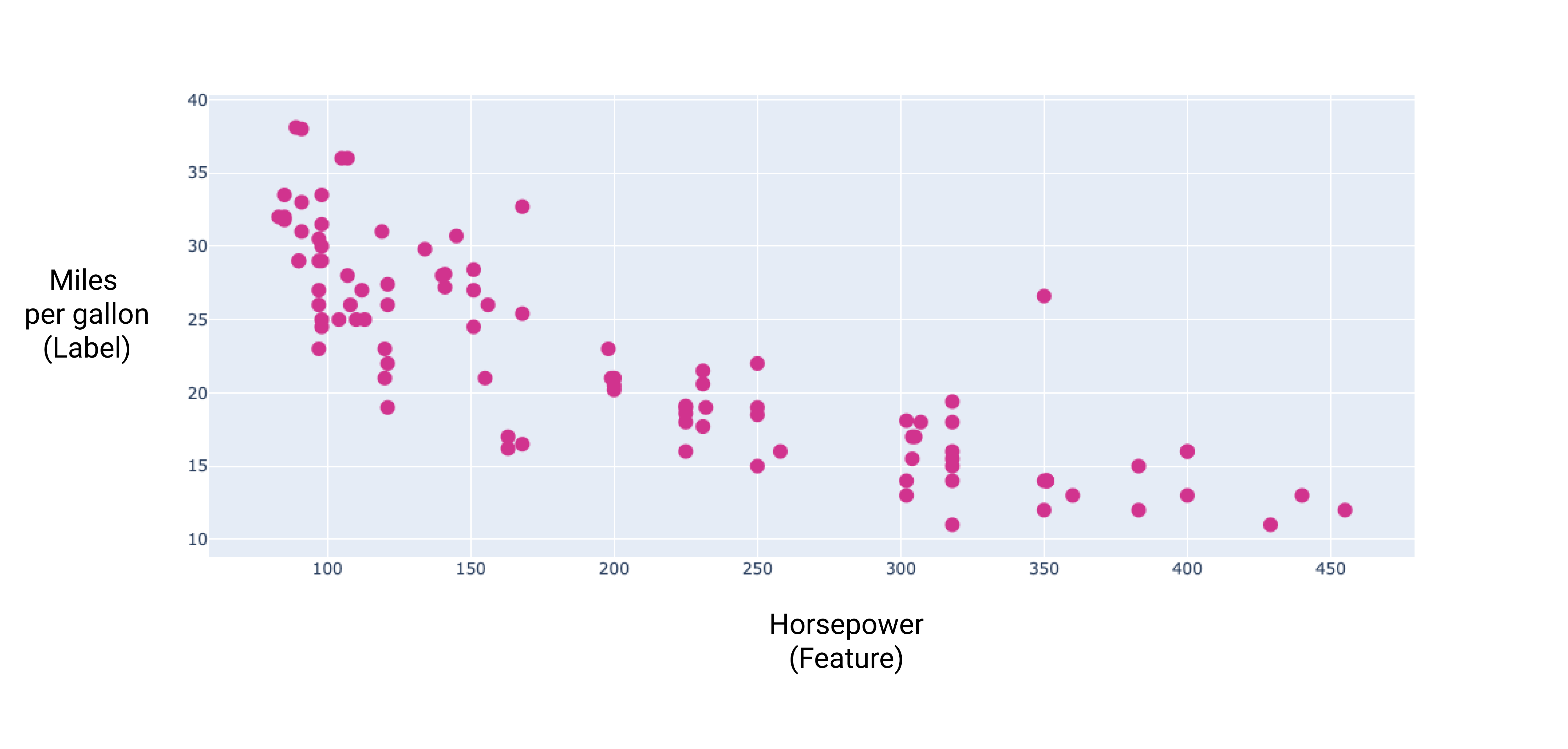
图 8. 汽车的马力和每加仑英里数的评级。作为汽车 马力增加,每加仑英里数的评级通常会降低。
