Neste módulo, apresentamos os conceitos de regressão linear.
A regressão linear é uma técnica estatística para encontrar a relação entre variáveis. Em um modelo de ML contexto, a regressão linear encontra a relação entre recursos e um rótulo.
Por exemplo, suponha que queremos prever a eficiência de combustível de um carro em milhas por litro com base no peso do carro, e temos o seguinte conjunto de dados:
| Libras em milhares (feature) | Milhas por litro (marcador) |
|---|---|
| 3.5 | 18 |
| 3,69 | 15 |
| 3,44 | 18 |
| 3,43 | 16 |
| 4,34 | 15 |
| 4,42 | 14 |
| 2,37 | 24 |
Se plotarmos esses pontos, obteríamos o seguinte gráfico:
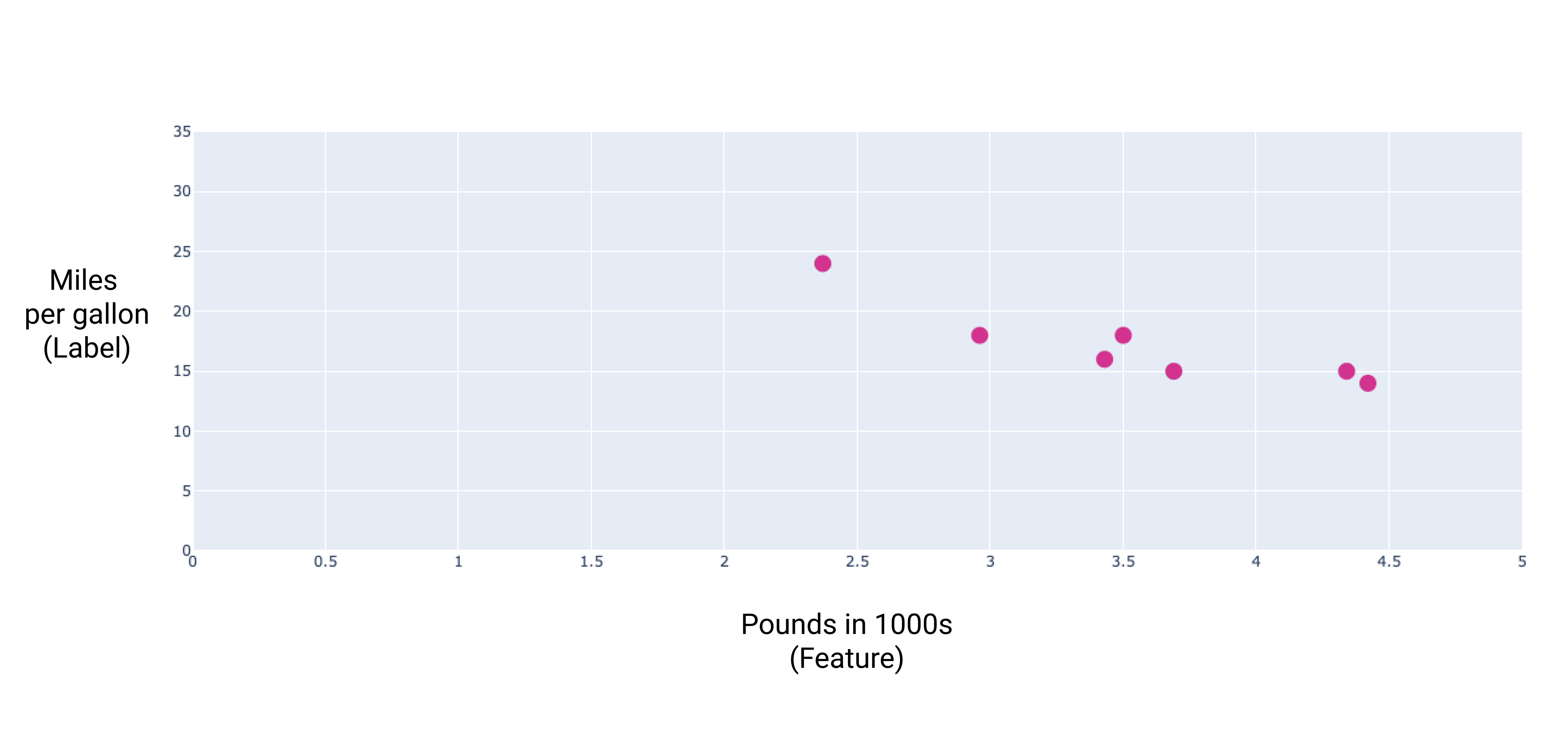
Figura 1. Peso do carro (em libras) versus milhas por galão. Como carro fica mais pesado, a classificação de milhas por litro geralmente diminui.
Podemos criar nosso próprio modelo desenhando uma linha de melhor ajuste pelos pontos:
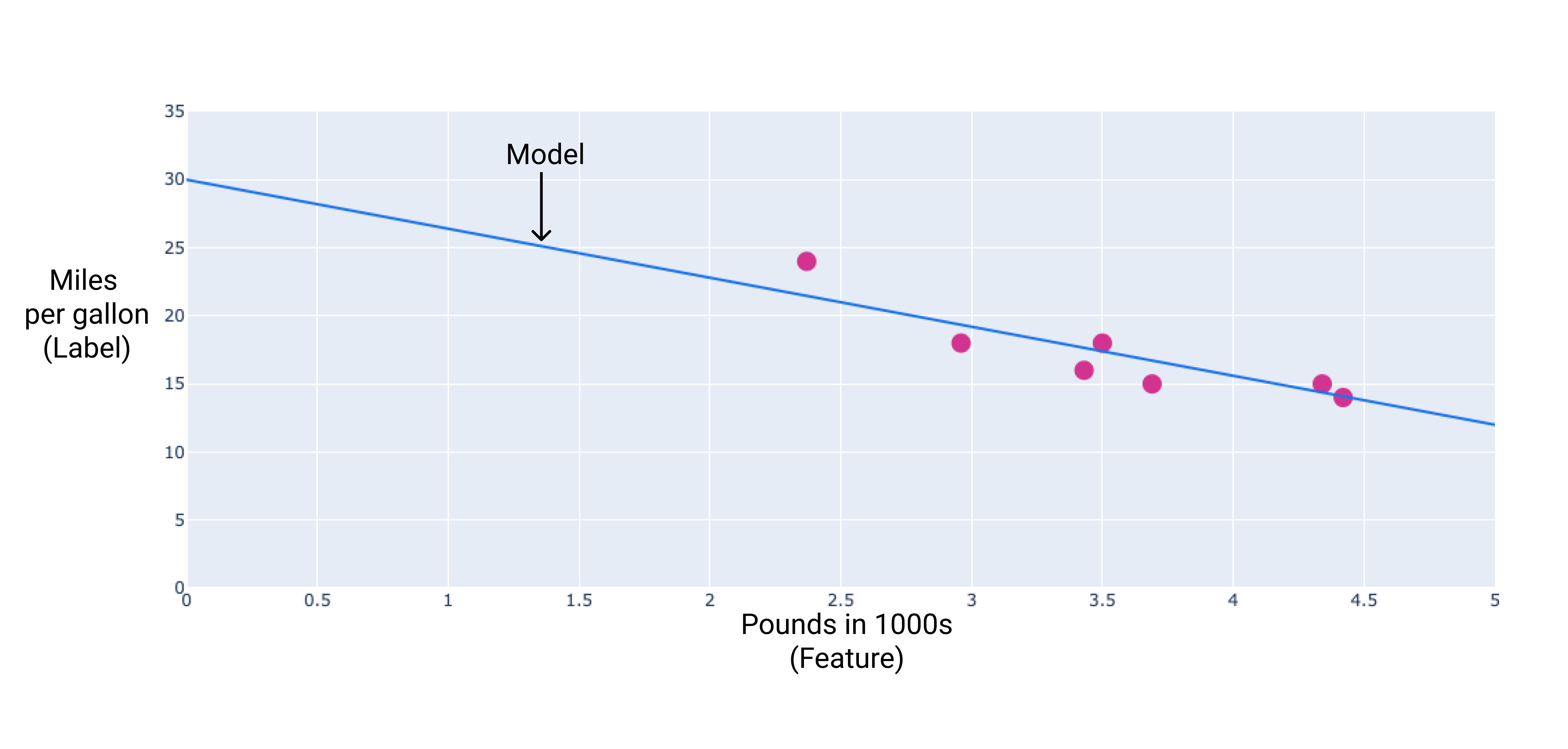
Figura 2. Uma linha de melhor ajuste desenhada pelos dados da figura anterior.
Equação de regressão linear
Em termos algébricos, o modelo seria definido como $ y = mx + b $, em que
- $ y $ são milhas por galão, o valor que queremos prever.
- $ m $ é a inclinação da linha.
- $ x $ é em libras: nosso valor de entrada.
- $ b $ é a interceptação em y.
Em ML, escrevemos a equação de um modelo de regressão linear da seguinte forma:
em que:
- $ y' $ é o rótulo previsto — a saída.
- $ b $ é o viés do modelo. O viés é o mesmo conceito da interceptação y da fórmula de uma linha. Em ML, o viés às vezes é chamado de $ w_0 $. Viés é um parâmetro do modelo e é calculado durante o treinamento.
- $ w_1 $ é o peso do . O peso é o mesmo conceito que a inclinação $ m $ na função algébrica de uma linha. O peso é um parâmetro do modelo e é calculados durante o treinamento.
- $ x_1 $ é um recurso—o entrada.
Durante o treinamento, o modelo calcula o peso e o viés que produzem a melhor um modelo de machine learning.
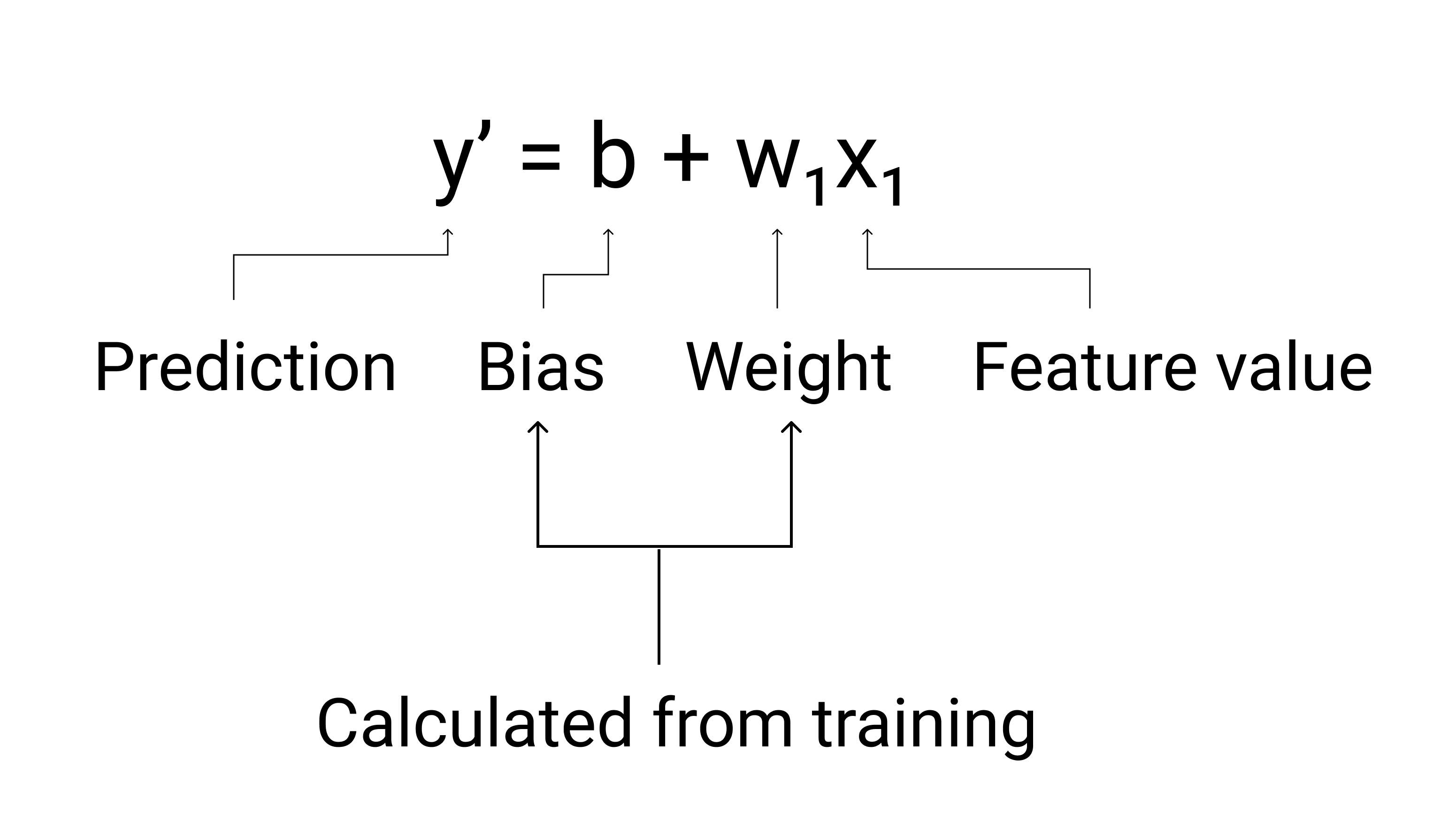
Figura 3. Representação matemática de um modelo linear.
Em nosso exemplo, calcularíamos o peso e o viés a partir da linha que desenhamos. O a tendência é 30 (onde a linha cruza o eixo Y), e o peso é -3,6 (o inclinação da linha). O modelo seria definido como $ y' = 30 + (-3, 6)(x_1) $ e que poderia ser usado para fazer previsões. Por exemplo, usando esse modelo, Um carro de 4.000 libras teria uma eficiência de combustível prevista de 25,6 milhas por litro.
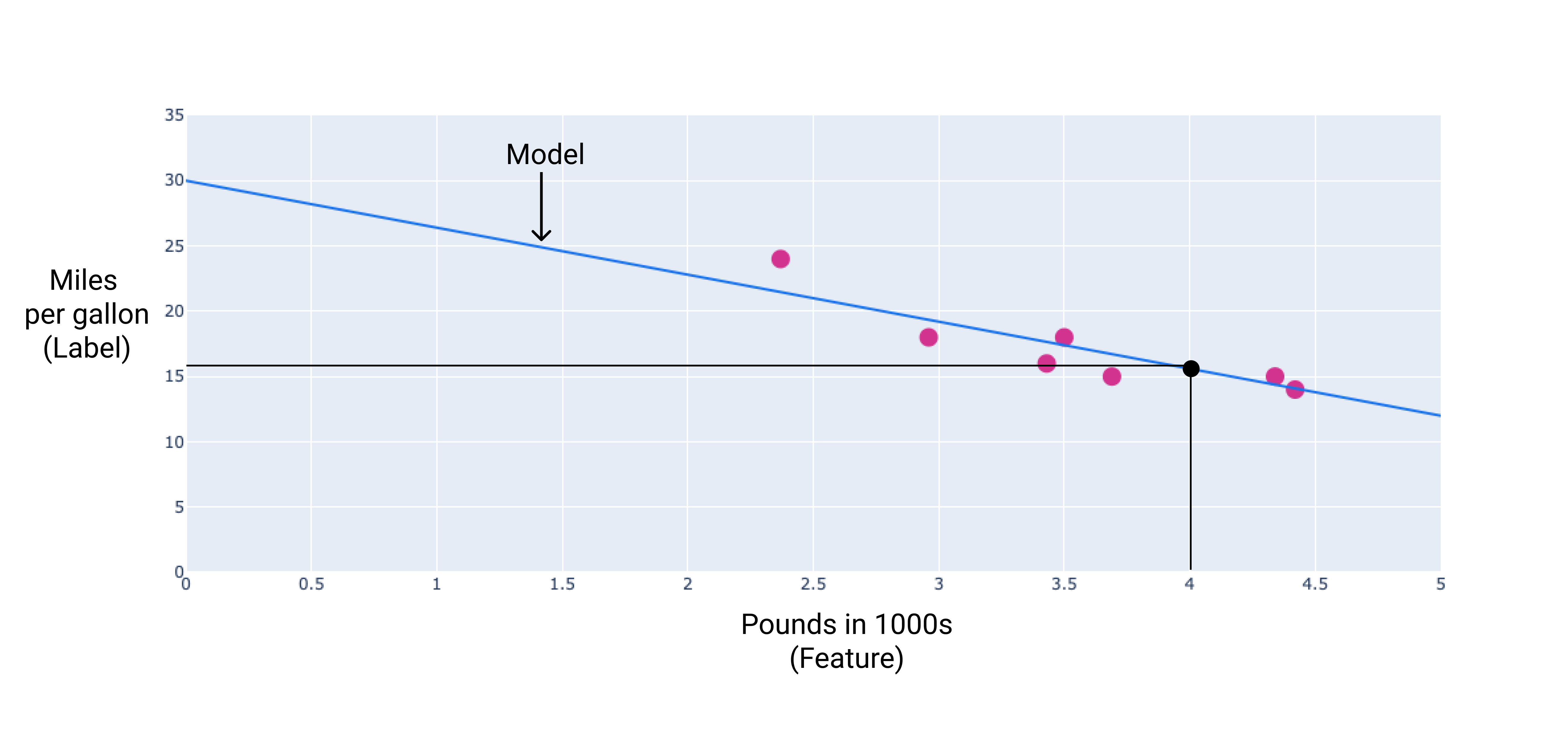
Figura 4. Usando o modelo, um carro de 4.000 libras tem a eficiência de combustível é de 7,2 km por litro.
Modelos com vários recursos
Embora o exemplo desta seção use apenas um recurso, o peso do carro. Um modelo mais sofisticado pode depender de vários recursos, cada um com um peso diferente ($ w_1 $, $ w_2 $ etc.). Por exemplo, um modelo que usa cinco recursos é escrito da seguinte maneira:
$ y' = b + w_1x_1 + w_2x_2 + w_3x_3 + w_4x_4 + w_5x_5 $
Por exemplo, um modelo que prevê a quilometragem de combustível poderia usar atributos adicionalmente como o seguinte:
- Deslocamento do motor
- Aceleração
- Número de cilindros
- Cavalos de potência
Esse modelo seria escrito da seguinte maneira:
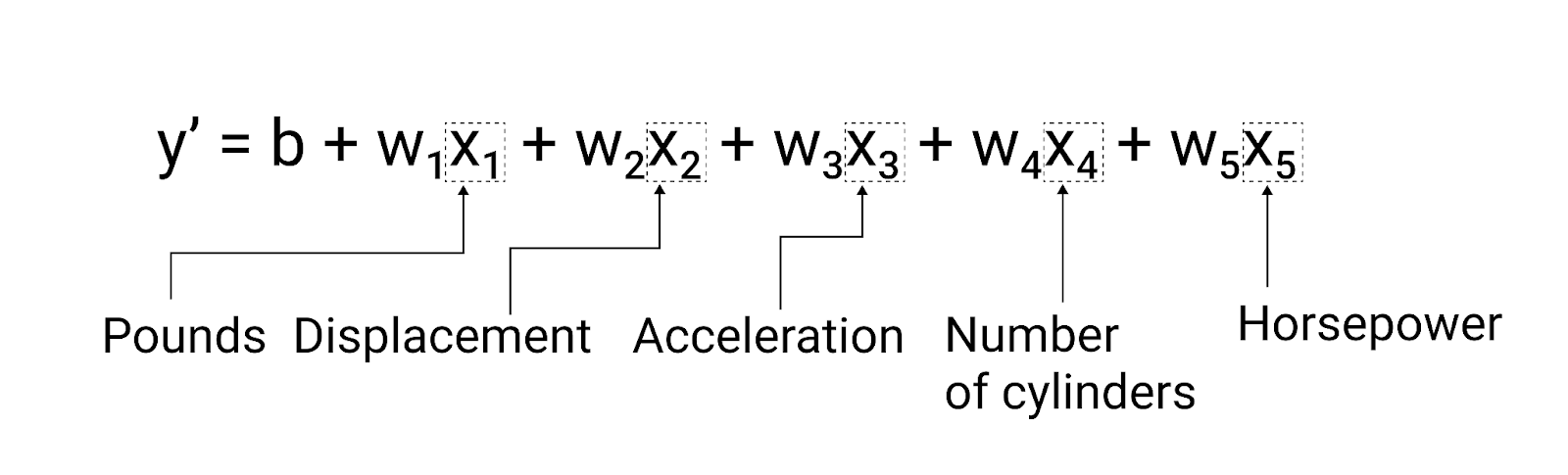
Figura 5. Um modelo com cinco atributos para prever as milhas por litro de um carro classificação.
Ao representar graficamente alguns desses recursos adicionais, podemos ver que eles também têm relação linear com o rótulo, milhas por galão:
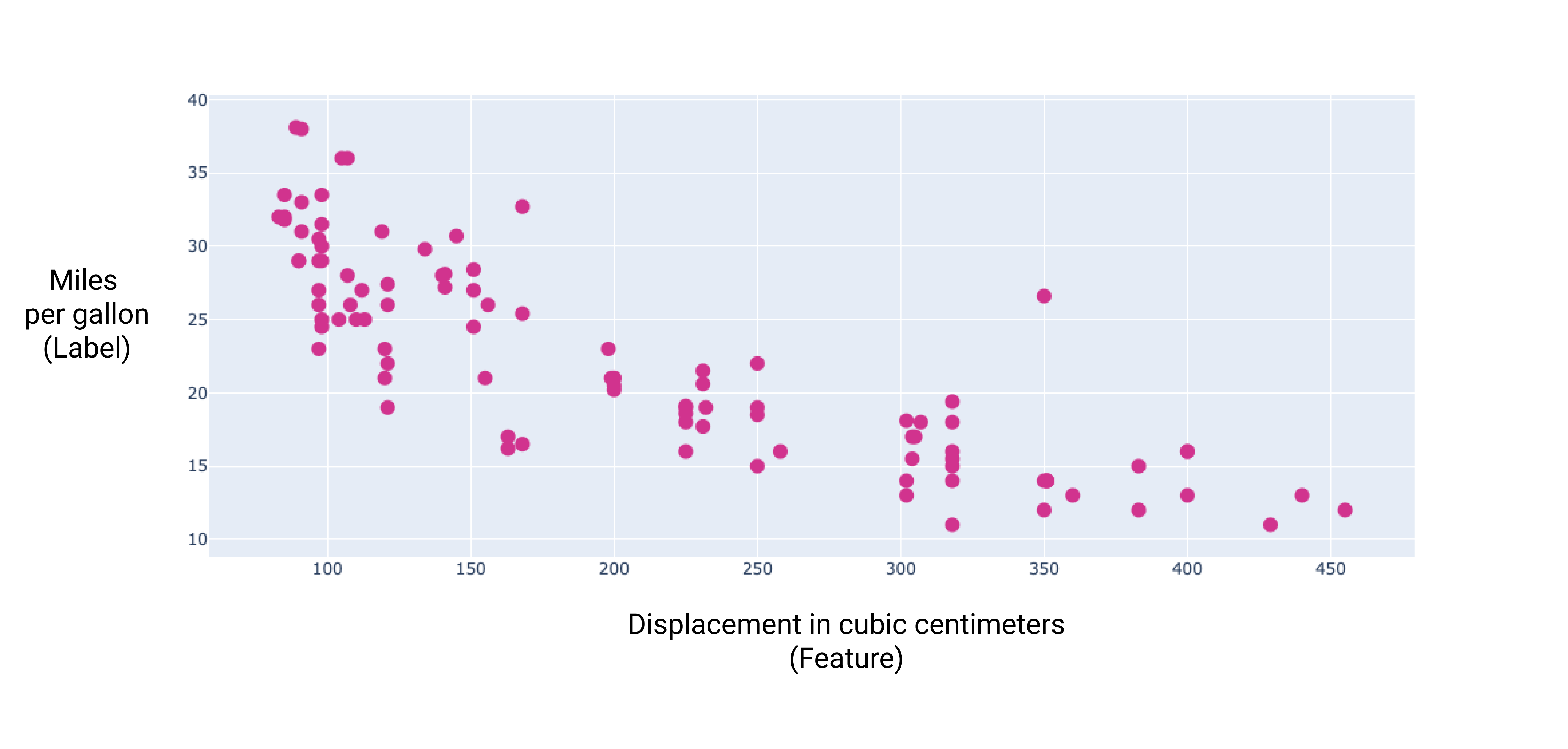
Figura 6. Deslocamento de um carro em centímetros cúbicos e as milhas por litro classificação. À medida que o motor de um carro aumenta, a taxa de milhas por litro geralmente é diminui.
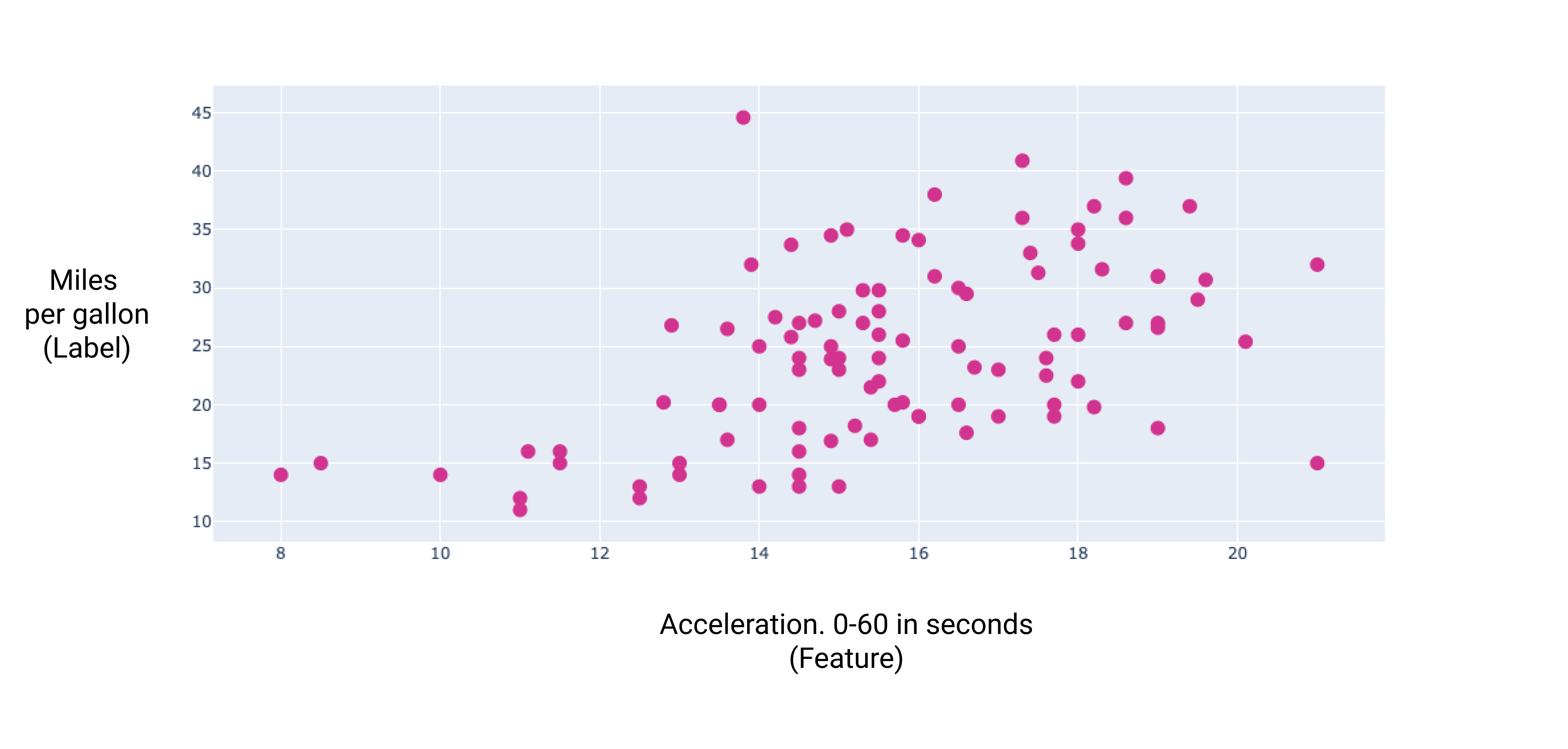
Figura 7. A aceleração de um carro e a taxa de milhas por litro. Como as informações aceleração costuma levar mais tempo, a classificação de milhas por litro geralmente aumenta.
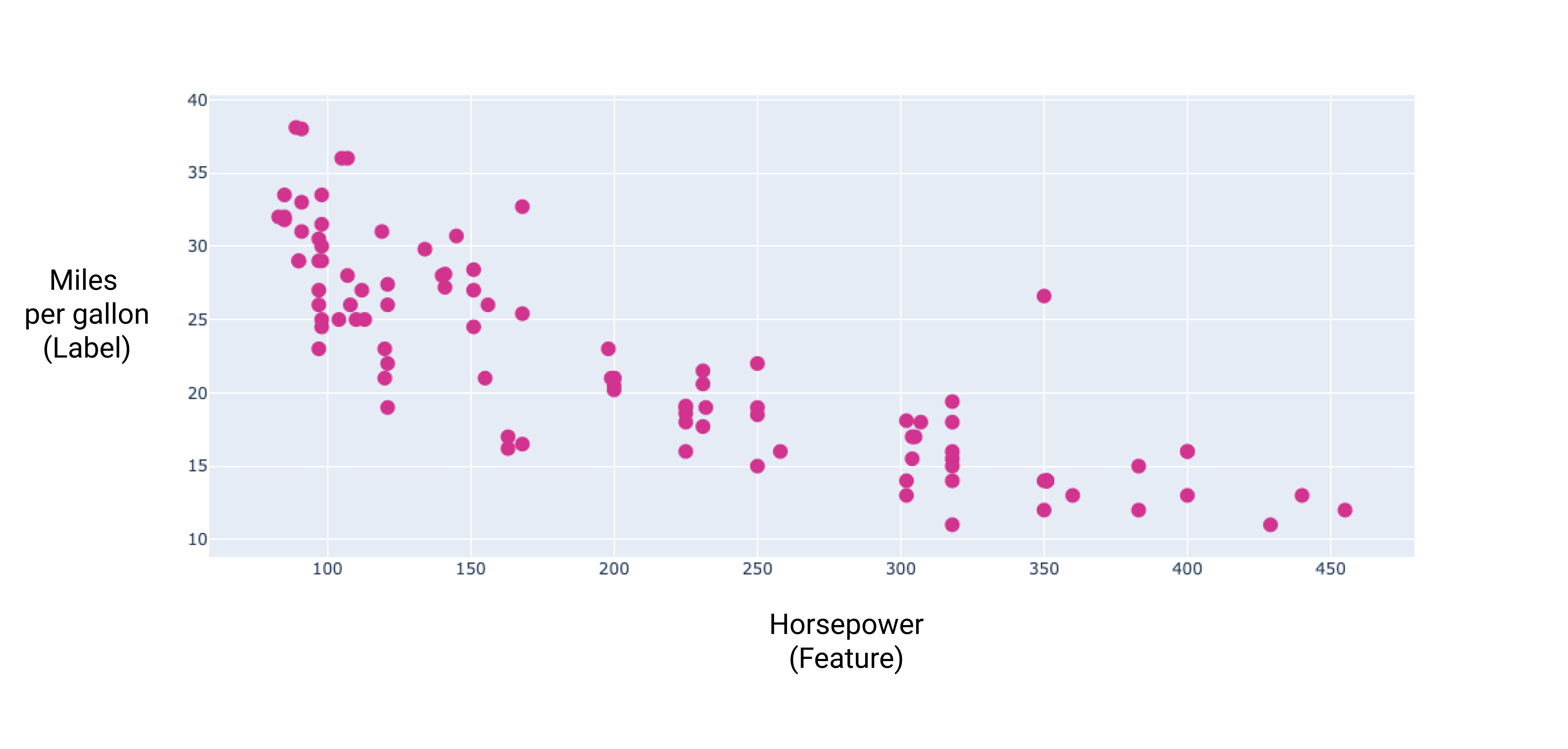
Figura 8. A potência de um carro e a classificação de milhas por litro. Como as informações potência aumenta, a classificação de milhas por galão geralmente diminui.
