このモジュールでは、線形回帰のコンセプトを紹介します。
線形回帰は、変数間の関係を見つけるために使用される統計手法です。ML のコンテキストでは、線形回帰は特徴量とラベルの関係を検出します。
たとえば、車の重量に基づいて車の燃費(ガロンあたりの走行距離)を予測するとします。次のデータセットがあるとします。
| ポンド(1,000 単位)(特徴) | マイル / ガロン (ラベル) |
|---|---|
| 3.5 | 18 |
| 3.69 | 15 |
| 3.44 | 18 |
| 3.43 | 16 |
| 4.34 | 15 |
| 4.42 | 14 |
| 2.37 | 24 |
これらの点をプロットすると、次のグラフが得られます。
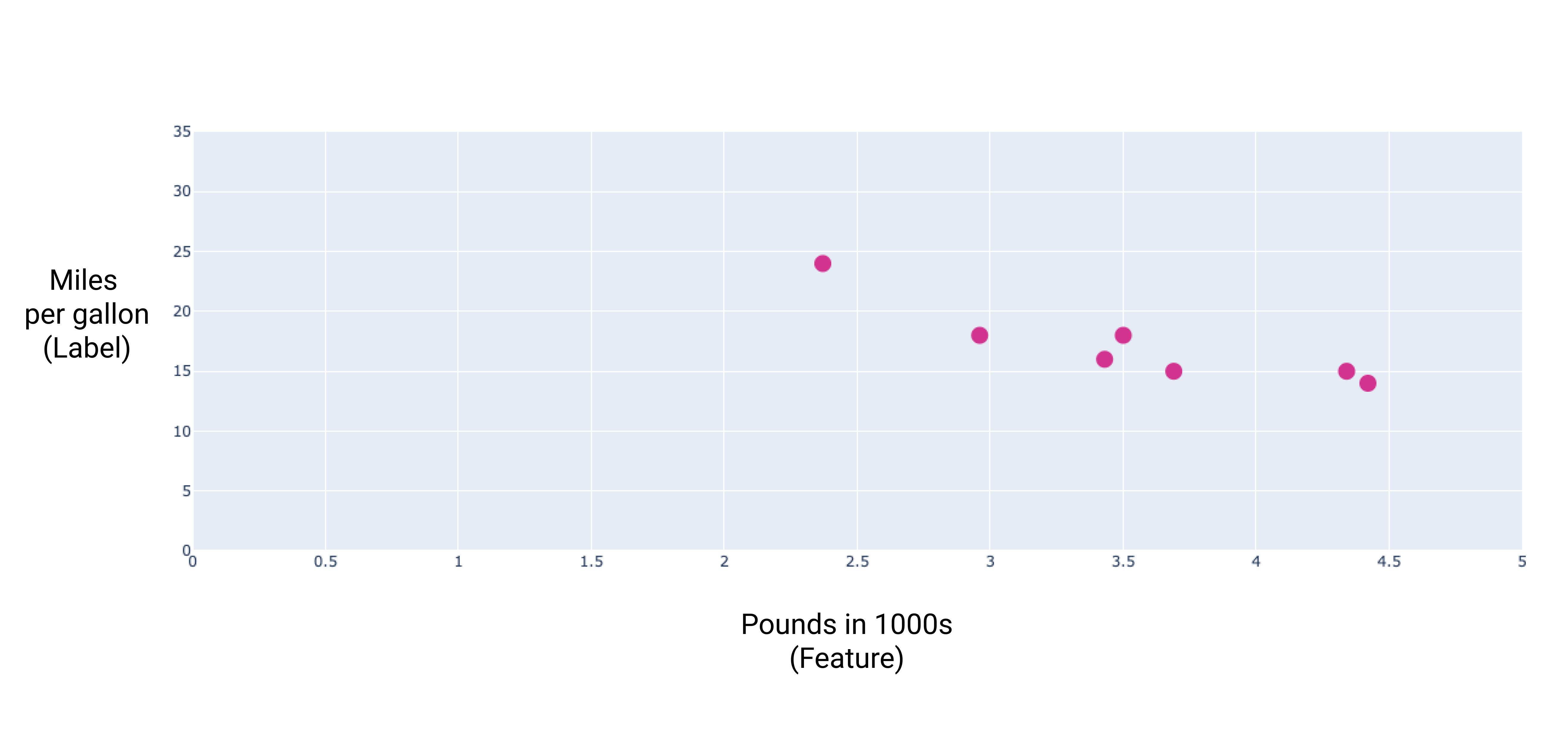
図 1. 自動車の重量(ポンド)と燃費(MPG)の比較。一般的に、車の重量が増すほど、燃費は低下します。
点を結ぶ近似直線を引くことで、独自のモデルを作成できます。
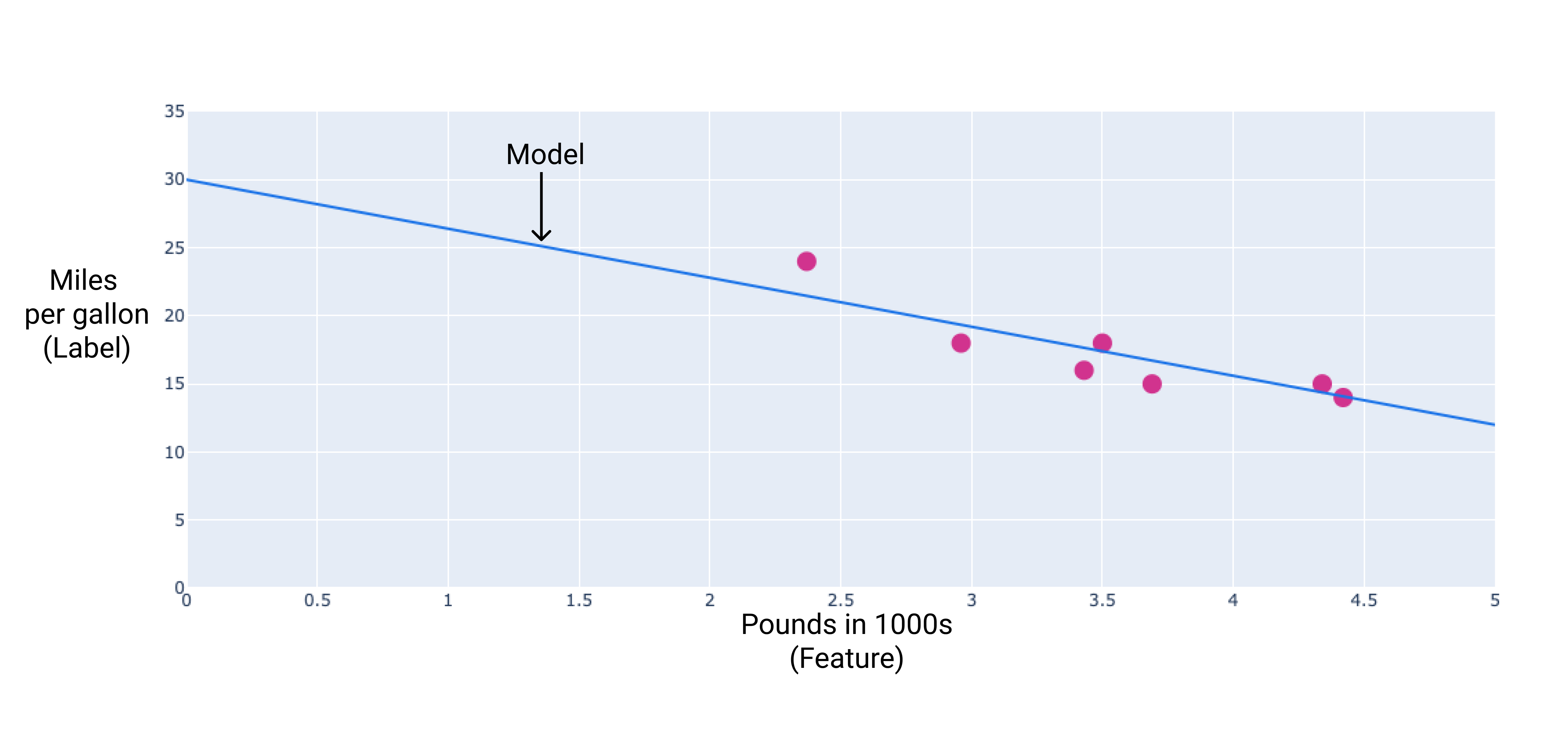
図 2. 前の図のデータを通る近似直線。
線形回帰方程式
代数式で表すと、モデルは $ y = mx + b $ と定義されます。ここで、
- $ y $ はガロンあたりの走行距離(予測する値)です。
- $ m $ は直線の傾きです。
- $ x $ はポンド(入力値)です。
- $ b $ は y 切片です。
ML では、線形回帰モデルの式は次のように記述します。
ここで
- $ y' $ は予測ラベル(出力)です。
- $ b $ はモデルのバイアスです。バイアスは、直線の代数方程式の y 切片と同じ概念です。ML では、バイアスは $ w_0 $ と呼ばれることがあります。バイアスはモデルのパラメータであり、トレーニング中に計算されます。
- $ w_1 $ は特徴の重みです。重みは、直線の代数方程式の傾き $ m $ と同じ概念です。重みはモデルのパラメータであり、トレーニング中に計算されます。
- $ x_1 $ は特徴(入力)です。
トレーニング中に、モデルは最適なモデルを生成する重みとバイアスを計算します。
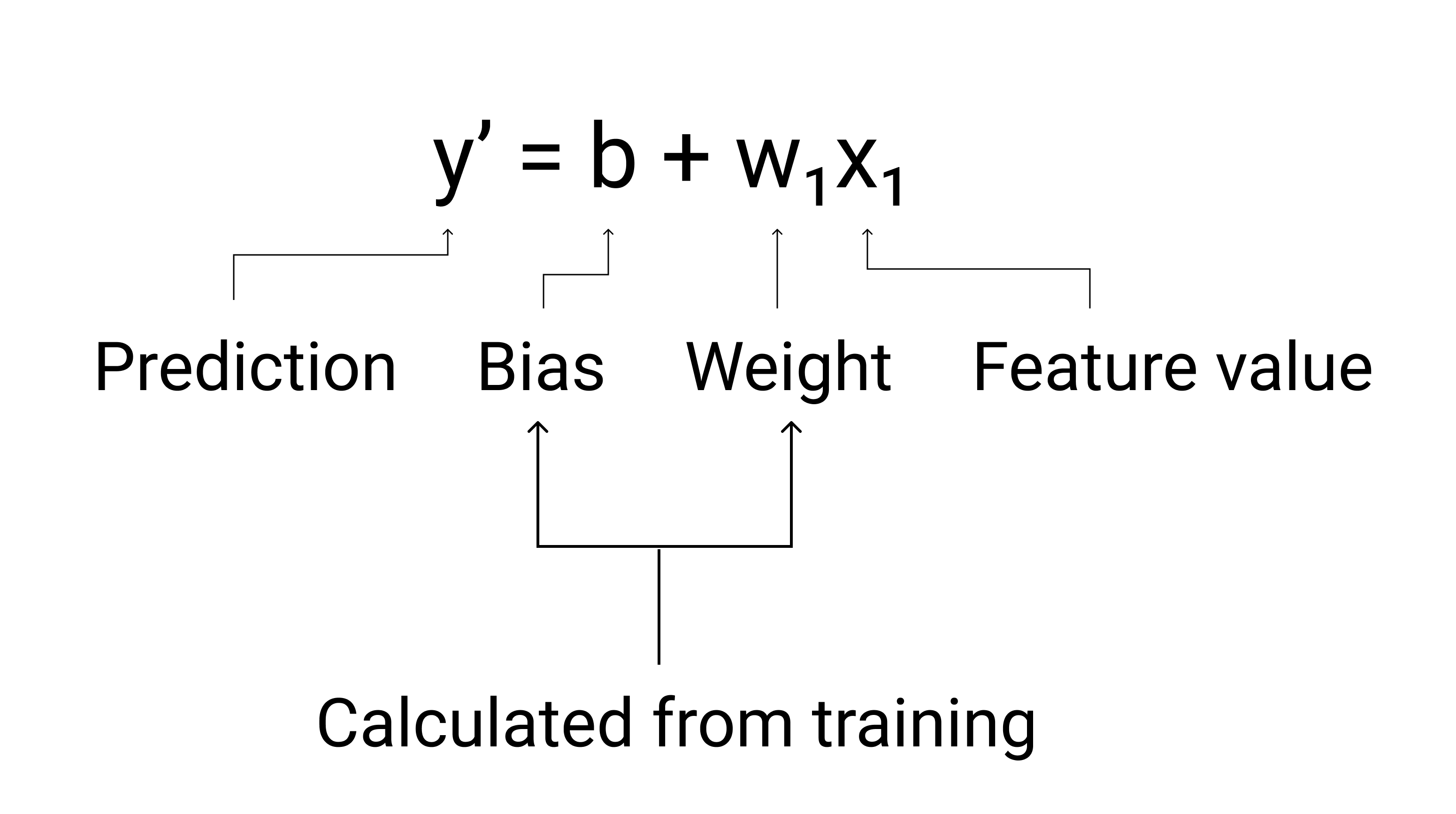
図 3. 線形モデルの数学的表現。
この例では、描画した線から重みとバイアスを計算します。バイアスは 34(線が y 軸と交差する点)、重みは -4.6(線の傾き)です。モデルは $ y' = 34 + (-4.6)(x_1) $ として定義され、これを使用して予測を行うことができます。たとえば、このモデルを使用すると、4,000 ポンドの自動車の燃料効率は 1 ガロンあたり 15.6 マイルと予測されます。
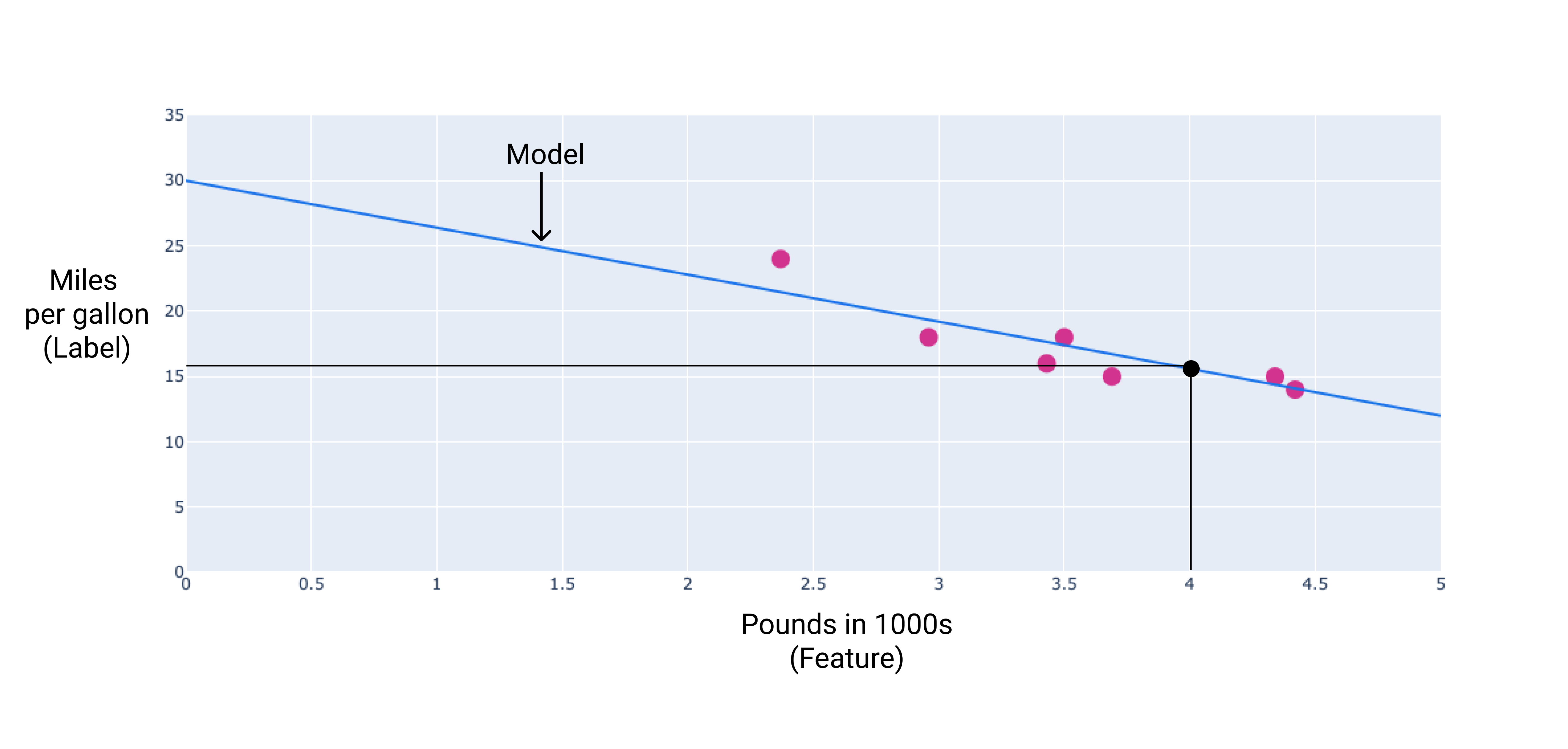
図 4. このモデルを使用すると、4,000 ポンドの自動車の燃費は 1 ガロンあたり 15.6 マイルと予測されます。
複数の特徴量を持つモデル
このセクションの例では、車の重さという 1 つの特徴のみを使用していますが、より高度なモデルでは、それぞれに個別の重み($ w_1 $、$ w_2 $ など)を持つ複数の特徴を使用する場合があります。たとえば、5 つの特徴に依存するモデルは次のように記述します。
$ y' = b + w_1x_1 + w_2x_2 + w_3x_3 + w_4x_4 + w_5x_5 $
たとえば、燃費を予測するモデルでは、次のような特徴をさらに使用できます。
- 排気量
- 加速
- シリンダー数
- 馬力
このモデルは次のように記述します。
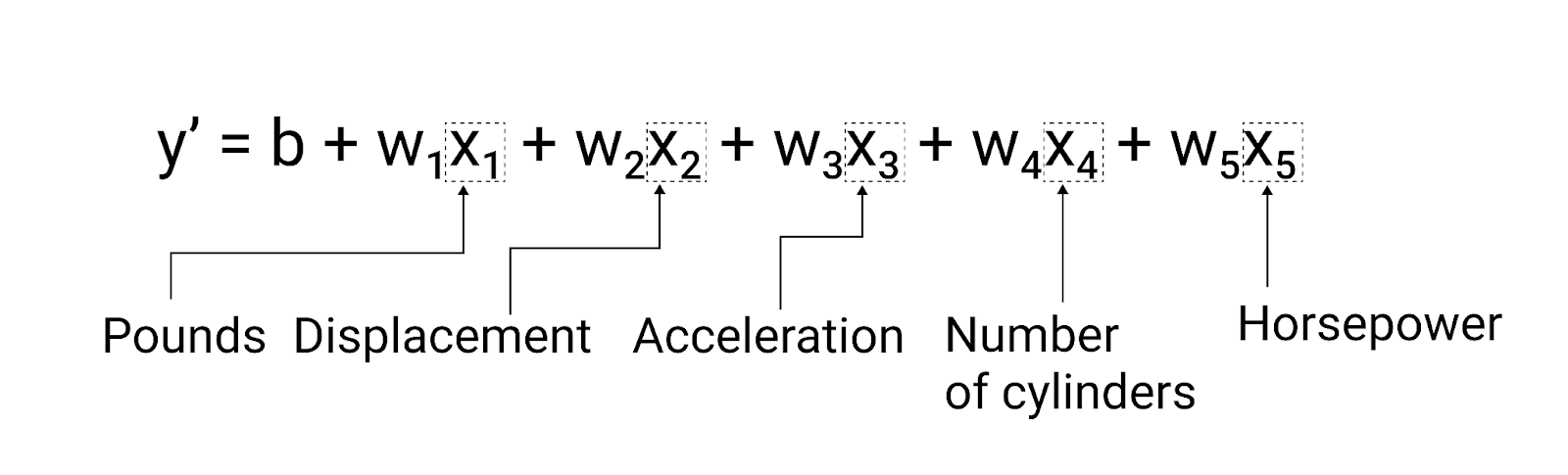
図 5. 自動車の燃費を予測する 5 つの特徴を持つモデル。
これらの追加機能のいくつかについてグラフを作成すると、ラベル(燃費)との間に線形関係があることがわかります。
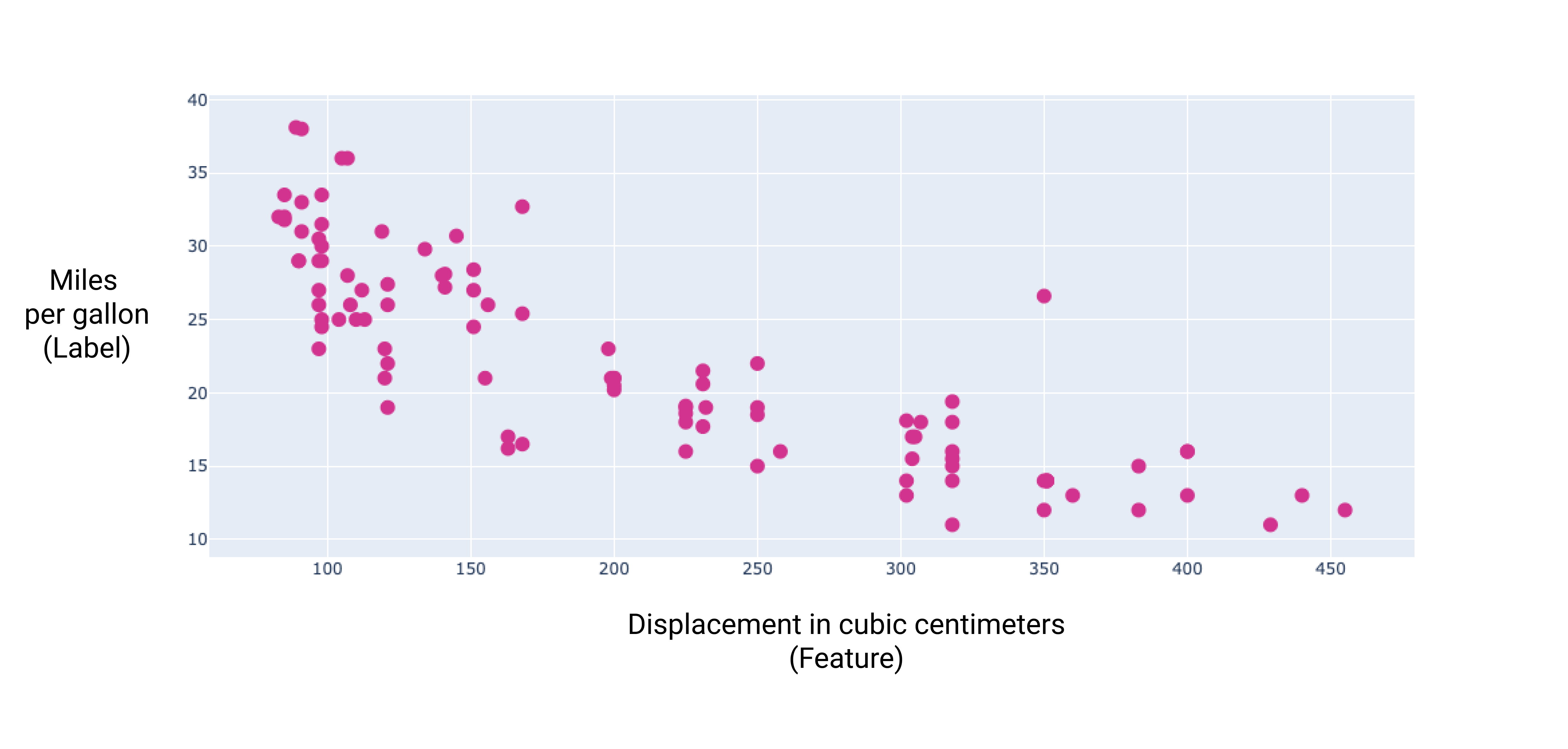
図 6. 自動車の排気量(立方センチメートル)と燃費(マイル / ガロン)。一般的に、自動車のエンジンが大きくなると、燃費は低下します。
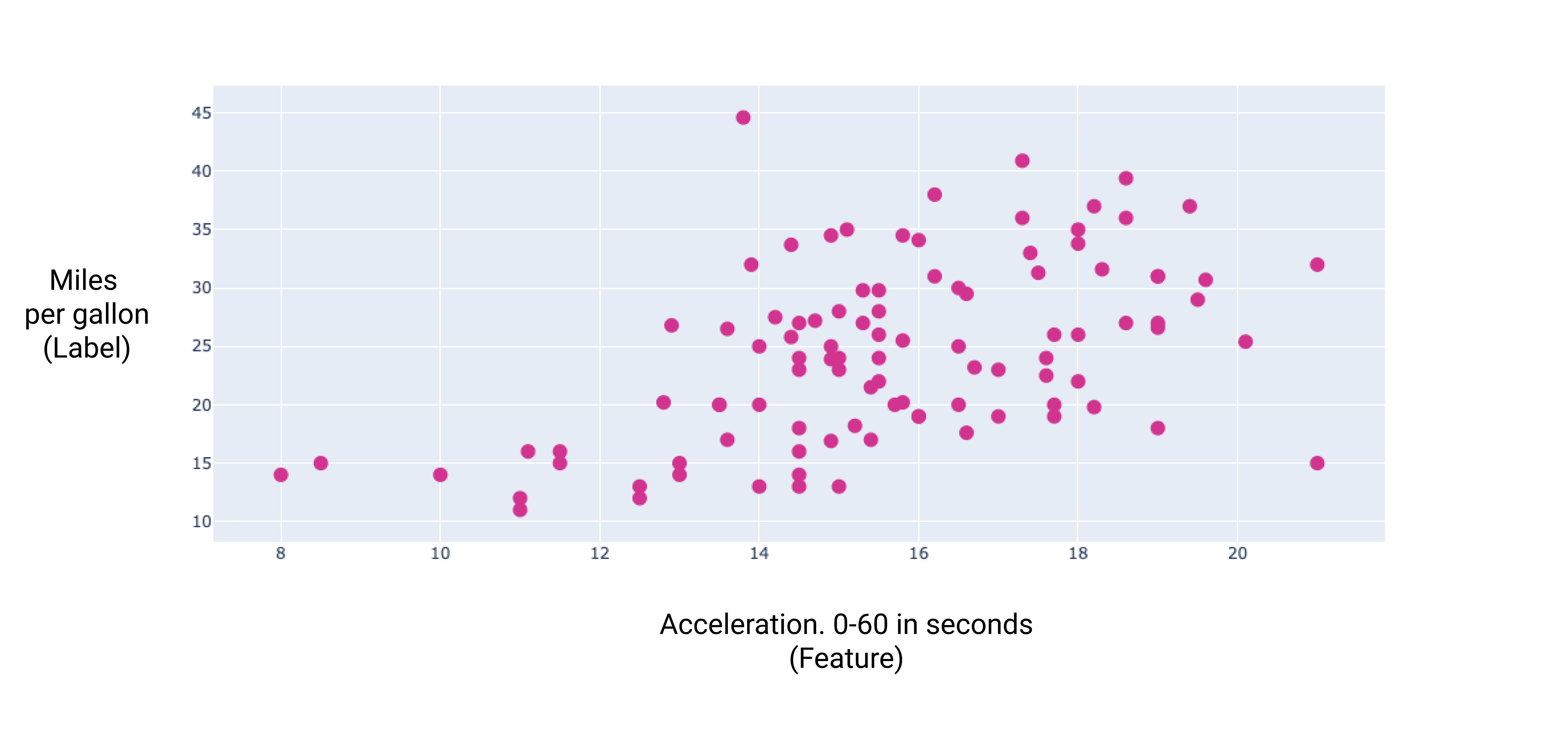
図 7. 車の加速度と燃費。一般的に、車の加速に時間がかかるほど、燃費は向上します。