این ماژول مفاهیم رگرسیون خطی را معرفی میکند.
رگرسیون خطی یک تکنیک آماری است که برای یافتن رابطه بین متغیرها استفاده میشود. در زمینه یادگیری ماشین، رگرسیون خطی رابطه بین ویژگیها و یک برچسب را پیدا میکند.
برای مثال، فرض کنید میخواهیم بر اساس وزن خودرو، میزان مصرف سوخت آن را بر حسب مایل بر گالن پیشبینی کنیم و مجموعه دادههای زیر را داریم:
| پوند در هزار (ویژه) | مایل بر گالن (برچسب) |
|---|---|
| ۳.۵ | ۱۸ |
| ۳.۶۹ | ۱۵ |
| ۳.۴۴ | ۱۸ |
| ۳.۴۳ | ۱۶ |
| ۴.۳۴ | ۱۵ |
| ۴.۴۲ | ۱۴ |
| ۲.۳۷ | ۲۴ |
اگر این نقاط را رسم کنیم، نمودار زیر را خواهیم داشت:

شکل 1. سنگینی خودرو (بر حسب پوند) در مقابل رتبهبندی مایل بر گالن. با سنگینتر شدن خودرو، رتبهبندی مایل بر گالن آن عموماً کاهش مییابد.
ما میتوانیم مدل خودمان را با رسم بهترین خط برازش از میان نقاط ایجاد کنیم:
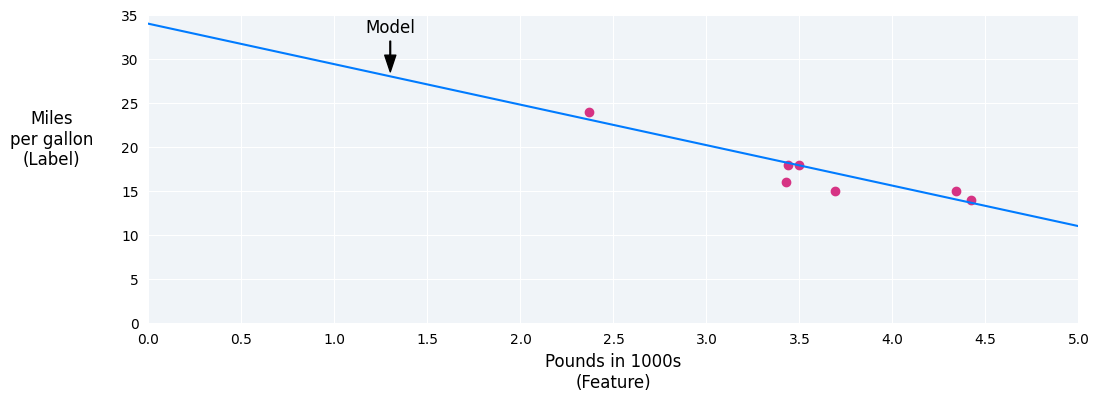
شکل ۲. بهترین خط برازش که از دادههای شکل قبلی عبور داده شده است.
معادله رگرسیون خطی
به زبان جبری، این مدل به صورت $y = mx + b $ تعریف میشود، که در آن
- y$ برابر با مایل بر گالن است - مقداری که میخواهیم پیشبینی کنیم.
- $m $ شیب خط است.
- $x $ برابر با پوند است—مقدار ورودی ما.
- $b $ نقطه تقاطع با y است.
در ML، معادله یک مدل رگرسیون خطی را به صورت زیر مینویسیم:
کجا:
- $y' $ برچسب پیشبینیشده - خروجی - است.
- $b $ بایاس مدل است. بایاس همان مفهوم عرض از مبدا در معادله جبری برای یک خط است. در یادگیری ماشین، بایاس گاهی اوقات به صورت $w_0 $ نامیده میشود. بایاس پارامتری از مدل است و در طول آموزش محاسبه میشود.
- w_1 وزن ویژگی است. وزن همان مفهوم شیب m در معادله جبری برای یک خط را دارد. وزن پارامتری از مدل است و در طول آموزش محاسبه میشود.
- ورودی یک ویژگی است.
در طول آموزش، مدل وزن و بایاس را محاسبه میکند که بهترین مدل را تولید میکند.
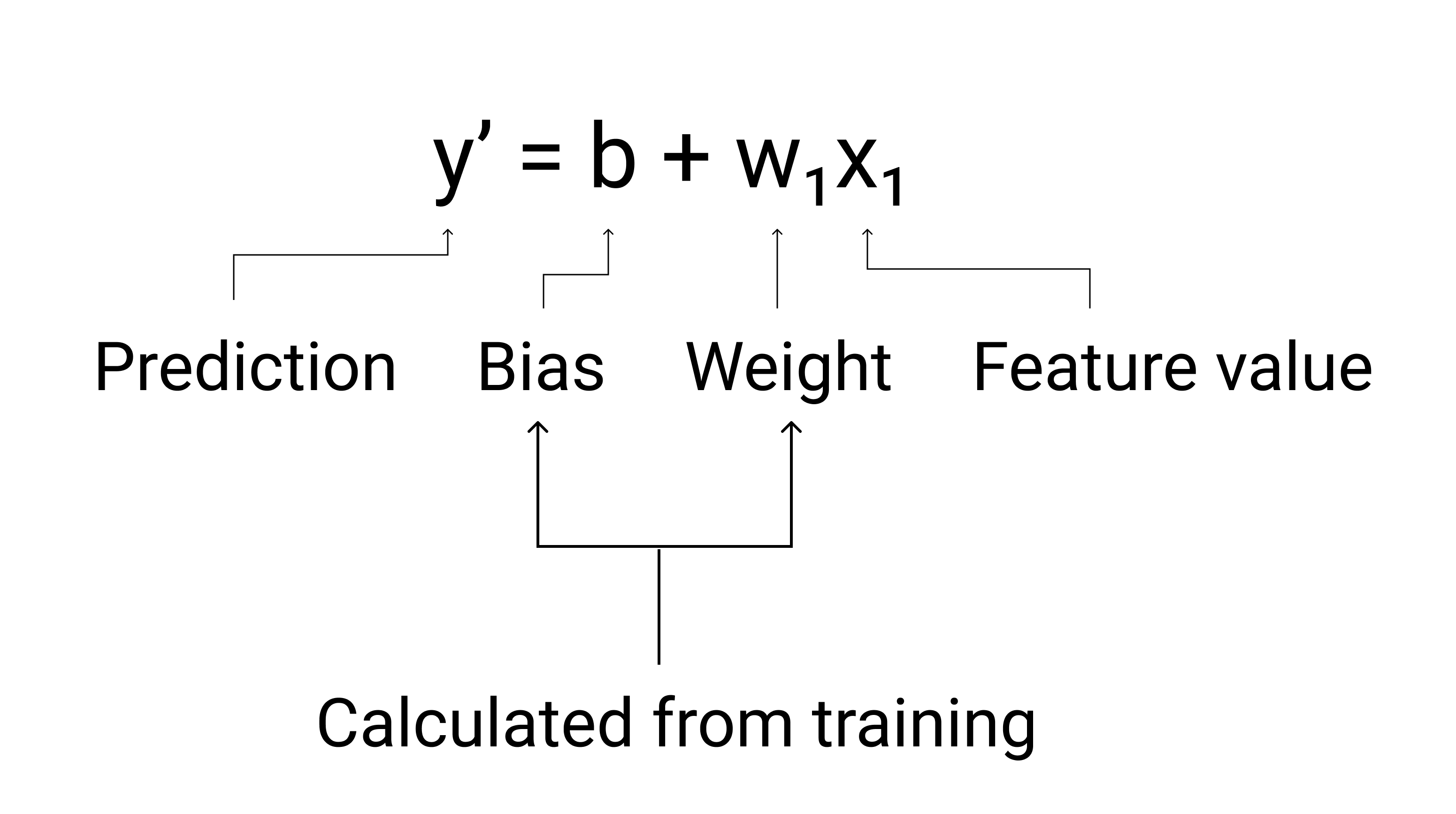
شکل ۳. نمایش ریاضی یک مدل خطی.
در مثال ما، وزن و بایاس را از خطی که رسم کردیم محاسبه میکنیم. بایاس ۳۴ است (جایی که خط محور y را قطع میکند) و وزن -۴.۶ است (شیب خط). این مدل به صورت $y' = 34 + (-4.6)(x_1) $ تعریف میشود و میتوانیم از آن برای پیشبینی استفاده کنیم. به عنوان مثال، با استفاده از این مدل، یک ماشین ۴۰۰۰ پوندی، راندمان سوخت پیشبینیشده ۱۵.۶ مایل در هر گالن خواهد داشت.

شکل ۴. با استفاده از مدل، یک خودروی ۴۰۰۰ پوندی، راندمان سوخت پیشبینیشده ۱۵.۶ مایل در هر گالن دارد.
مدلهایی با ویژگیهای متعدد
اگرچه مثال این بخش فقط از یک ویژگی - سنگینی ماشین - استفاده میکند، اما یک مدل پیچیدهتر ممکن است به چندین ویژگی متکی باشد که هر کدام وزن جداگانهای دارند ($ w_1 $، $ w_2 $ و غیره). برای مثال، مدلی که به پنج ویژگی متکی است به صورت زیر نوشته میشود:
$ y' = b + w_1x_1 + w_2x_2 + w_3x_3 + w_4x_4 + w_5x_5 دلار
برای مثال، مدلی که میزان مصرف سوخت را پیشبینی میکند، میتواند از ویژگیهای دیگری مانند موارد زیر نیز استفاده کند:
- حجم موتور
- شتاب
- تعداد سیلندرها
- اسب بخار
این مدل به صورت زیر نوشته خواهد شد:
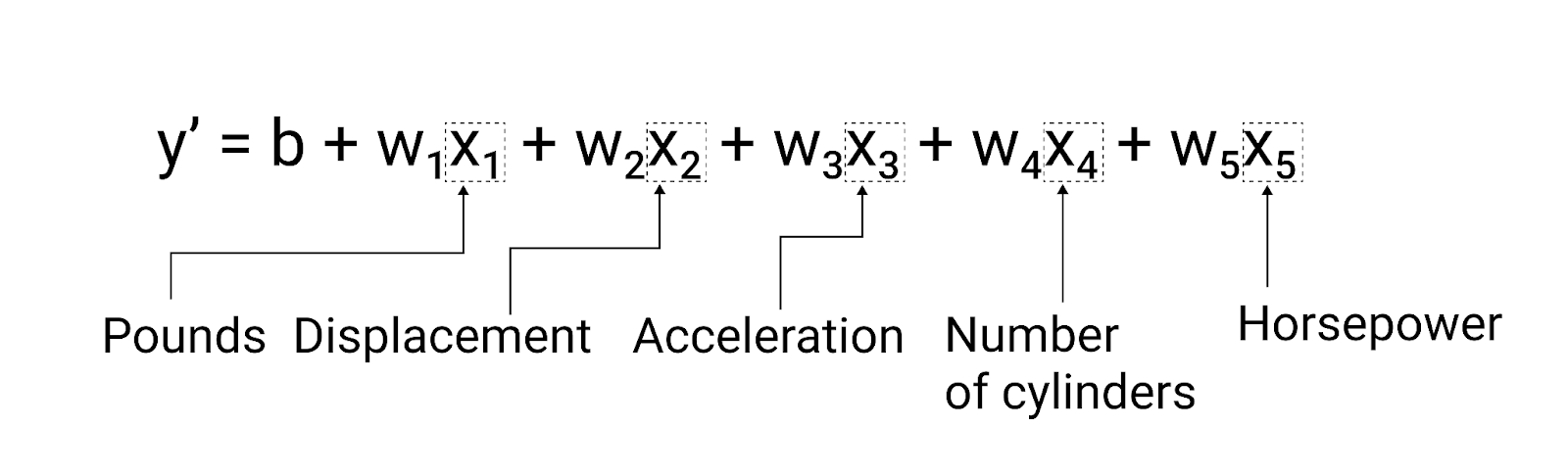
شکل ۵. مدلی با پنج ویژگی برای پیشبینی میزان مصرف سوخت خودرو بر حسب مایل در هر گالن.
با رسم نمودار چند مورد از این ویژگیهای اضافی، میتوانیم ببینیم که آنها نیز رابطهای خطی با برچسب، مایل بر گالن، دارند:

شکل 6. حجم موتور خودرو بر حسب سانتیمتر مکعب و میزان مصرف سوخت آن (مایل بر گالن). با بزرگتر شدن موتور خودرو، میزان مصرف سوخت آن (مایل بر گالن) عموماً کاهش مییابد.

شکل 7. شتاب خودرو و میزان مصرف سوخت آن (مایل بر گالن). هرچه شتاب خودرو بیشتر طول بکشد، میزان مصرف سوخت آن (مایل بر گالن) عموماً افزایش مییابد.
