Este módulo apresenta os conceitos de regressão linear.
A regressão linear é uma técnica estatística usada para encontrar a relação entre variáveis. Em um contexto de ML, a regressão linear encontra a relação entre atributos e um rótulo.
Por exemplo, suponha que queremos prever a eficiência de combustível de um carro em milhas por galão com base no peso do veículo e temos o seguinte conjunto de dados:
| Libras em milhares (recurso) | Milhas por galão (rótulo) |
|---|---|
| 3.5 | 18 |
| 3,69 | 15 |
| 3,44 | 18 |
| 3,43 | 16 |
| 4,34 | 15 |
| 4,42 | 14 |
| 2,37 | 24 |
Se representarmos esses pontos, vamos ter o seguinte gráfico:
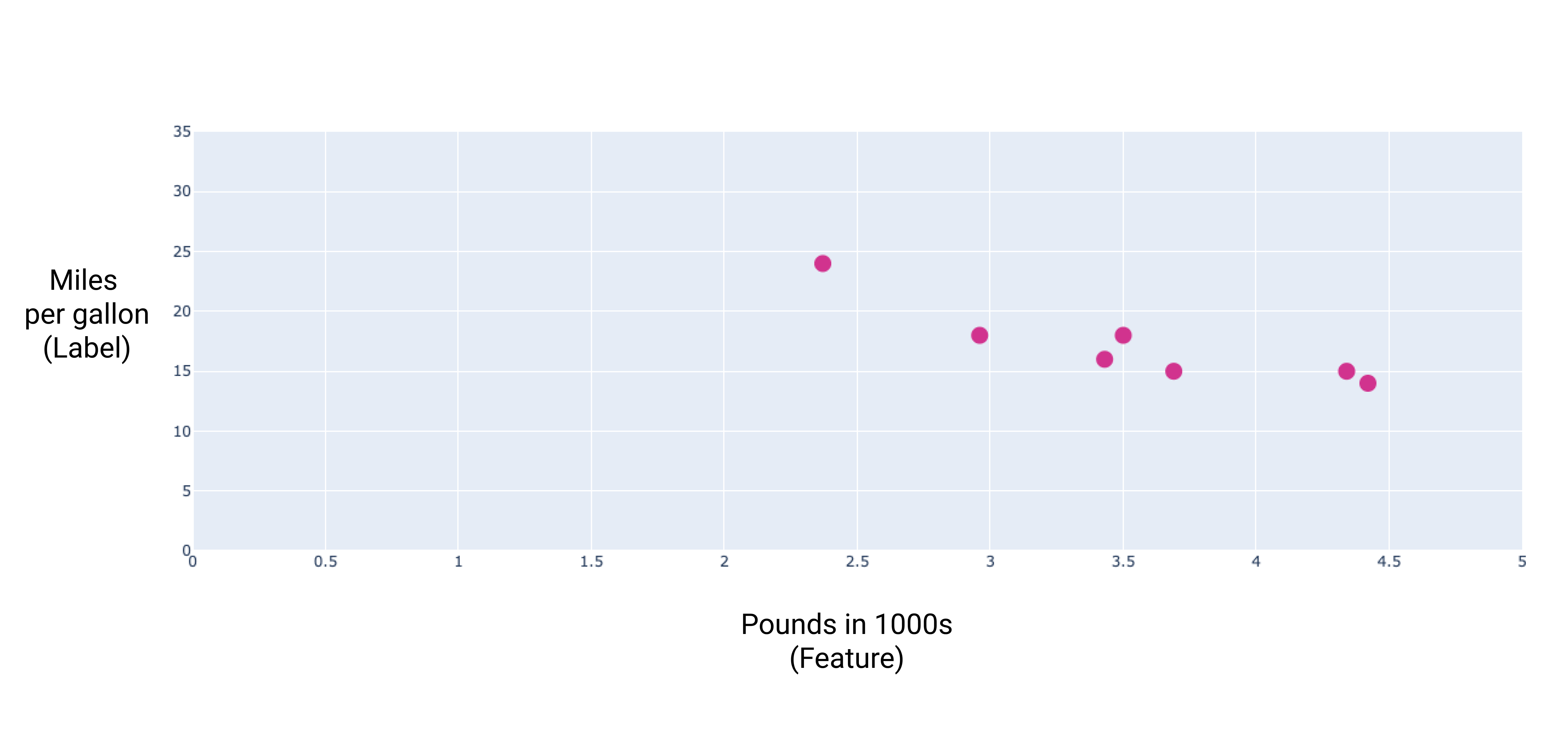
Figura 1. Peso do carro (em libras) x classificação de milhas por galão. À medida que um carro fica mais pesado, a classificação de quilômetros por galão geralmente diminui.
Podemos criar nosso próprio modelo desenhando uma reta de regressão pelos pontos:
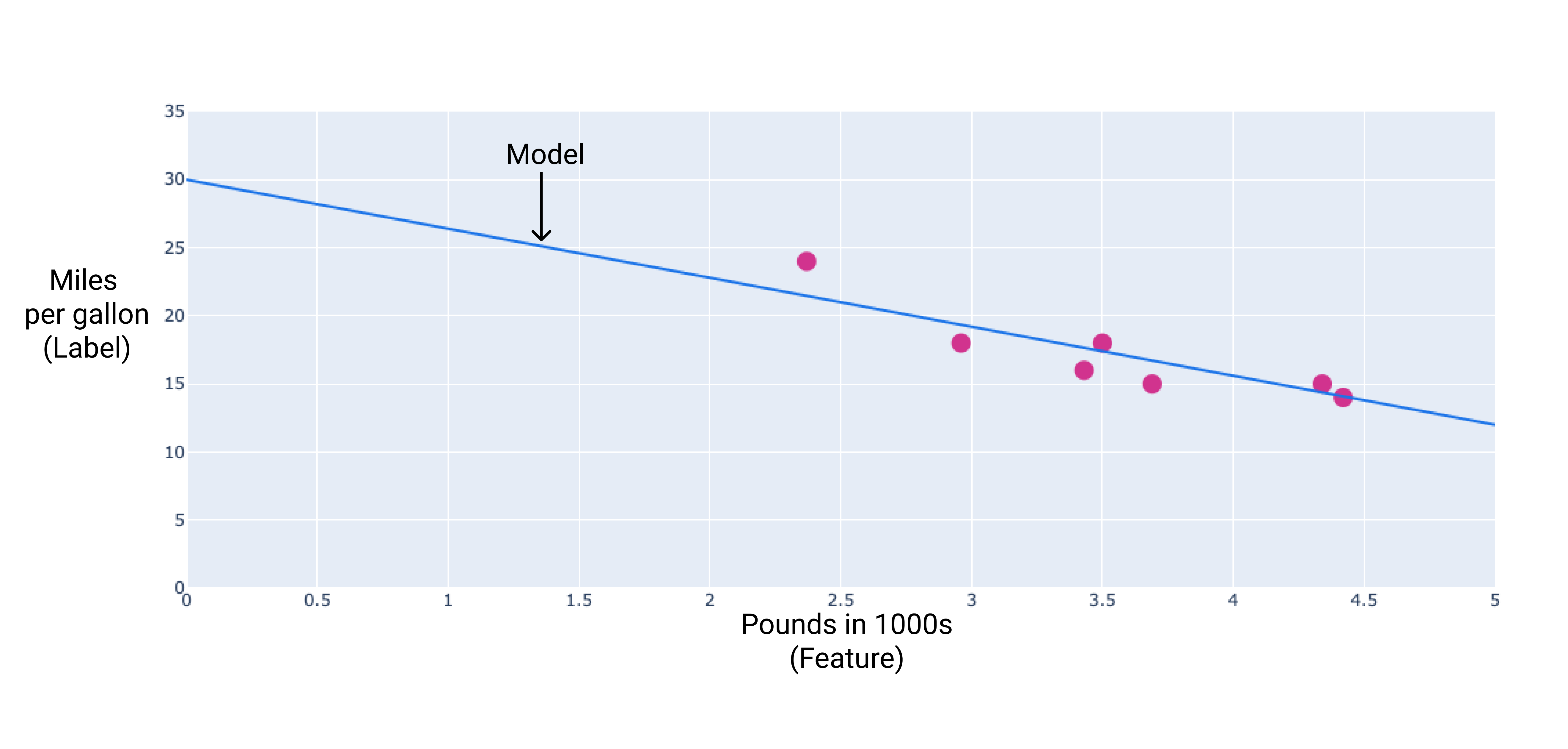
Figura 2. Uma reta de regressão traçada pelos dados da figura anterior.
Equação de regressão linear
Em termos algébricos, o modelo seria definido como $ y = mx + b $, em que
- $ y $ é milhas por galão, o valor que queremos prever.
- $ m $ é a inclinação da linha.
- $ x $ é libras, nosso valor de entrada.
- $ b $ é a interseção y.
Em ML, escrevemos a equação para um modelo de regressão linear da seguinte maneira:
em que:
- $ y' $ é o rótulo previsto, ou seja, a saída.
- $ b $ é o viés do modelo. O viés é o mesmo conceito da interceptação y na equação algébrica de uma reta. Em ML, o viés às vezes é chamado de $ w_0 $. O viés é um parâmetro do modelo e é calculado durante o treinamento.
- $ w_1 $ é o peso do recurso. O peso é o mesmo conceito da inclinação $ m $ na equação algébrica de uma reta. O peso é um parâmetro do modelo e é calculado durante o treinamento.
- $ x_1 $ é um atributo, ou seja, a entrada.
Durante o treinamento, o modelo calcula o peso e o viés que produzem o melhor modelo.
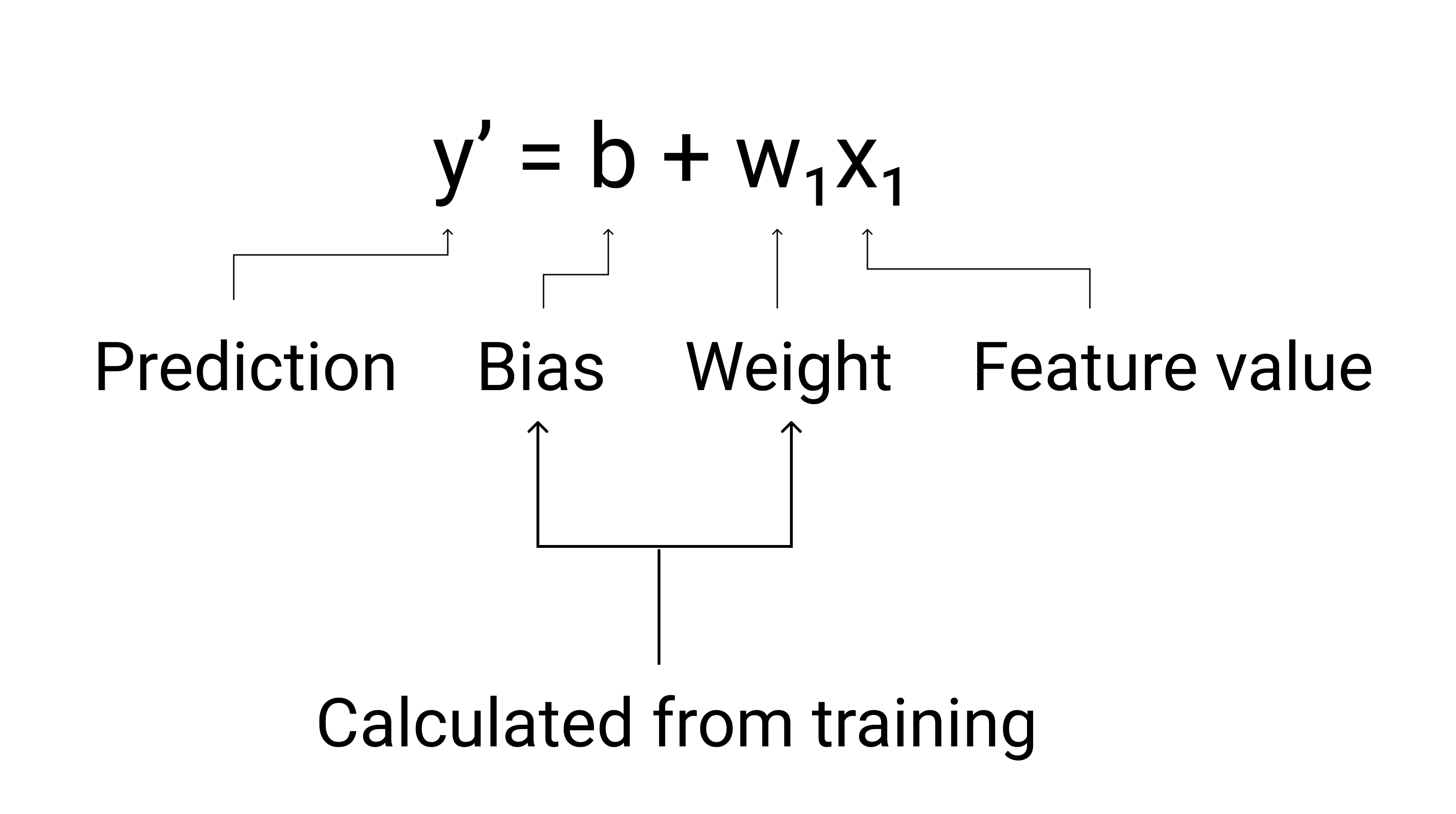
Figura 3. Representação matemática de um modelo linear.
No nosso exemplo, calcularíamos o peso e o viés da linha que desenhamos. O viés é 34 (onde a linha cruza o eixo y), e a ponderação é -4,6 (a inclinação da linha). O modelo seria definido como $ y' = 34 + (-4.6)(x_1) $, e poderíamos usá-lo para fazer previsões. Por exemplo, usando esse modelo, um carro de 1.800 kg teria uma eficiência de combustível prevista de 6,6 km por litro.
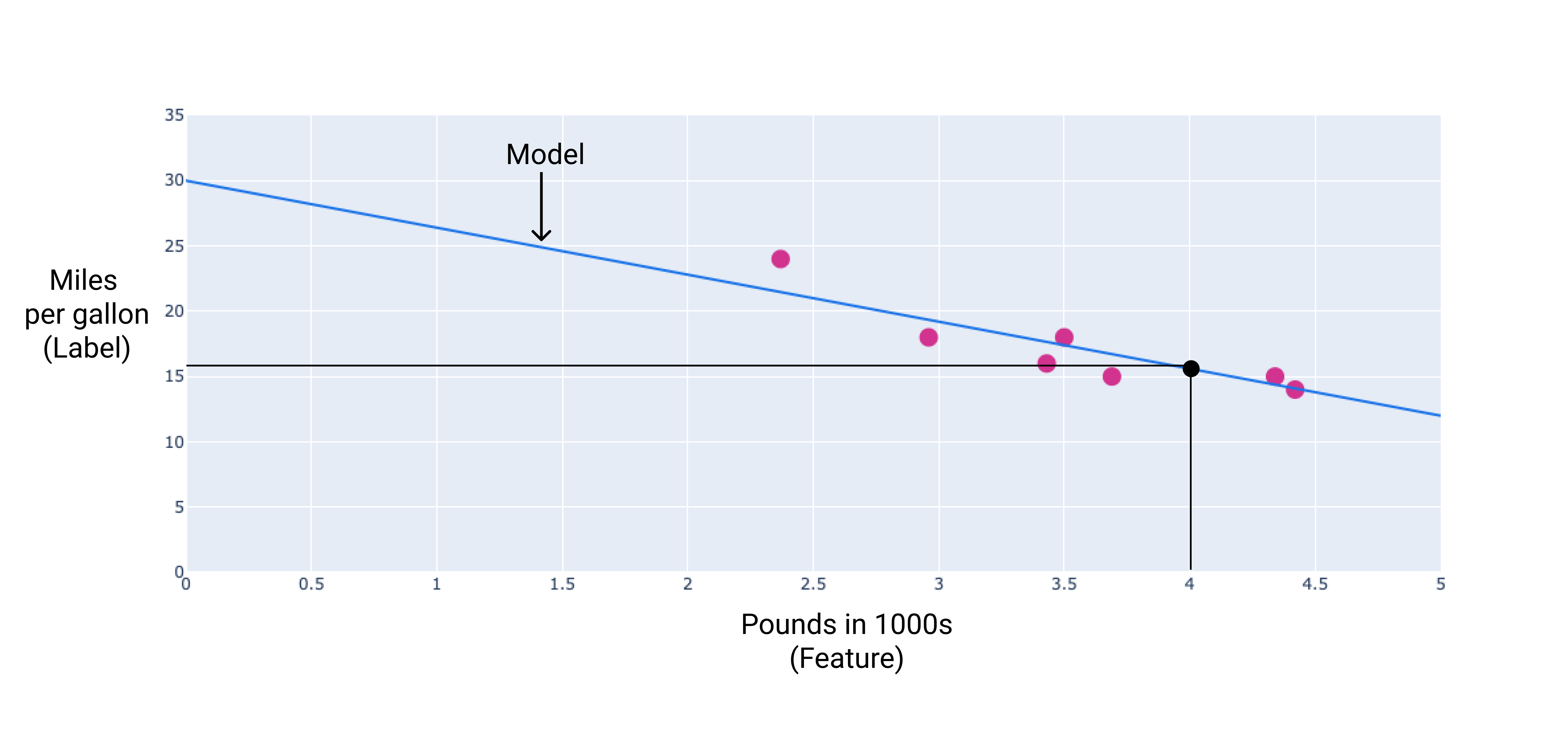
Figura 4. Usando o modelo, um carro de 1.800 kg tem uma eficiência de combustível prevista de 6,6 quilômetros por litro.
Modelos com vários recursos
Embora o exemplo nesta seção use apenas um recurso (o peso do carro), um modelo mais sofisticado pode depender de vários recursos, cada um com um peso separado ($ w_1 $, $ w_2 $ etc.). Por exemplo, um modelo que depende de cinco recursos seria escrito da seguinte forma:
$ y' = b + w_1x_1 + w_2x_2 + w_3x_3 + w_4x_4 + w_5x_5 $
Por exemplo, um modelo que prevê a quilometragem por litro de gasolina também pode usar recursos como:
- Cilindrada do motor
- Aceleração
- Número de cilindros
- Cavalos de potência
Esse modelo seria escrito da seguinte forma:
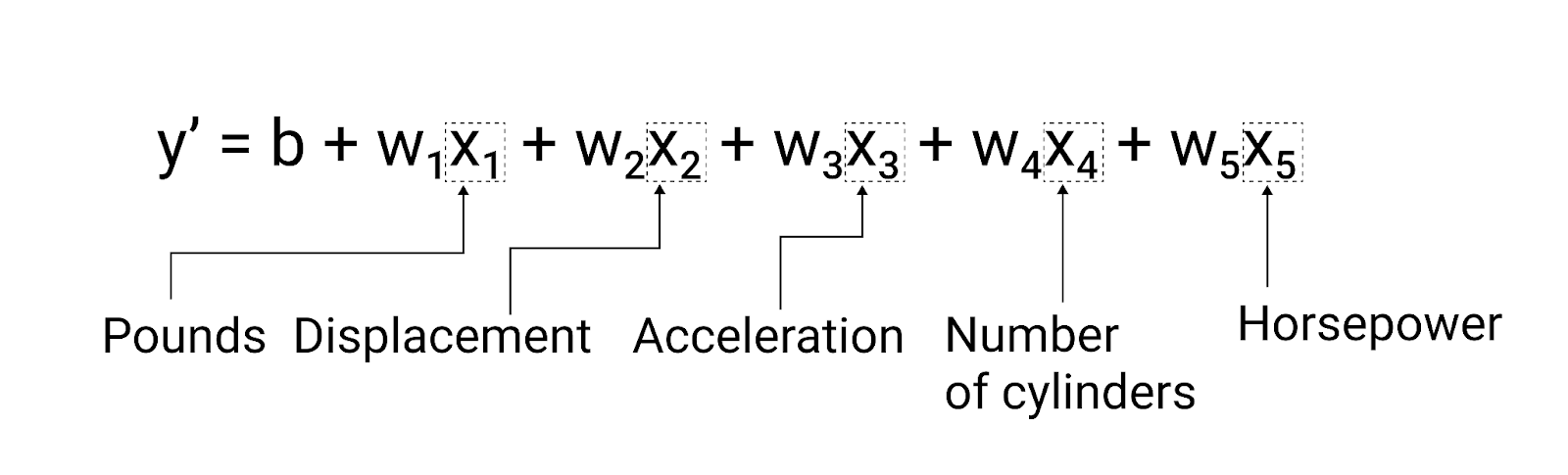
Figura 5. Um modelo com cinco recursos para prever a classificação de milhas por galão de um carro.
Ao representar graficamente alguns desses recursos adicionais, podemos ver que eles também têm uma relação linear com o rótulo, milhas por galão:
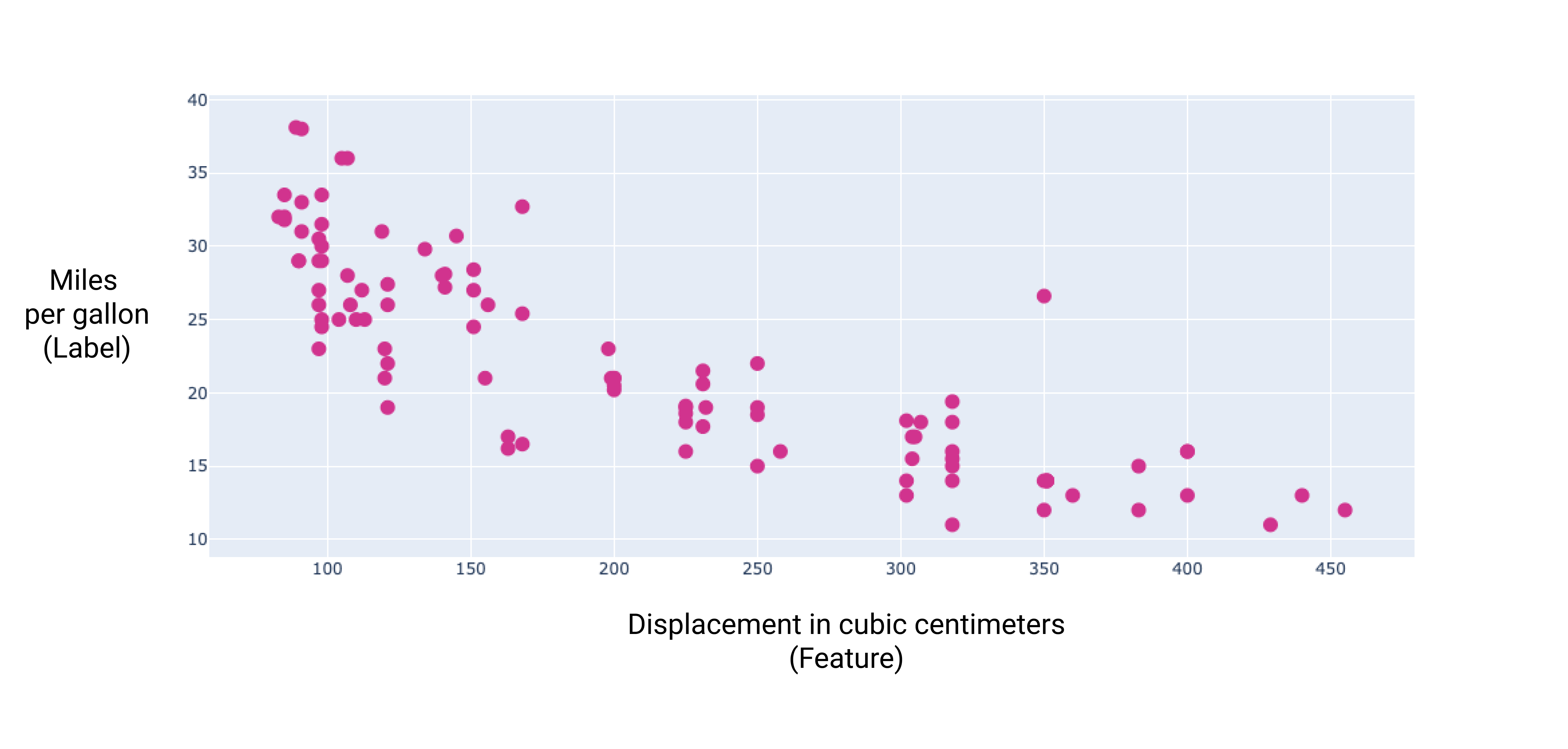
Figura 6. O deslocamento de um carro em centímetros cúbicos e sua classificação de milhas por galão. À medida que o motor de um carro aumenta, a classificação de milhas por galão geralmente diminui.
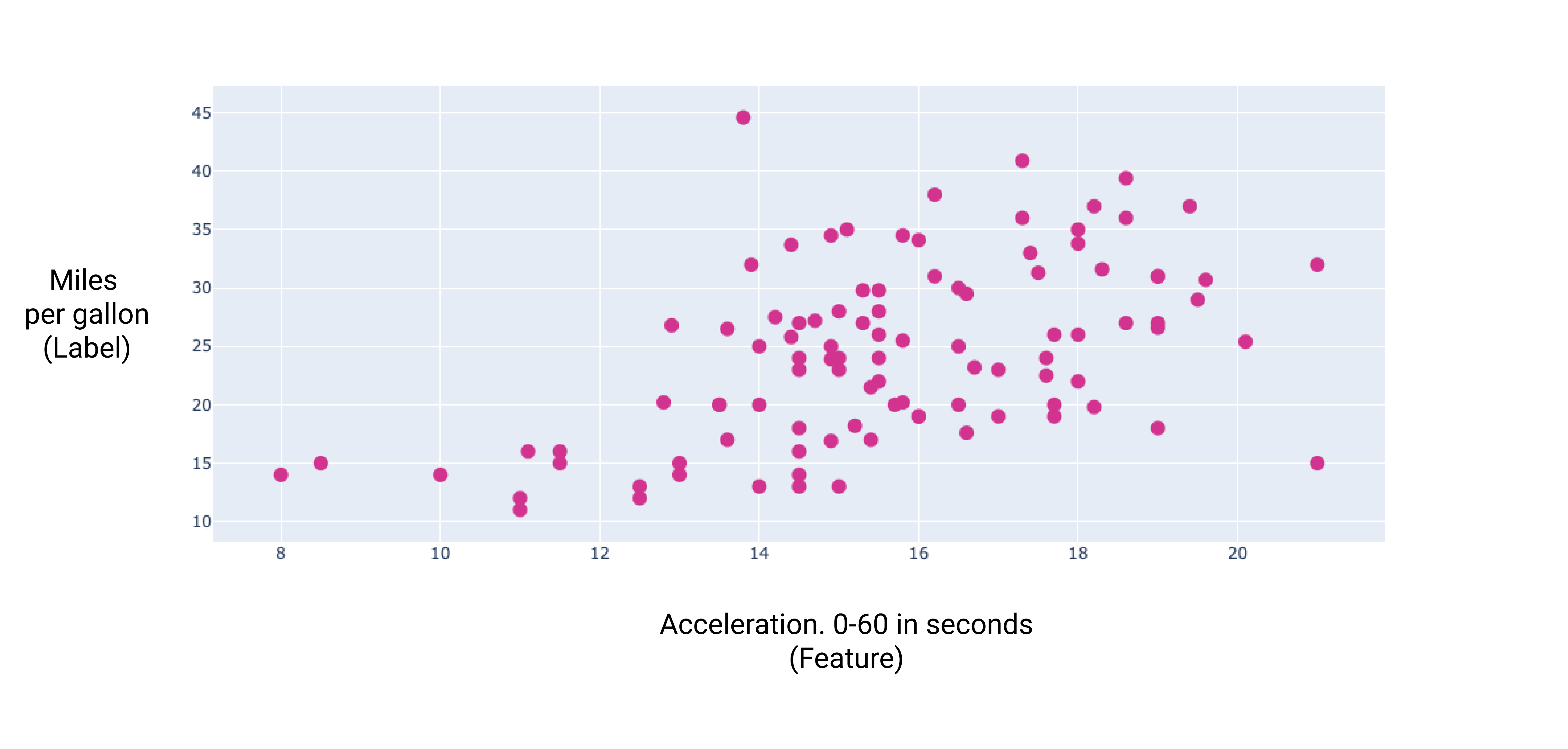
Figura 7. A aceleração de um carro e a classificação de milhas por galão. Quanto mais tempo leva a aceleração de um carro, maior é a classificação de quilômetros por galão.