Mô-đun này giới thiệu các khái niệm về hồi quy tuyến tính.
Hồi quy tuyến tính là một kỹ thuật thống kê được dùng để tìm mối quan hệ giữa các biến. Trong bối cảnh học máy, hồi quy tuyến tính tìm ra mối quan hệ giữa các đặc điểm và một nhãn.
Ví dụ: giả sử chúng ta muốn dự đoán mức tiêu thụ nhiên liệu của một chiếc ô tô theo số dặm trên một gallon dựa trên trọng lượng của chiếc ô tô đó và chúng ta có tập dữ liệu sau:
| Pao (tính bằng nghìn) (đối tượng) | Số dặm trên mỗi ga lông (nhãn) |
|---|---|
| 3,5 | 18 |
| 3,69 | 15 |
| 3,44 | 18 |
| 3,43 | 16 |
| 4,34 | 15 |
| 4,42 | 14 |
| 2,37 | 24 |
Nếu vẽ các điểm này, chúng ta sẽ có biểu đồ sau:
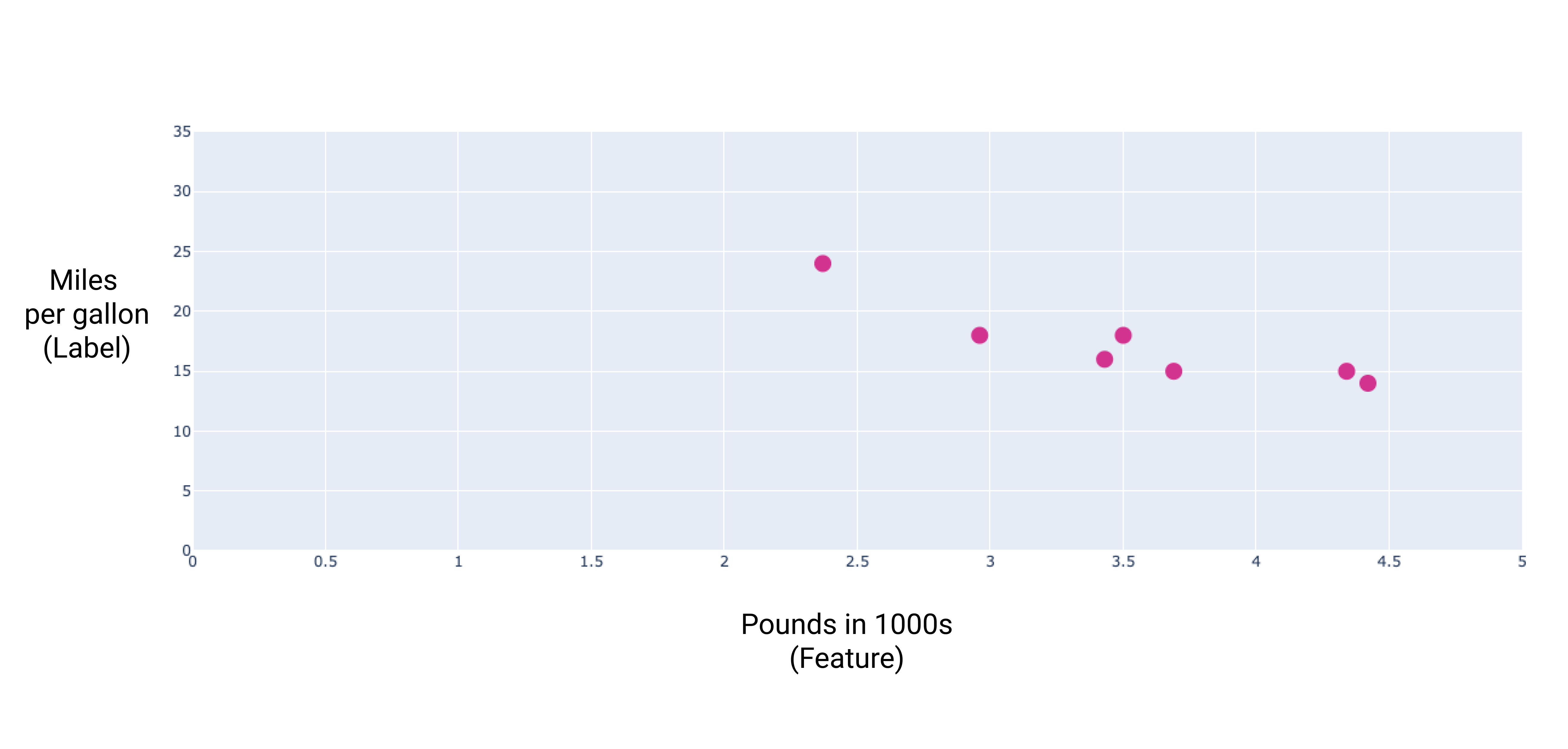
Hình 1 Trọng lượng của xe (tính bằng pound) so với mức tiêu thụ nhiên liệu (tính bằng dặm trên mỗi gallon). Khi ô tô càng nặng, chỉ số quãng đường đi được trên một gallon nhiên liệu thường giảm.
Chúng ta có thể tạo mô hình riêng bằng cách vẽ một đường phù hợp nhất qua các điểm:
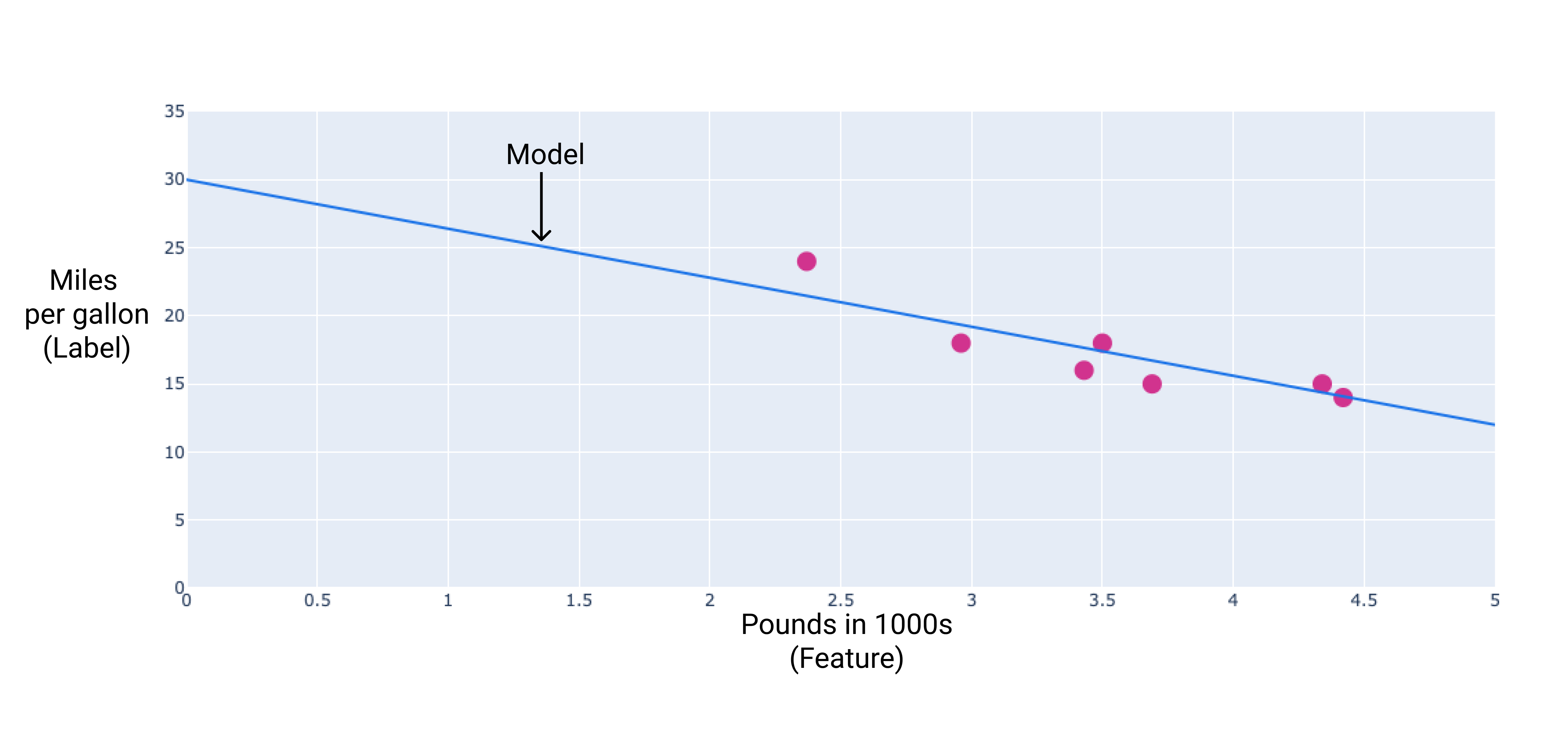
Hình 2. Đường phù hợp nhất được vẽ qua dữ liệu trong hình trước.
Phương trình hồi quy tuyến tính
Về mặt đại số, mô hình sẽ được xác định là $ y = mx + b $, trong đó
- $ y $ là số dặm trên một gallon – giá trị mà chúng ta muốn dự đoán.
- $ m $ là hệ số góc của đường thẳng.
- $ x $ là đơn vị pound – giá trị đầu vào của chúng ta.
- $ b $ là tung độ gốc.
Trong học máy, chúng ta viết phương trình cho mô hình hồi quy tuyến tính như sau:
trong đó:
- $ y' $ là nhãn được dự đoán – đầu ra.
- $ b $ là độ chênh lệch của mô hình. Độ lệch cũng là khái niệm tương tự như tung độ gốc trong phương trình đại số của một đường thẳng. Trong học máy, độ chênh lệch đôi khi được gọi là $ w_0 $. Độ chênh lệch là một tham số của mô hình và được tính trong quá trình huấn luyện.
- $ w_1 $ là trọng số của đối tượng. Trọng số cũng là khái niệm tương tự như độ dốc $ m $ trong phương trình đại số của một đường thẳng. Trọng số là một tham số của mô hình và được tính toán trong quá trình huấn luyện.
- $ x_1 $ là một đặc điểm – dữ liệu đầu vào.
Trong quá trình huấn luyện, mô hình sẽ tính toán trọng số và độ lệch tạo ra mô hình tốt nhất.
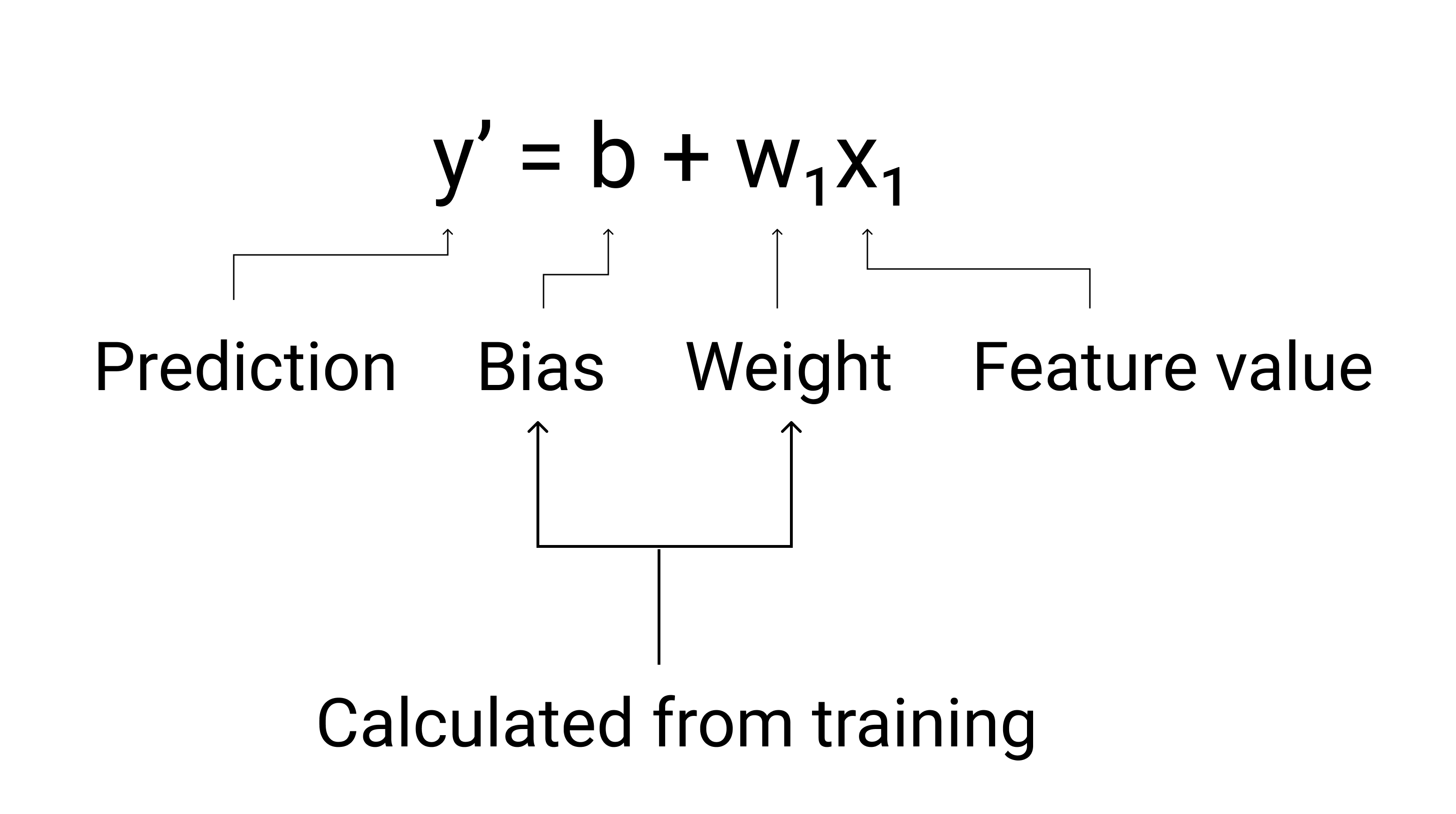
Hình 3. Biểu diễn toán học của một mô hình tuyến tính.
Trong ví dụ này, chúng ta sẽ tính toán trọng số và độ lệch từ đường thẳng mà chúng ta đã vẽ. Độ lệch là 34 (nơi đường thẳng cắt trục y) và trọng số là –4,6 (độ dốc của đường thẳng). Mô hình sẽ được xác định là $ y' = 34 + (-4.6)(x_1) $ và chúng ta có thể sử dụng mô hình này để dự đoán. Ví dụ: khi sử dụng mô hình này, một chiếc ô tô nặng 4.000 pound sẽ có mức tiêu thụ nhiên liệu dự đoán là 15,6 dặm/gallon.
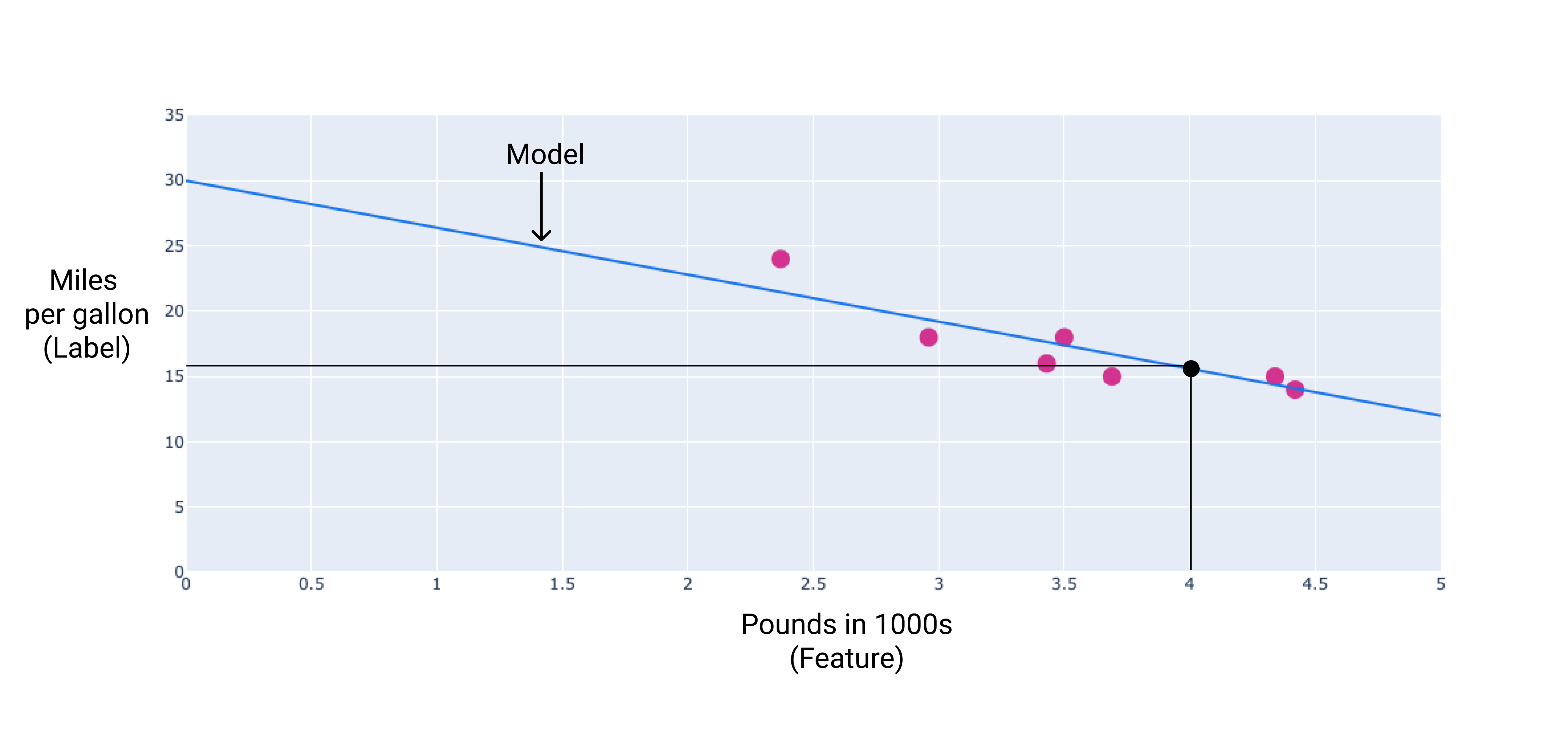
Hình 4. Theo mô hình này, một chiếc xe nặng 4.000 pound có hiệu suất sử dụng nhiên liệu dự kiến là 15,6 dặm/gallon.
Mô hình có nhiều tính năng
Mặc dù ví dụ trong phần này chỉ sử dụng một đặc điểm (độ nặng của ô tô), nhưng một mô hình phức tạp hơn có thể dựa vào nhiều đặc điểm, mỗi đặc điểm có một trọng số riêng ($ w_1 $, $ w_2 $, v.v.). Ví dụ: một mô hình dựa trên 5 đặc điểm sẽ được viết như sau:
$ y' = b + w_1x_1 + w_2x_2 + w_3x_3 + w_4x_4 + w_5x_5 $
Ví dụ: một mô hình dự đoán mức tiêu thụ nhiên liệu có thể sử dụng thêm các đặc điểm như sau:
- Dung tích động cơ
- Tăng tốc
- Số lượng xi-lanh
- Mã lực
Mô hình này sẽ được viết như sau:
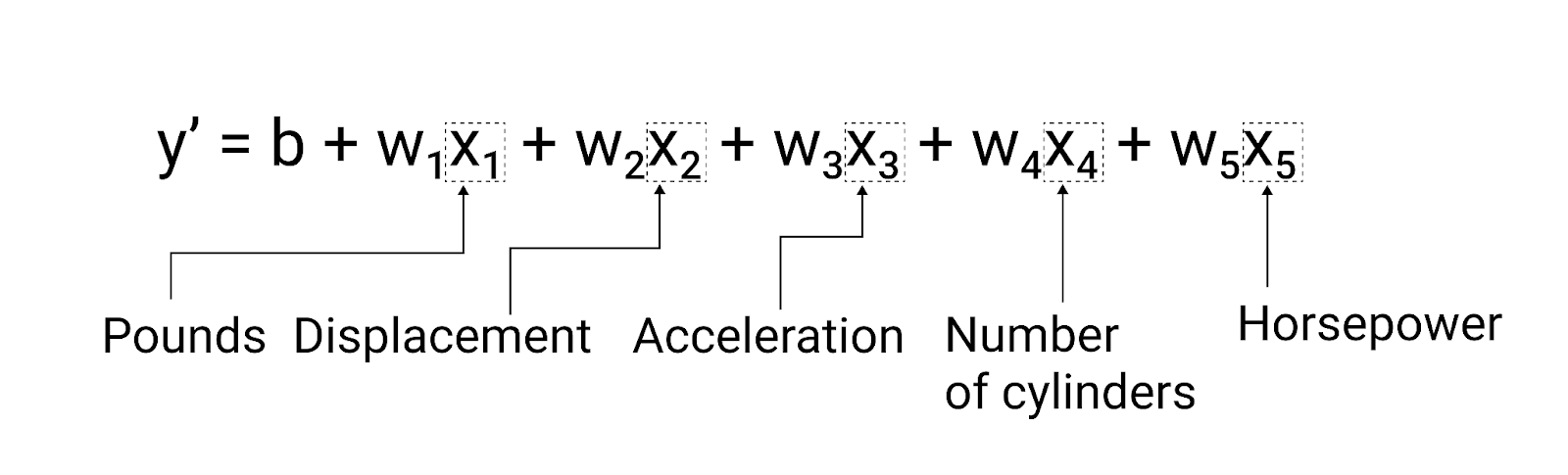
Hình 5. Một mô hình có 5 đặc điểm để dự đoán mức tiêu thụ nhiên liệu của ô tô (tính bằng dặm/gallon).
Bằng cách vẽ đồ thị một vài tính năng bổ sung này, chúng ta có thể thấy rằng chúng cũng có mối quan hệ tuyến tính với nhãn, số dặm trên một gallon:
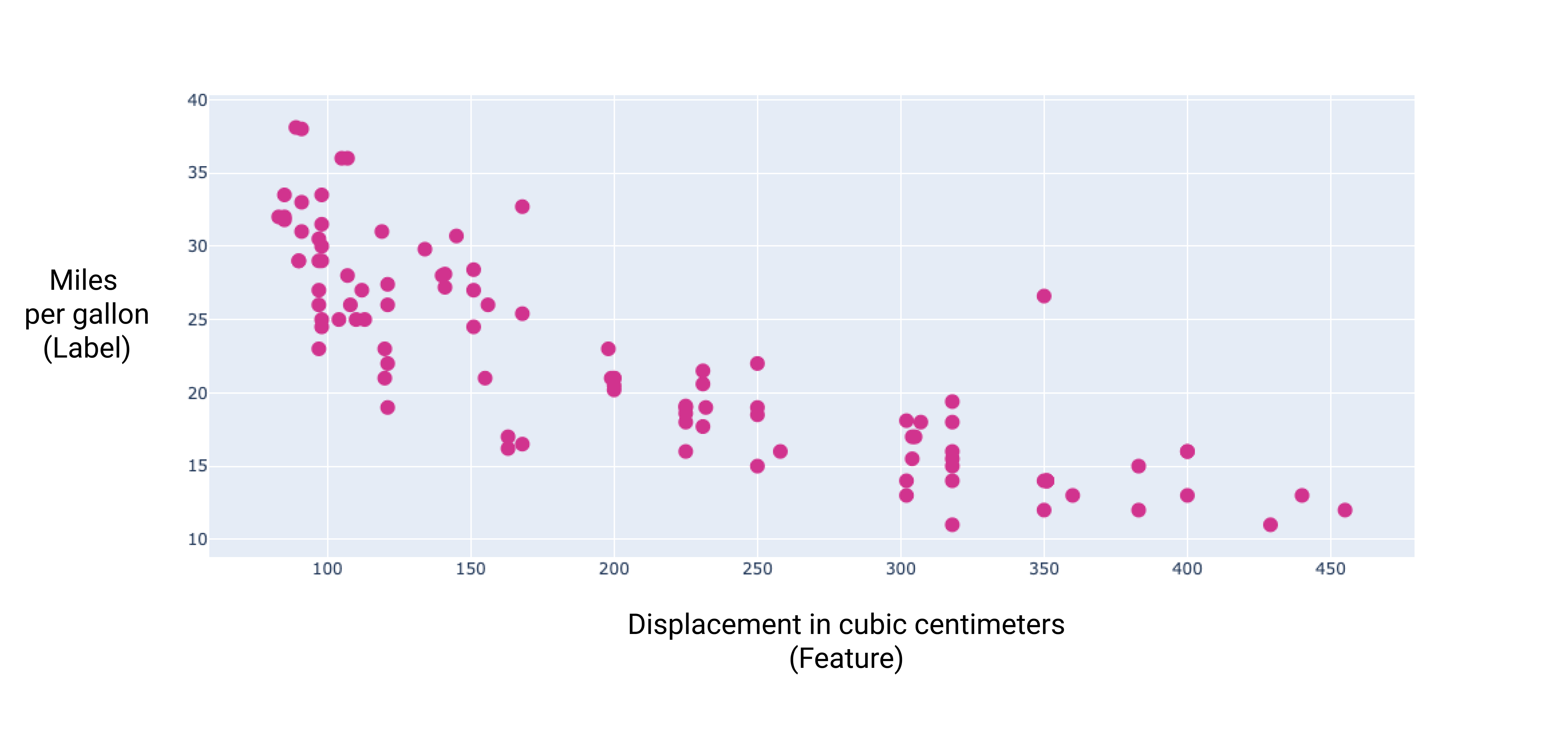
Hình 6. Dung tích xi lanh của ô tô tính bằng cm khối và mức tiêu thụ nhiên liệu tính bằng dặm/gallon. Khi động cơ của ô tô lớn hơn, chỉ số dặm/gallon thường giảm.
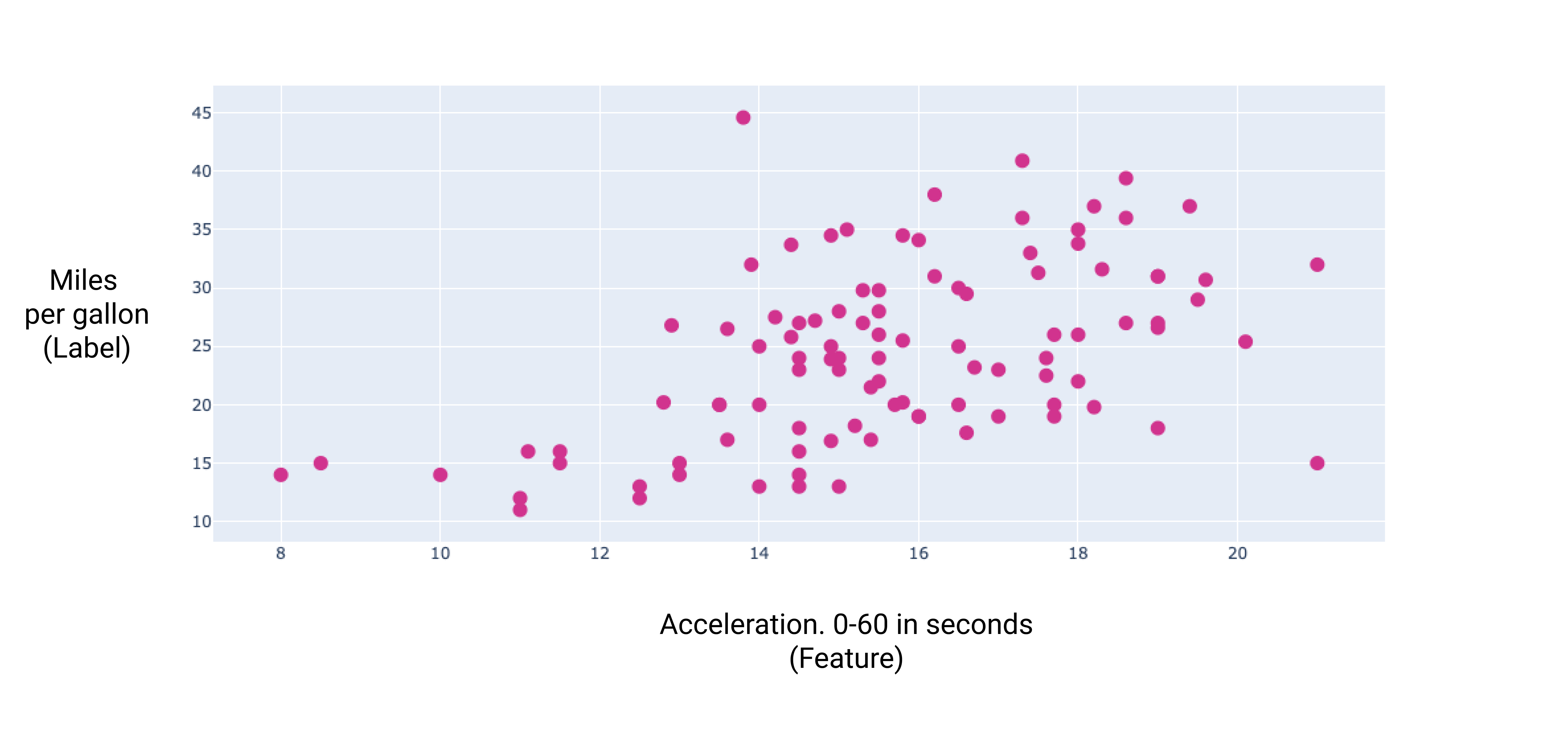
Hình 7. Gia tốc của ô tô và mức tiêu thụ nhiên liệu (dặm/gallon). Khi xe tăng tốc chậm hơn, chỉ số dặm/gallon thường tăng lên.