تقدّم هذه الوحدة مفاهيم الانحدار الخطي.
الانحدار الخطي هو أسلوب إحصائي يُستخدَم للعثور على العلاقة بين المتغيرات. في سياق تعلُّم الآلة، يحدّد الانحدار الخطي العلاقة بين الميزات والتصنيف.
على سبيل المثال، لنفترض أنّنا نريد التنبؤ بكفاءة استهلاك الوقود في سيارة بالكيلومترات لكل غالون استنادًا إلى وزن السيارة، ولدينا مجموعة البيانات التالية:
| الجنيهات بالآلاف (ميزة) | ميل لكل غالون (التصنيف) |
|---|---|
| 3.5 | 18 |
| 3.69 | 15 |
| 3.44 | 18 |
| 3.43 | 16 |
| 4.34 | 15 |
| 4.42 | 14 |
| 2.37 | 24 |
إذا رسمنا هذه النقاط، سنحصل على الرسم البياني التالي:
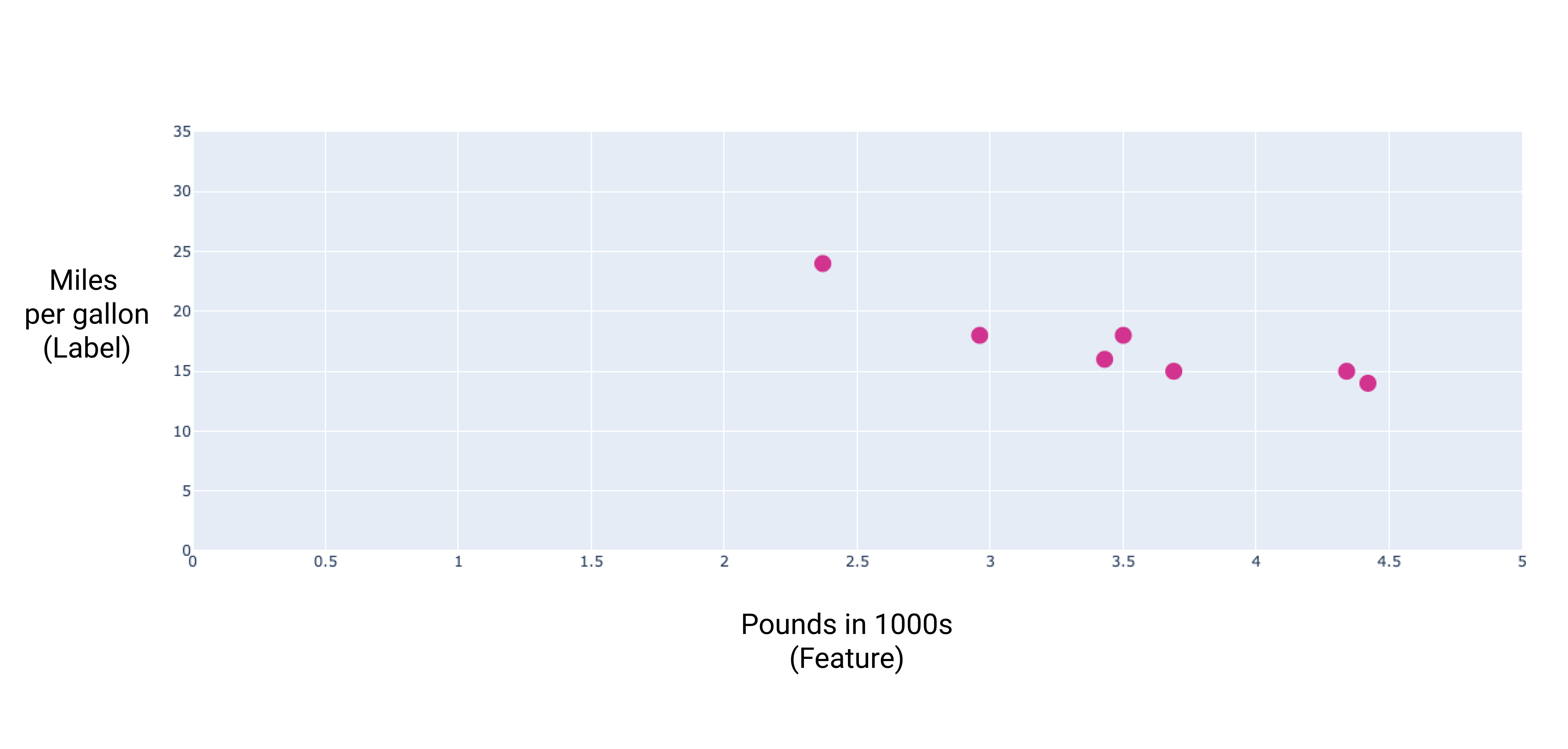
الشكل 1 وزن السيارة (بالرطل) مقارنةً بتقييم عدد الأميال المقطوعة لكل غالون بشكل عام، كلما زاد وزن السيارة، انخفض عدد الأميال التي يمكنها قطعها لكل غالون.
يمكننا إنشاء نموذجنا الخاص من خلال رسم خط أفضل ملاءمة عبر النقاط:
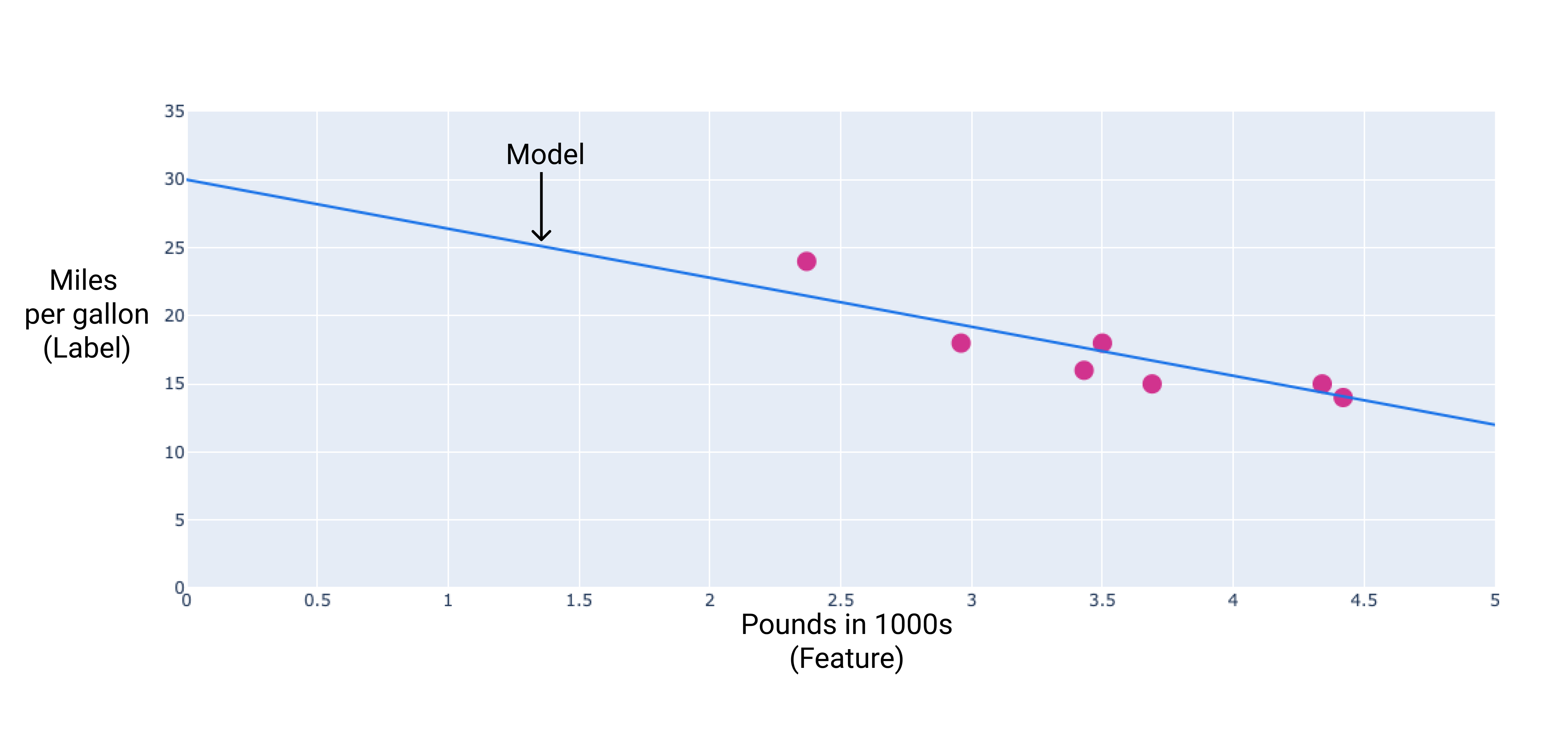
الشكل 2 خط أفضل تطابق مرسوم من خلال البيانات من الشكل السابق
معادلة الانحدار الخطي
من الناحية الجبرية، يتم تعريف النموذج على النحو التالي: $ y = mx + b $، حيث
- $ y $ هي عدد الأميال لكل غالون، وهي القيمة التي نريد التنبؤ بها.
- $ m $ هو مَيل الخط.
- $ x $ هي الجنيهات، وهي قيمة الإدخال.
- $ b $ هو نقطة التقاطع مع المحور y.
في تعلُّم الآلة، نكتب معادلة نموذج الانحدار الخطي على النحو التالي:
where:
- $ y' $ هي التصنيف المتوقّع، أي الناتج.
- $ b $ هو التحيّز للنموذج. التحيّز هو المفهوم نفسه الذي يمثّله الجزء المقطوع من المحور الصادي في المعادلة الجبرية للخط المستقيم. في تعلُّم الآلة، يُشار أحيانًا إلى التحيز بالرمز $ w_0 $. والتحيز هو مَعلمة للنموذج ويتم احتسابه أثناء التدريب.
- $ w_1 $ هو وزن الميزة. الوزن هو نفس مفهوم الميل $ m $ في المعادلة الجبرية للخط. الوزن هو مَعلمة للنموذج ويتم احتسابه أثناء التدريب.
- $ x_1 $ هي ميزة، أي المدخل.
أثناء التدريب، يحسب النموذج الوزن والانحياز اللذين ينتجان أفضل نموذج.
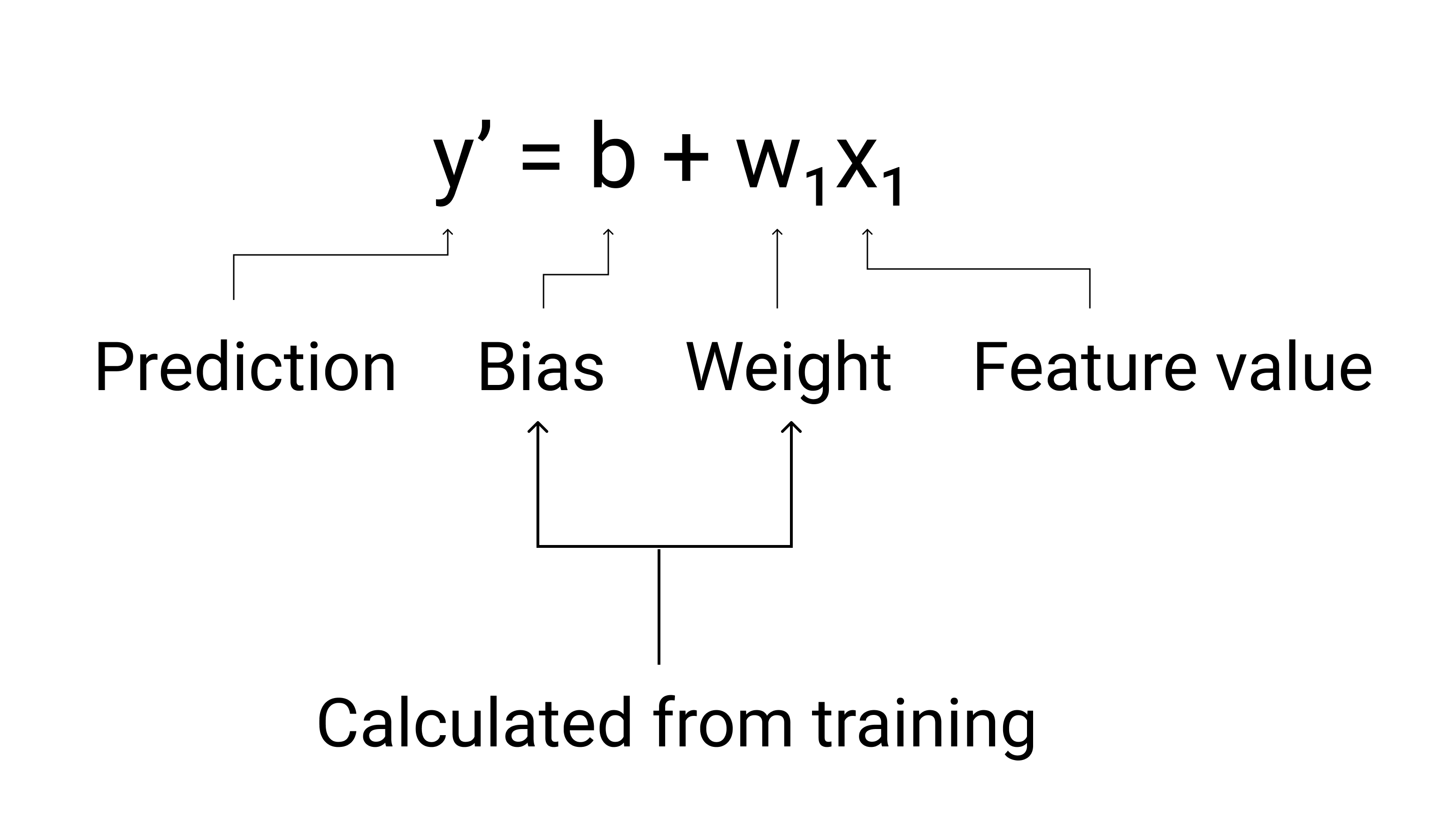
الشكل 3 تمثيل رياضي لنموذج خطي
في مثالنا، سنحسب الوزن والانحياز من الخط الذي رسمناه. التحيّز هو 34 (حيث يتقاطع الخط مع المحور y)، والوزن هو 4.6- (ميل الخط). سيتم تعريف النموذج على النحو التالي: $ y' = 34 + (-4.6)(x_1) $، ويمكننا استخدامه لتقديم التوقعات. على سبيل المثال، باستخدام هذا النموذج، ستحقّق سيارة تزن 4,000 رطل كفاءة في استهلاك الوقود تبلغ 15.6 ميل لكل غالون.
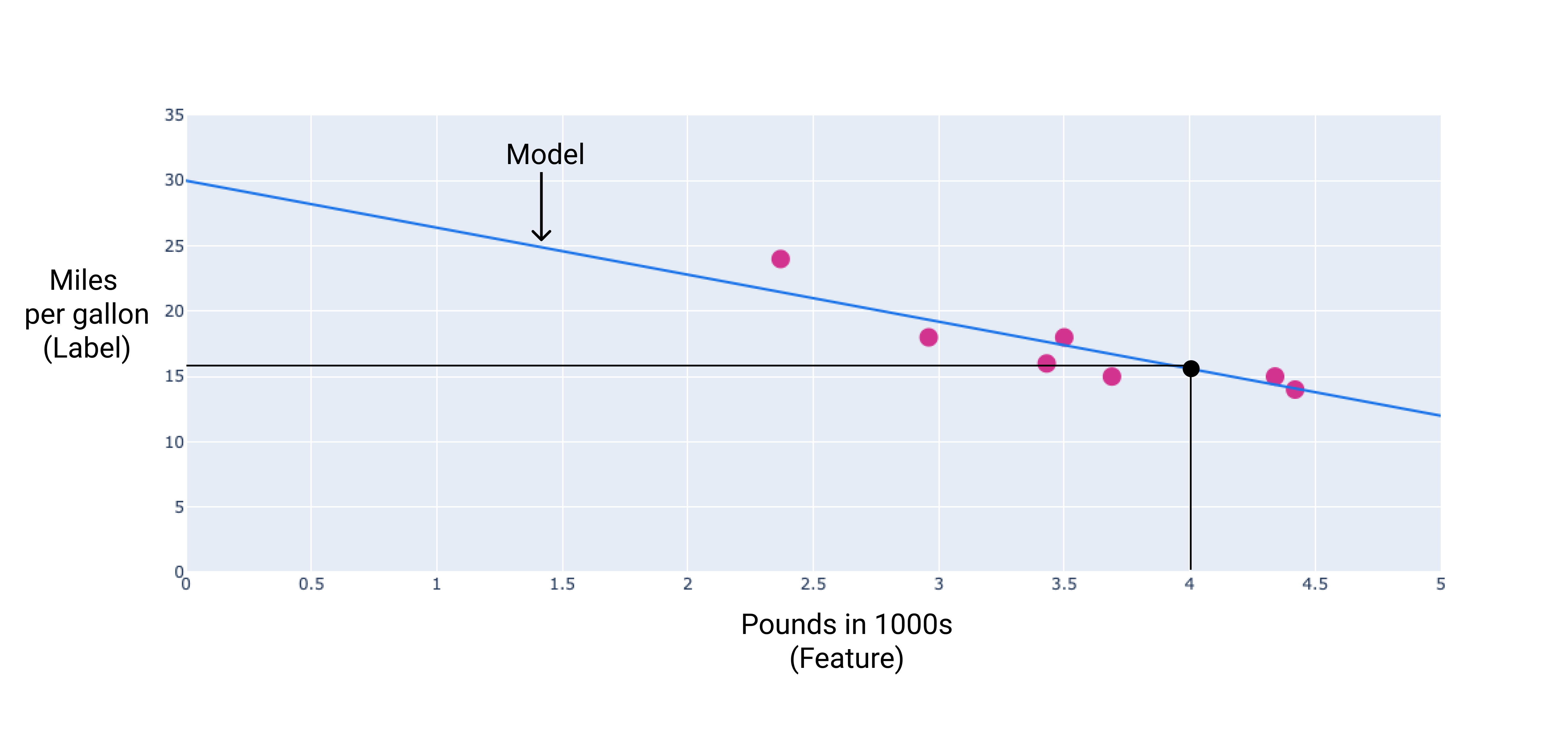
الشكل 4 باستخدام النموذج، تبلغ كفاءة استهلاك الوقود المتوقّعة لسيارة تزن 4,000 رطل 15.6 ميل لكل غالون.
النماذج التي تتضمّن ميزات متعدّدة
على الرغم من أنّ المثال الوارد في هذا القسم يستخدم ميزة واحدة فقط، وهي وزن السيارة، قد يعتمد نموذج أكثر تطورًا على ميزات متعددة، لكل منها وزن منفصل ($ w_1 $ و$ w_2 $ وما إلى ذلك). على سبيل المثال، سيتم كتابة نموذج يعتمد على خمس ميزات على النحو التالي:
$ y' = b + w_1x_1 + w_2x_2 + w_3x_3 + w_4x_4 + w_5x_5 $
على سبيل المثال، يمكن أن يستخدم نموذج يتوقّع عدد الكيلومترات التي يمكن قطعها بالغالون الواحد من الوقود ميزات إضافية، مثل ما يلي:
- سعة المحرك
- التسارع
- عدد الأسطوانات
- القدرة الحصانية
سيتم كتابة هذا النموذج على النحو التالي:
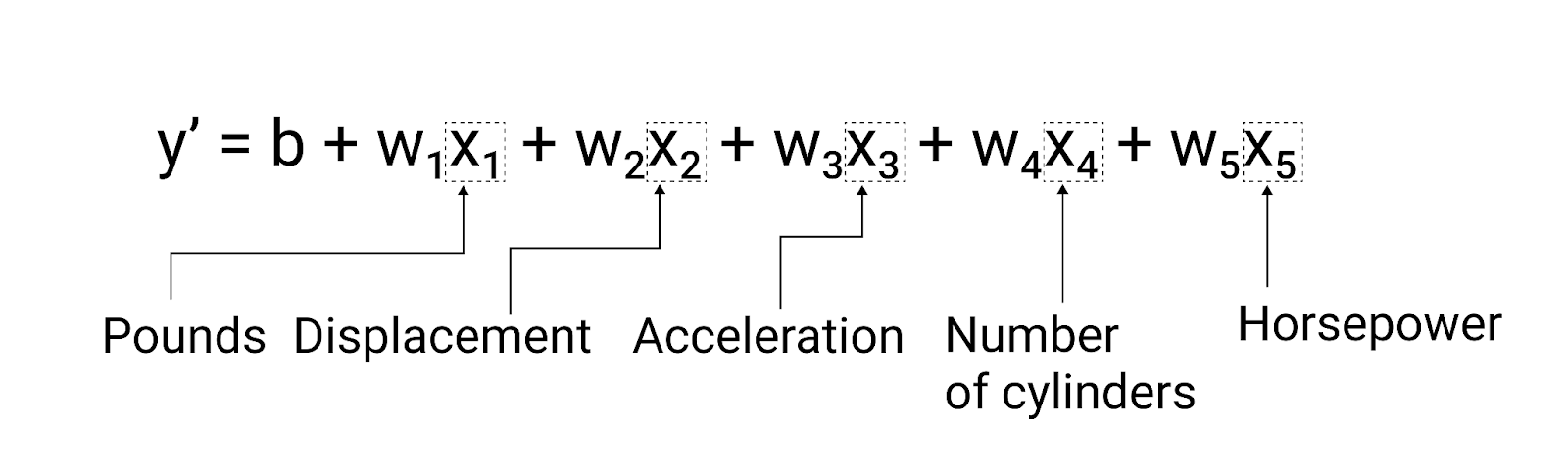
الشكل 5 نموذج يتضمّن خمس سمات للتنبؤ بتقييم عدد الأميال التي يمكن قطعها بغالون واحد من الوقود
من خلال رسم بياني لبعض هذه الميزات الإضافية، يمكننا أن نرى أنّها ترتبط أيضًا بشكل خطي بالتصنيف، أي عدد الأميال المقطوعة لكل غالون:
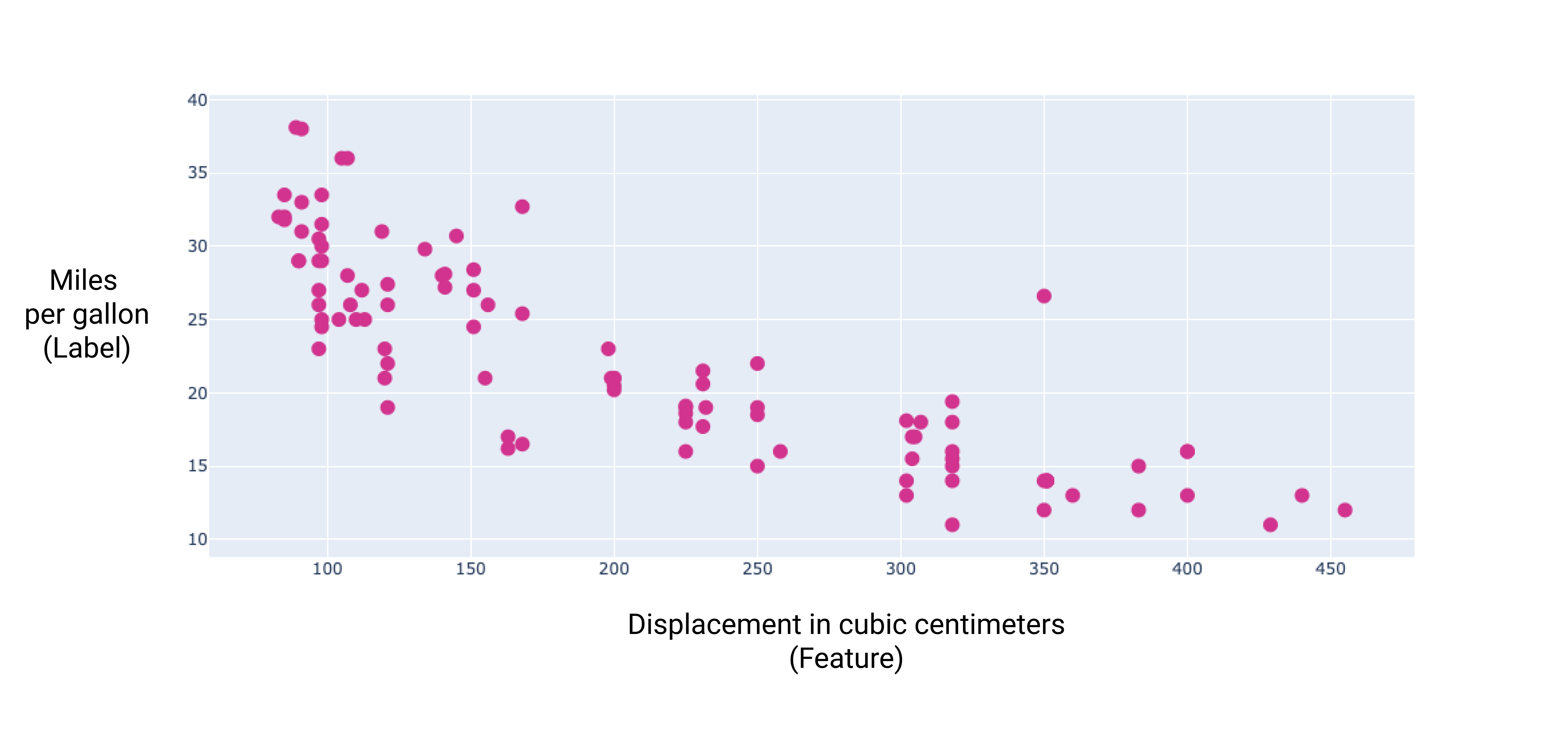
الشكل 6 إزاحة السيارة بالسنتيمتر المكعّب ومعدّل استهلاكها للوقود بالأميال لكل غالون كلما زاد حجم محرك السيارة، انخفض معدل استهلاكها للوقود.
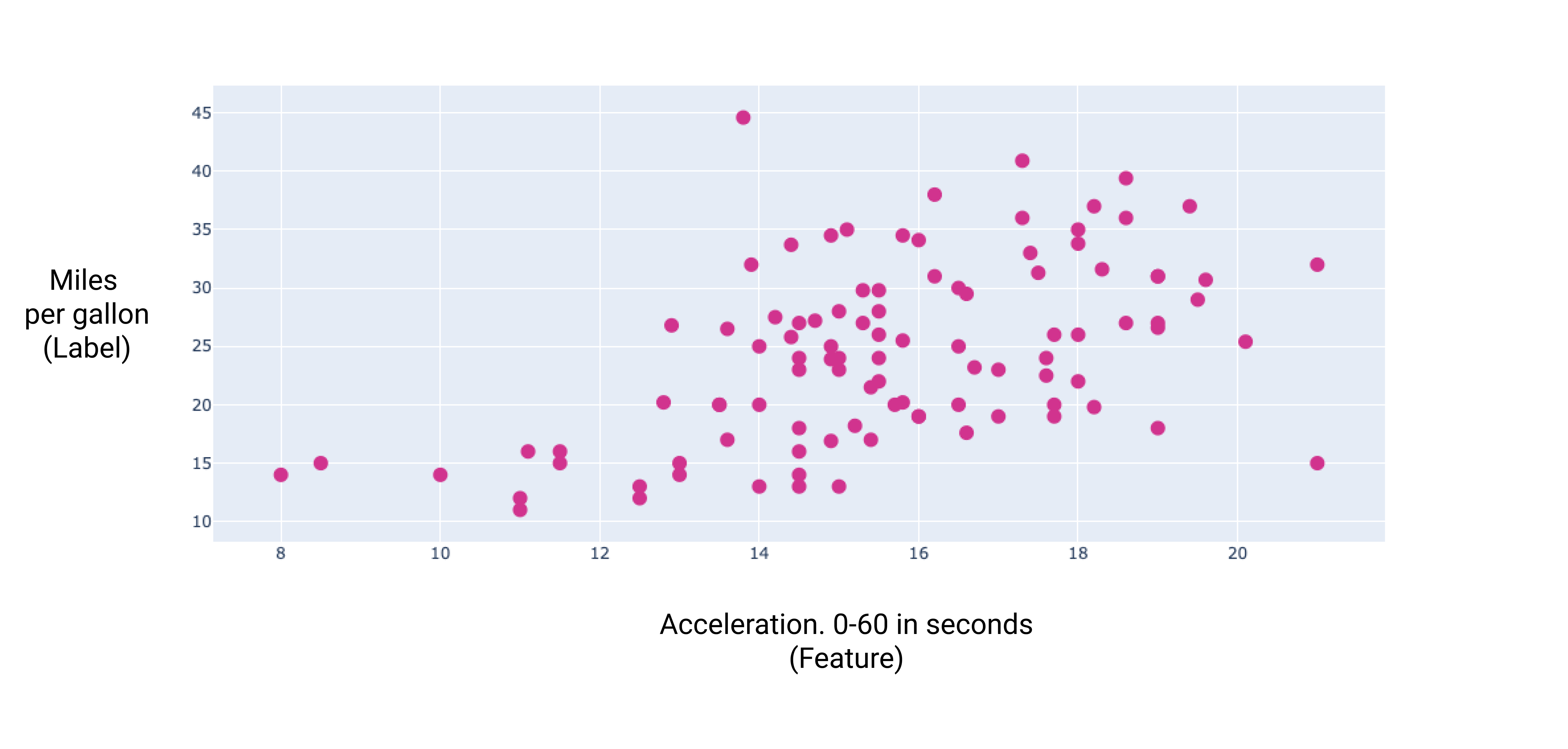
الشكل 7 تسارع السيارة ومعدّل استهلاكها للوقود كلما استغرقت السيارة وقتًا أطول في التسارع، زاد عدد الأميال التي يمكن قطعها لكل غالون بشكل عام.