이 모듈에서는 선형 회귀 개념을 소개합니다.
선형 회귀는 변수 간의 관계를 찾는 데 사용되는 통계 기법입니다. ML 컨텍스트에서 선형 회귀는 특성과 라벨 간의 관계를 찾습니다.
예를 들어 자동차의 무게를 기반으로 갤런당 마일로 자동차의 연비를 예측하려고 하고 다음과 같은 데이터 세트가 있다고 가정해 보겠습니다.
| 파운드(1,000단위)(기능) | 갤런당 마일(라벨) |
|---|---|
| 3.5 | 18 |
| 3.69 | 15 |
| 3.44 | 18 |
| 3.43 | 16 |
| 4.34 | 15 |
| 4.42 | 14 |
| 2.37 | 24 |
이러한 점을 그래프로 표시하면 다음과 같은 그래프가 됩니다.
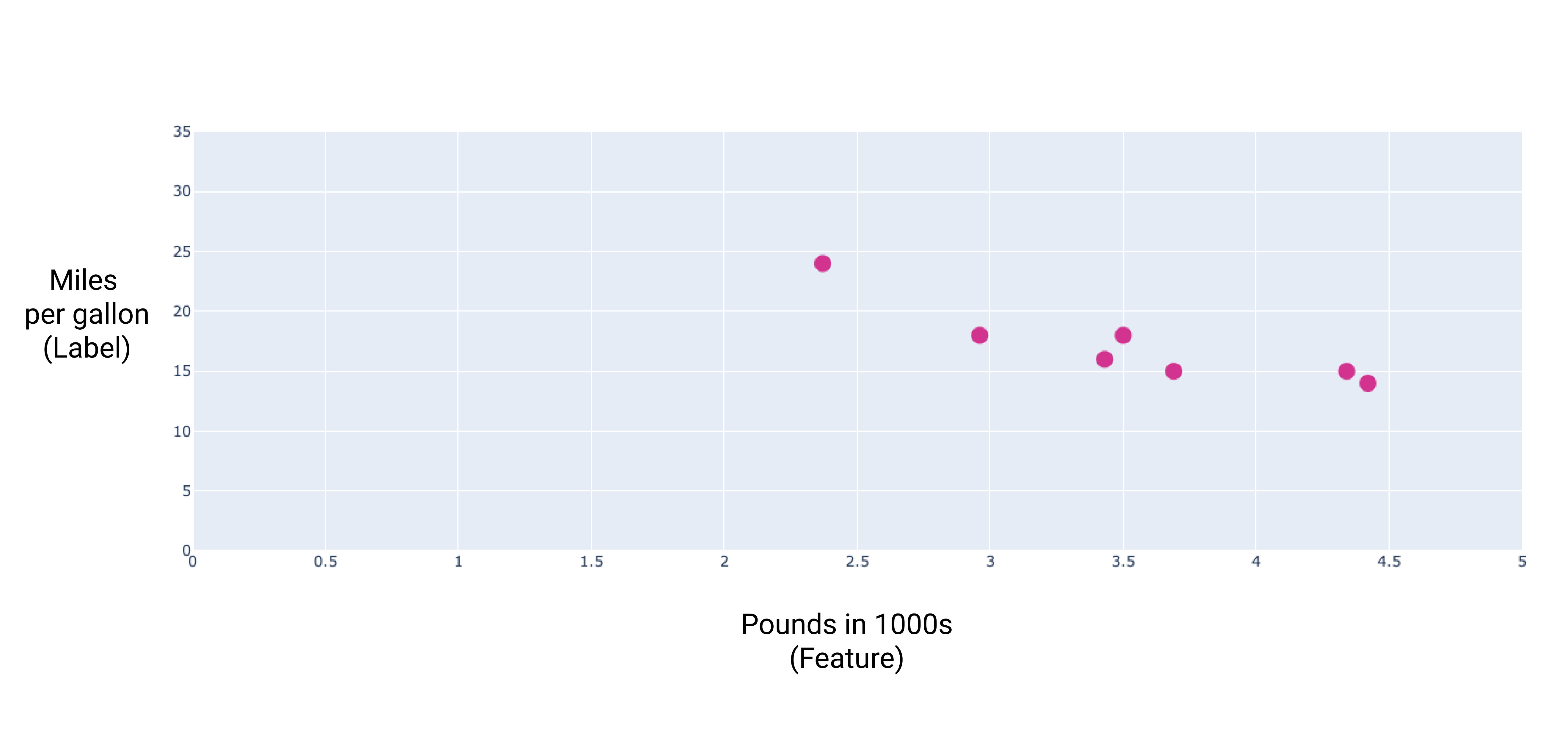
그림 1. 자동차 무게 (파운드)와 갤런당 마일 등급의 관계 자동차가 무거워지면 일반적으로 갤런당 마일 수가 줄어듭니다.
점을 통과하는 최적선을 그려 자체 모델을 만들 수 있습니다.
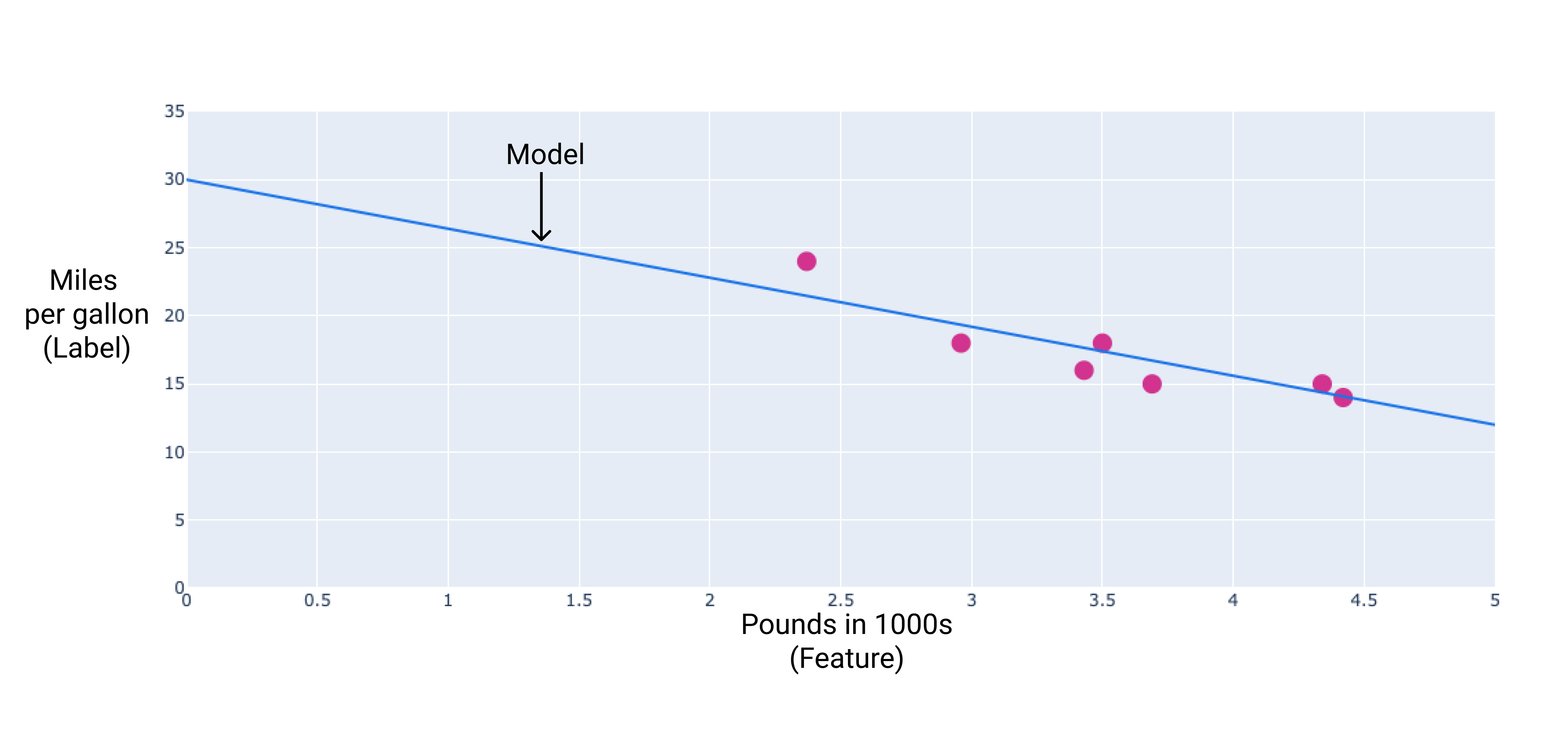
그림 2. 이전 그림의 데이터를 통해 그려진 최적선
선형 회귀 방정식
대수학적 용어로 모델은 $ y = mx + b $로 정의됩니다. 여기서
- $ y $ 는 갤런당 마일 수이며, 예측하려는 값입니다.
- $ m $ 은 선의 기울기입니다.
- $ x $ 는 파운드(입력 값)입니다.
- $ b $ 는 y절편입니다.
ML에서는 선형 회귀 모델의 방정식을 다음과 같이 작성합니다.
각 항목의 의미는 다음과 같습니다.
- $ y' $ 는 예측된 라벨(출력)입니다.
- $ b $ 는 모델의 편향입니다. 편향은 선의 대수 방정식에서 y 절편과 동일한 개념입니다. ML에서 편향은 $ w_0 $라고도 합니다. 편향은 모델의 매개변수이며 학습 중에 계산됩니다.
- $ w_1 $ 은 기능의 가중치입니다. 가중치는 선의 대수 방정식에서 기울기 $ m $ 과 동일한 개념입니다. 가중치는 모델의 매개변수이며 학습 중에 계산됩니다.
- $ x_1 $ 은 특성, 즉 입력입니다.
학습 중에 모델은 최적의 모델을 생성하는 가중치와 편향을 계산합니다.
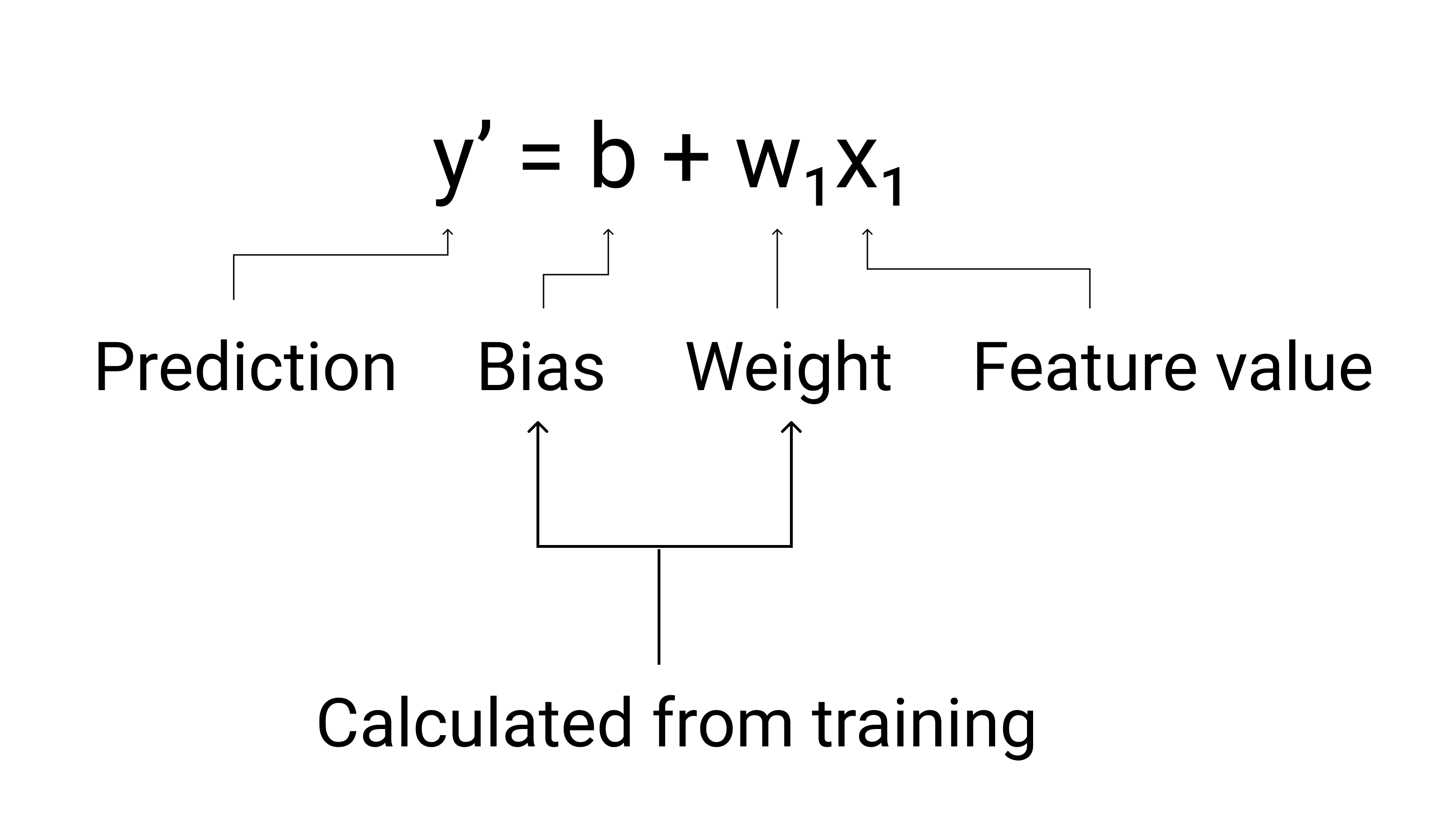
그림 3. 선형 모델의 수학적 표현입니다.
이 예시에서는 그린 선에서 가중치와 편향을 계산합니다. 편향은 34 (선이 y축과 교차하는 지점)이고 가중치는 -4.6 (선의 기울기)입니다. 모델은 $ y' = 34 + (-4.6)(x_1) $로 정의되며 이를 사용하여 예측할 수 있습니다. 예를 들어 이 모델을 사용하면 4,000파운드 자동차의 예상 연비는 갤런당 15.6마일입니다.
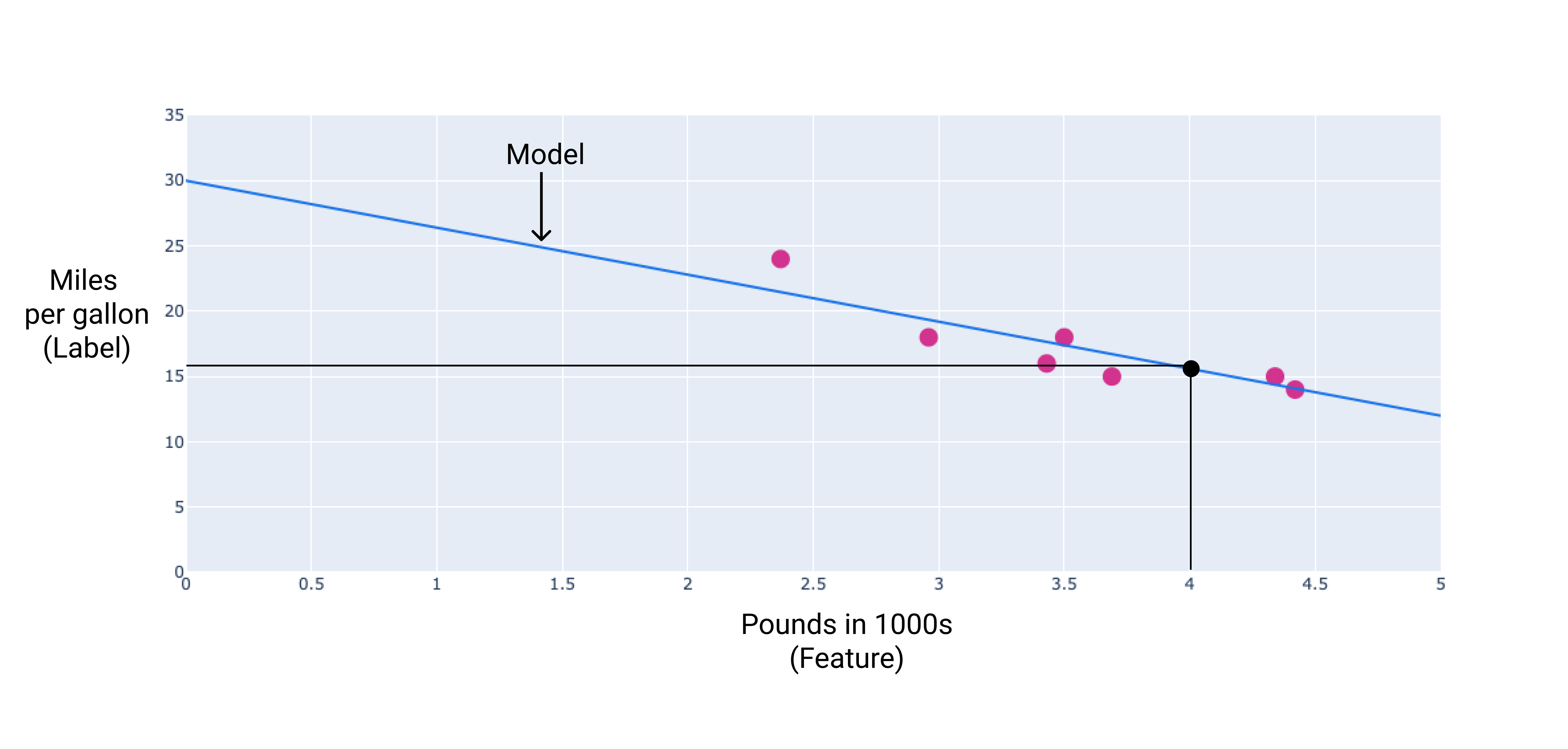
그림 4. 모델을 사용하면 4,000파운드 자동차의 예상 연비는 갤런당 15.6마일입니다.
기능이 여러 개인 모델
이 섹션의 예에서는 자동차의 무게라는 하나의 특성만 사용하지만 보다 정교한 모델에서는 별도의 가중치 ($ w_1 $, $ w_2 $, 등)가 있는 여러 개의 특성을 사용할 수도 있습니다. 예를 들어 5개의 특성을 사용하는 모델은 다음과 같이 작성됩니다.
$ y' = b + w_1x_1 + w_2x_2 + w_3x_3 + w_4x_4 + w_5x_5 $
예를 들어 연비를 예측하는 모델은 다음과 같은 기능을 추가로 사용할 수 있습니다.
- 엔진 배기량
- 가속
- 실린더 수
- 마력
이 모델은 다음과 같이 작성됩니다.
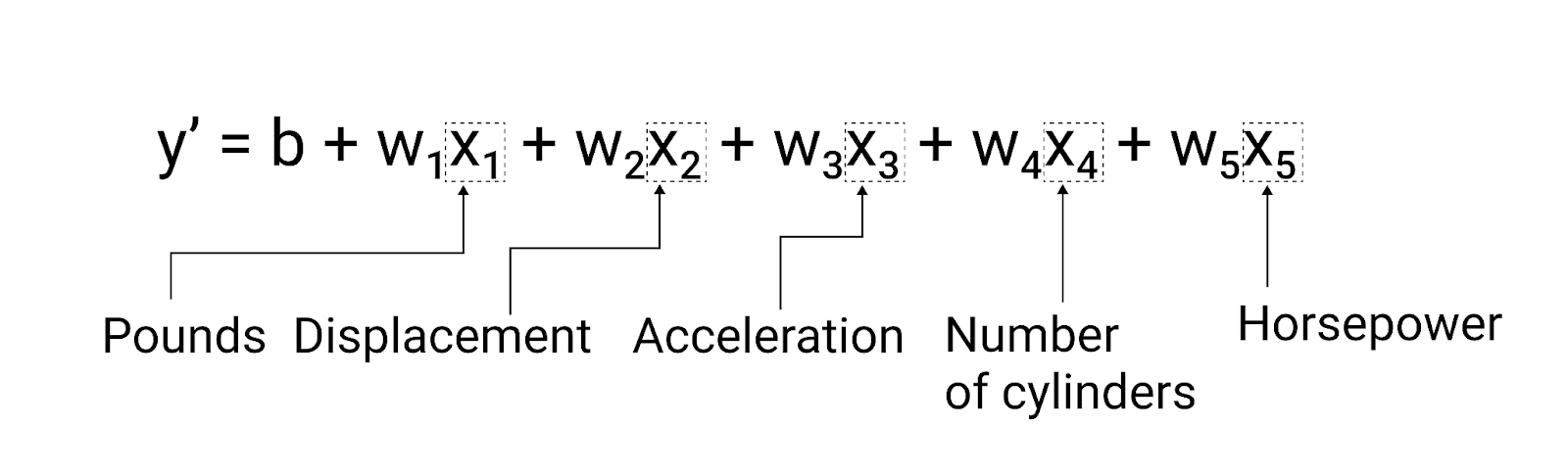
그림 5. 자동차의 갤런당 마일 등급을 예측하는 5가지 특징이 있는 모델
이러한 추가 기능을 몇 개 그래프로 표시하면 라벨인 갤런당 마일과 선형 관계가 있는 것을 확인할 수 있습니다.
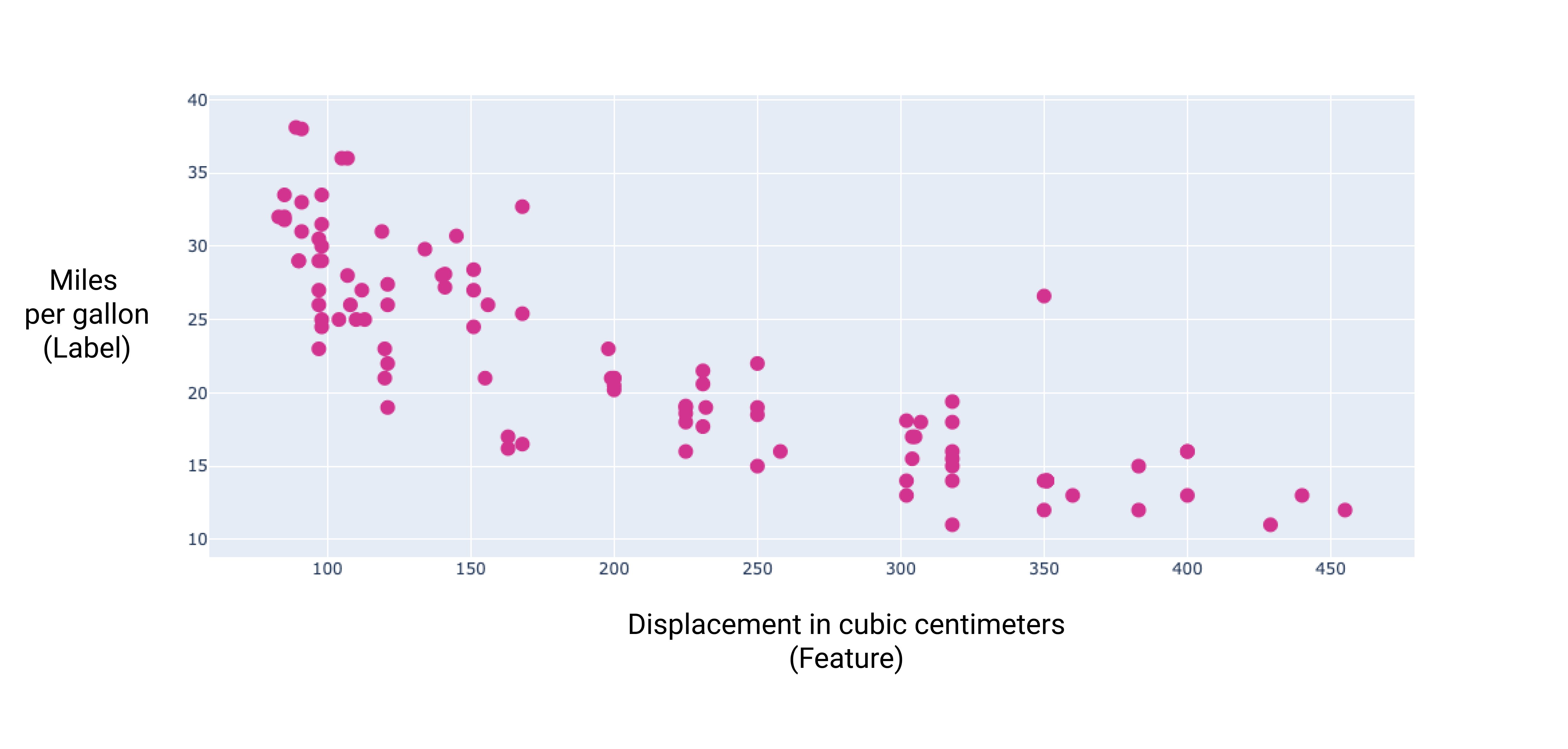
그림 6. 자동차의 배기량(단위: 입방센티미터)과 갤런당 마일 등급입니다. 자동차의 엔진이 커질수록 갤런당 마일 등급은 일반적으로 감소합니다.
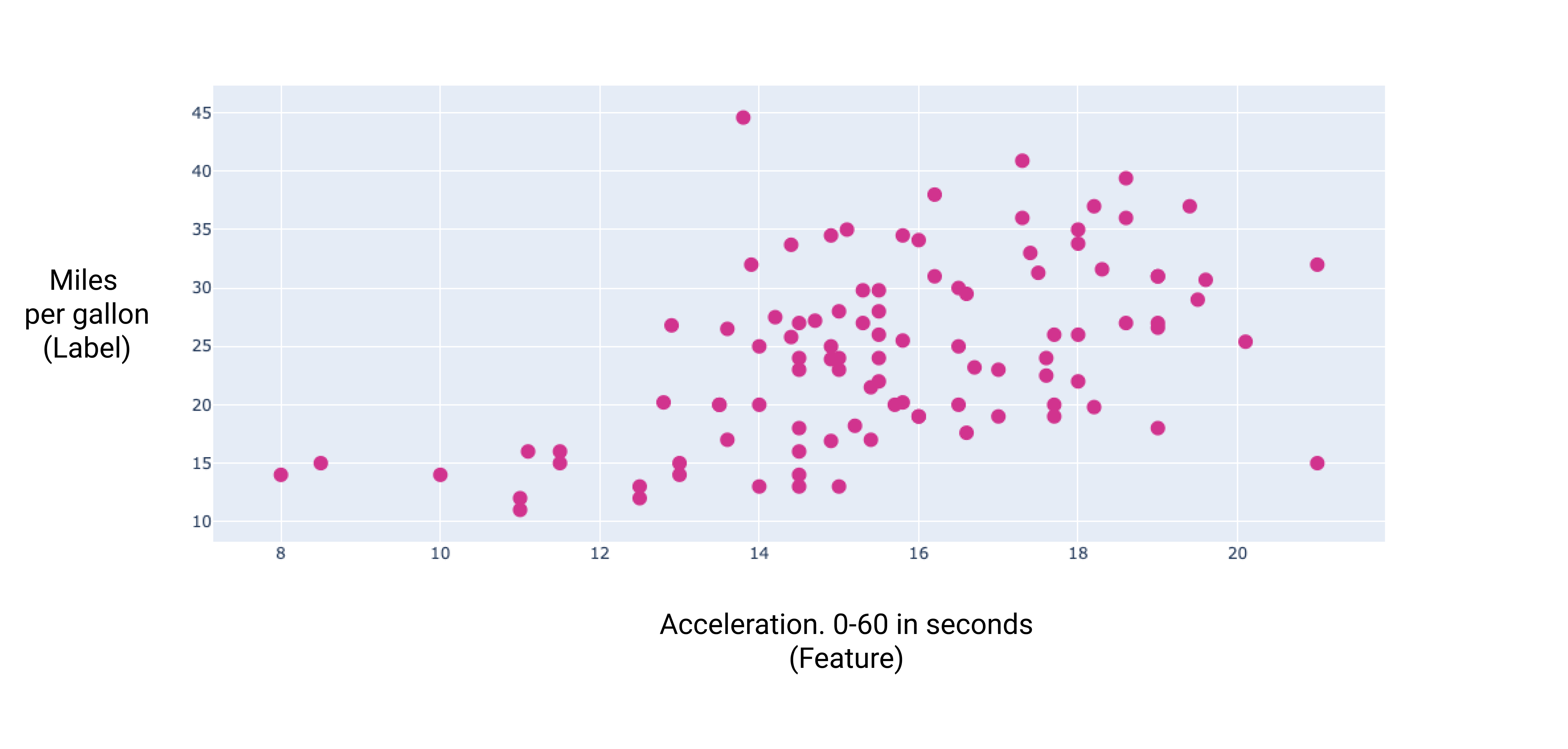
그림 7. 자동차의 가속도와 갤런당 마일 등급 자동차의 가속 시간이 길어질수록 일반적으로 갤런당 마일 등급이 높아집니다.