कई समस्याओं के लिए, आउटपुट के तौर पर संभावना का अनुमान ज़रूरी होता है. लॉजिस्टिक रिग्रेशन, संभावितताओं का हिसाब लगाने के लिए काफ़ी कारगर तरीका है. आम तौर पर, रिटर्न की गई संभावना का इस्तेमाल इनमें से किसी भी तरीके से किया जा सकता है:
"जैसा है" वैसा ही लागू होगा. उदाहरण के लिए, अगर कोई स्पैम-अनुमान मॉडल किसी ईमेल को
0.932की एक वैल्यू इनपुट और आउटपुट देता है, तो इससे93.2%की संभावना का पता चलता है कि यह स्पैम वाला ईमेल है.बाइनरी कैटगरी में बदला गया जैसे कि
TrueयाFalse,SpamयाNot Spam.
यह मॉड्यूल लॉजिस्टिक रिग्रेशन मॉडल आउटपुट के इस्तेमाल पर फ़ोकस करता है. इस क्लासिफ़िकेशन मॉड्यूल में, आपको इनके बारे में जानकारी मिलेगी इस आउटपुट को बाइनरी कैटगरी में बदलें.
सिगमॉइड फ़ंक्शन
आपको शायद यह जानना था कि लॉजिस्टिक रिग्रेशन मॉडल, आउटपुट को कैसे पक्का कर सकता है प्रॉबबिलिटी को दिखाता है. यह हमेशा 0 और 1 के बीच की वैल्यू देता है. लघुगणकीय फ़ंक्शन नाम के फ़ंक्शन की एक फ़ैमिली है, जिसके आउटपुट में ये सभी विशेषताएं होती हैं. स्टैंडर्ड लॉजिस्टिक फ़ंक्शन को सिग्मॉइड फ़ंक्शन भी कहा जाता है. सिग्मॉइड का मतलब "S-आकार" होता है. इसका फ़ॉर्मूला यह है:
\[f(x) = \frac{1}{1 + e^{-x}}\]
इमेज 1 में, सिगमॉइड फ़ंक्शन से जुड़ा संबंधित ग्राफ़ दिखाया गया है.
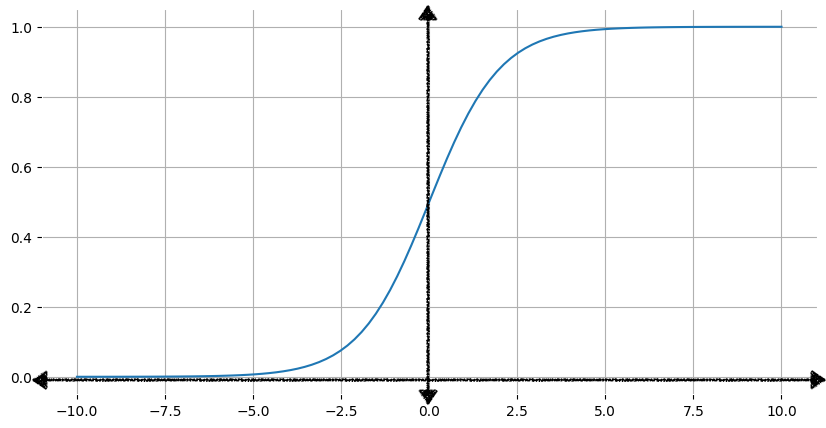
जब इनपुट के तौर पर x बढ़ जाता है, तब सिगमॉइड फ़ंक्शन का आउटपुट सामने आता है
लेकिन 1 तक कभी नहीं पहुंचता. इसी तरह, इनपुट कम होने पर, सिग्मॉइड
फ़ंक्शन का आउटपुट 0 के करीब पहुंचता है, लेकिन कभी उस तक नहीं पहुंचता.
गणित के बारे में ज़्यादा जानने के लिए यहां क्लिक करें सिगमॉइड फ़ंक्शन के पीछे
नीचे दी गई टेबल में, सिगमॉइड फ़ंक्शन के लिए आउटपुट वैल्यू दी गई है 7 से 7 की रेंज में वैल्यू डालें. ध्यान दें कि सिगमॉइड कितनी तेज़ी से पहुंचता है नेगेटिव इनपुट वैल्यू को कम करने और सिगमॉइड के करीब पहुंचने के लिए, 0 वैल्यू पॉज़िटिव इनपुट वैल्यू बढ़ाने के लिए 1.
हालांकि, इनपुट वैल्यू कितनी भी बड़ी या छोटी क्यों न हो, आउटपुट हमेशा 0 से ज़्यादा और 1 से कम होना चाहिए.
| इनपुट | सिगमॉइड आउटपुट |
|---|---|
| -7 | 0.001 |
| -6 | 0.002 |
| -5 | 0.007 |
| -4 | 0.018 |
| -3 | 0.047 |
| -2 | 0.119 |
| -1 | 0.269 |
| 0 | 0.50 |
| 1 | 0.731 |
| 2 | 0.881 |
| 3 | 0.952 |
| 4 | 0.982 |
| 5 | 0.993 |
| 6 | 0.997 |
| 7 | 0.999 |
सिग्मॉइड फ़ंक्शन का इस्तेमाल करके, लीनियर आउटपुट को ट्रांसफ़ॉर्म करना
नीचे दिया गया समीकरण, लॉजिस्टिक रिग्रेशन मॉडल के लीनियर कॉम्पोनेंट को दिखाता है:
\[z = b + w_1x_1 + w_2x_2 + \ldots + w_Nx_N\]
कहां:
- z, लीनियर इक्वेशन का आउटपुट है. इसे लॉग ऑड्स भी कहा जाता है.
- b, बायस है.
- w वैल्यू, मॉडल के सीखे गए वेट होती हैं.
- x वैल्यू, किसी खास उदाहरण के लिए सुविधा की वैल्यू होती हैं.
लॉजिस्टिक रिग्रेशन का अनुमान पाने के लिए, z वैल्यू को सिग्मॉइड फ़ंक्शन में पास किया जाता है. इससे 0 से 1 के बीच की वैल्यू (प्रोबैबिलिटी) मिलती है:
\[y' = \frac{1}{1 + e^{-z}}\]
कहां:
- y', लॉजिस्टिक रिग्रेशन मॉडल का आउटपुट है.
- z लीनियर आउटपुट है (जैसा कि पिछले समीकरण में कैलकुलेट किया गया है).
लॉग-ऑड्स के बारे में ज़्यादा जानने के लिए, यहां क्लिक करें
समीकरण $z = b + w_1x_1 + w_2x_2 + \ldots + w_Nx_N$ में, z को लॉग-ऑड्स कहा जाता है, क्योंकि अगर आप इस सिग्मॉइड फ़ंक्शन से शुरू करते हैं (जहां $y$, लॉजिस्टिक रिग्रेशन मॉडल का आउटपुट है, जो किसी संभावना को दिखाता है):
$$y = \frac{1}{1 + e^{-z}}$$
इसके बाद, z का मान ज्ञात करें:
$$ z = \log\left(\frac{y}{1-y}\right) $$
इसके बाद, z को दो संभावित नतीजों की संभावनाओं के अनुपात के लॉग के तौर पर परिभाषित किया जाता है: y और 1 – y.
दूसरी इमेज में दिखाया गया है कि इन कैलकुलेशन का इस्तेमाल करके, लीनियर आउटपुट को लॉजिस्टिक रिग्रेशन आउटपुट में कैसे बदला जाता है.
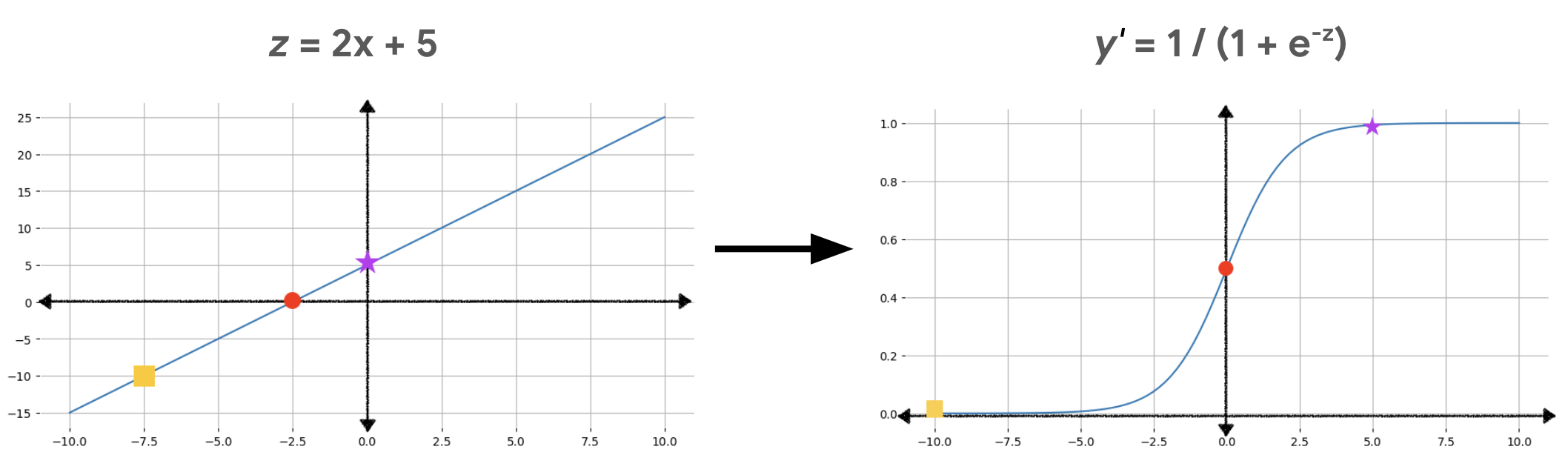
दूसरे चित्र में, एक लीनियर समीकरण सिग्मॉइड फ़ंक्शन का इनपुट बन जाता है, जो सीधी रेखा को एस-आकार में मोड़ देता है. ध्यान दें कि रैखिक समीकरण z के बहुत बड़े या बहुत छोटे मान हो सकते हैं, लेकिन सिगमॉइड का आउटपुट फ़ंक्शन, y', हमेशा 0 और 1 के बीच होता है, जिसमें यह शामिल नहीं है. उदाहरण के लिए, पीला बाएं ग्राफ़ के वर्ग का मान z –10 है, लेकिन इसमें सिग्मॉइड फ़ंक्शन है दायां ग्राफ़ जिसमें –10 को y' में दिखाया गया है वैल्यू 0.00004 है.
एक्सरसाइज़: देखें कि आपको क्या समझ आया
तीन सुविधाओं वाले लॉजिस्टिक रिग्रेशन मॉडल में, इनके लिए बायस और वज़न तय किए गए हैं:
\[\begin{align} b &= 1 \\ w_1 &= 2 \\ w_2 &= -1 \\ w_3 &= 5 \end{align} \]
इन इनपुट वैल्यू के लिए:
\[\begin{align} x_1 &= 0 \\ x_2 &= 10 \\ x_3 &= 2 \end{align} \]
नीचे दिए गए दो सवालों के जवाब दें.
जैसा कि ऊपर #1 में बताया गया है, इनपुट वैल्यू का लॉग-ऑड 1 है. z की उस वैल्यू को सिग्मॉइड फ़ंक्शन में डालें:
\(y = \frac{1}{1 + e^{-z}} = \frac{1}{1 + e^{-1}} = \frac{1}{1 + 0.367} = \frac{1}{1.367} = 0.731\)
