หลายๆ ปัญหาต้องการค่าประมาณความน่าจะเป็นที่เป็นเอาต์พุต การถดถอยแบบโลจิสติกส์คือ กลไกที่มีประสิทธิภาพมากในการคำนวณความน่าจะเป็น ในทางปฏิบัติ คุณสามารถใช้ความน่าจะเป็นที่แสดงผลได้ 2 วิธีดังนี้
ใช้ "ตามที่เป็นอยู่" ตัวอย่างเช่น หากโมเดลการคาดคะเนสแปมใช้อีเมลเป็น ป้อนค่า
0.932และแสดงความน่าจะเป็น93.2%อีเมลดังกล่าวเป็นจดหมายขยะแปลงเป็นหมวดหมู่ไบนารีแล้ว เช่น
TrueหรือFalse,SpamหรือNot Spam
โมดูลนี้มุ่งเน้นที่การใช้เอาต์พุตโมเดลการถดถอยแบบโลจิสติกตามที่มีอยู่ ใน โมดูลการแยกประเภท คุณจะได้เรียนรู้วิธีการ แปลงเอาต์พุตนี้เป็นหมวดหมู่ไบนารี
ฟังก์ชันซิกมอยด์
คุณอาจสงสัยว่าโมเดลการถดถอยเชิงโลจิสติกส์จะแน่ใจได้อย่างไรว่าเอาต์พุตแสดงถึงความน่าจะเป็น โดยแสดงค่าระหว่าง 0 ถึง 1 เสมอ ตามที่เห็น จะมีฟังก์ชันส่วนหนึ่งที่เรียกว่าฟังก์ชันโลจิสติก ซึ่งเอาต์พุตจะมีลักษณะเดียวกันนี้ ฟังก์ชันโลจิสติกมาตรฐาน หรือที่เรียกว่าฟังก์ชัน Sigmoid (Sigmoid หมายถึง "รูปตัว S") มีสูตรดังนี้
\[f(x) = \frac{1}{1 + e^{-x}}\]
รูปที่ 1 แสดงกราฟที่สอดคล้องกันของฟังก์ชัน Sigmoid
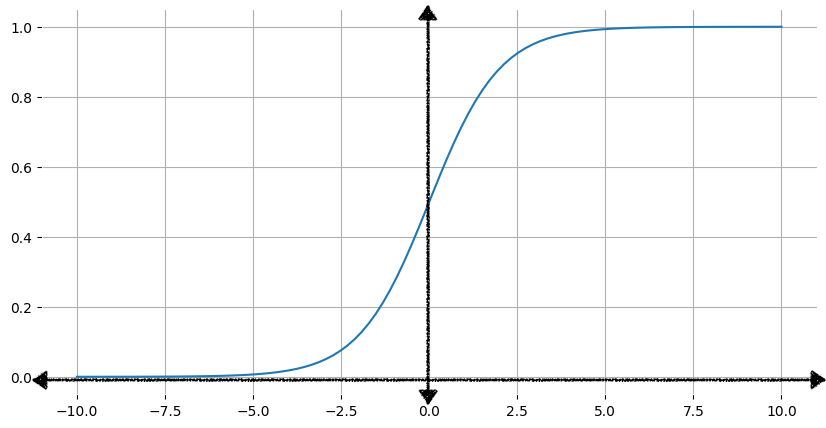
เมื่ออินพุต x เพิ่มขึ้น เอาต์พุตของฟังก์ชัน Sigmoid จะเข้าใกล้
แต่ไม่เคยถึง 1 ในทำนองเดียวกัน เมื่ออินพุตลดลง เอาต์พุตของฟังก์ชัน Sigmoid จะเข้าใกล้แต่ไม่เคยถึง 0
คลิกที่นี่เพื่อดูรายละเอียดเพิ่มเติมเกี่ยวกับคณิตศาสตร์ที่อยู่เบื้องหลังฟังก์ชัน Sigmoid
ตารางด้านล่างแสดงค่าเอาต์พุตของฟังก์ชัน Sigmoid สำหรับค่าอินพุตในช่วง -7 ถึง 7 สังเกตว่า Sigmoid เข้าใกล้ 0 เร็วเพียงใดเมื่อค่าอินพุตเป็นลบ และเข้าใกล้ 1 เร็วเพียงใดเมื่อค่าอินพุตเป็นบวก
อย่างไรก็ตาม ไม่ว่าค่าอินพุตจะมากหรือน้อยเพียงใด เอาต์พุตจะมากกว่า 0 และน้อยกว่า 1 เสมอ
| อินพุต | เอาต์พุต Sigmoid |
|---|---|
| -7 | 0.001 |
| -6 | 0.002 |
| -5 | 0.007 |
| -4 | 0.018 |
| -3 | 0.047 |
| -2 | 0.119 |
| -1 | 0.269 |
| 0 | 0.50 |
| 1 | 0.731 |
| 2 | 0.881 |
| 3 | 0.952 |
| 4 | 0.982 |
| 5 | 0.993 |
| 6 | 0.997 |
| 7 | 0.999 |
การแปลงเอาต์พุตเชิงเส้นโดยใช้ฟังก์ชัน Sigmoid
สมการต่อไปนี้แสดงส่วนประกอบเชิงเส้นของโลจิสติกส์ โมเดลการถดถอย:
\[z = b + w_1x_1 + w_2x_2 + \ldots + w_Nx_N\]
where:
- z คือเอาต์พุตของสมการเชิงเส้น หรือที่เรียกกันว่า ความเป็นไปได้ในการบันทึก
- b คือความเอนเอียง
- ค่า w คือน้ำหนักที่โมเดลเรียนรู้แล้ว
- ค่า x คือค่าฟีเจอร์สำหรับตัวอย่างที่เฉพาะเจาะจง
ในการรับการคาดการณ์การถดถอยแบบโลจิสติก ระบบจะส่งค่า z ไปยัง ฟังก์ชันซิกมอยด์ จะแสดงค่า (ความน่าจะเป็น) ระหว่าง 0 ถึง 1 ดังนี้
\[y' = \frac{1}{1 + e^{-z}}\]
where:
- y' คือเอาต์พุตของโมเดลการถดถอยแบบโลจิสติก
- z คือเอาต์พุตเชิงเส้น (ตามที่คํานวณในสมการก่อนหน้า)
คลิกที่นี่เพื่อดูข้อมูลเพิ่มเติมเกี่ยวกับอัตราส่วนโอกาสเชิงลอจิก
ในสมการ $z = b + w_1x_1 + w_2x_2 + \ldots + w_Nx_N$ นั้น z จะเรียกว่า Log-Odds เนื่องจากหากคุณเริ่มต้นด้วยฟังก์ชัน Sigmoid ต่อไปนี้ (โดยที่ $y$ คือเอาต์พุตของโมเดลการถดถอยเชิงโลจิสติก ซึ่งแสดงถึงค่าความน่าจะเป็น)
$$y = \frac{1}{1 + e^{-z}}$$
แล้วแก้โจทย์ด้วย z
$$ z = \log\left(\frac{y}{1-y}\right) $$
จากนั้น z หมายถึงบันทึกของอัตราส่วนของความน่าจะเป็น ของผลลัพธ์ที่เป็นไปได้ 2 รายการ ได้แก่ y และ 1 – y
รูปที่ 2 แสดงวิธีเปลี่ยนรูปแบบเอาต์พุตเชิงเส้นเป็นเอาต์พุตการประมาณเชิงเส้นโลจิสติกโดยใช้การคํานวณเหล่านี้
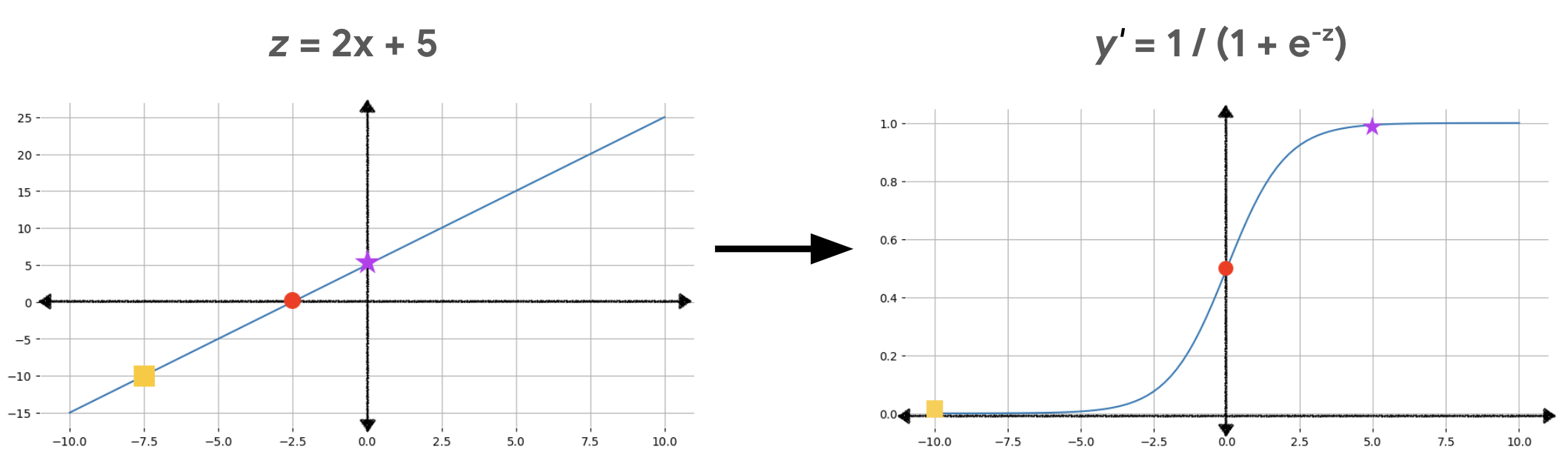
ในรูปที่ 2 สมการเชิงเส้นกลายเป็นอินพุตไปยังฟังก์ชันซิกมอยด์ ซึ่งจะบิดเส้นตรงให้เป็นรูปตัว S โปรดสังเกตว่าสมการเชิงเส้น จะแสดงค่า z ที่มีขนาดใหญ่หรือเล็กมากได้ แต่เอาต์พุตของ sigmoid y' จะอยู่ระหว่าง 0 ถึง 1 เสมอ เช่น สี่เหลี่ยมจัตุรัสสีเหลืองในกราฟด้านซ้ายมีค่า z เป็น –10 แต่ฟังก์ชัน Sigmoid ในกราฟด้านขวาจับคู่ –10 นั้นให้เป็นค่า y' ที่ 0.00004
แบบฝึกหัด: ทดสอบความเข้าใจ
โมเดลการถดถอยเชิงลอจิสติกที่มี 3 ฟีเจอร์มีน้ำหนักและค่ากําหนดดังนี้
\[\begin{align} b &= 1 \\ w_1 &= 2 \\ w_2 &= -1 \\ w_3 &= 5 \end{align} \]
ได้มาจากค่าอินพุตต่อไปนี้
\[\begin{align} x_1 &= 0 \\ x_2 &= 10 \\ x_3 &= 2 \end{align} \]
ตอบคำถาม 2 ข้อต่อไปนี้
ตามที่คำนวณในข้อ 1 ข้างต้น โอกาสในบันทึกสำหรับค่าอินพุตคือ 1 การเสียบค่า z นั้นเข้ากับฟังก์ชัน sigmoid
\(y = \frac{1}{1 + e^{-z}} = \frac{1}{1 + e^{-1}} = \frac{1}{1 + 0.367} = \frac{1}{1.367} = 0.731\)
