Regresja logistyczna: obliczanie prawdopodobieństwa za pomocą funkcji sigmoidalnej

Wiele problemów wymaga oszacowania prawdopodobieństwa jako danych wyjściowych. Regresja logistyczna to bardzo wydajny mechanizm obliczania prawdopodobieństw. W praktyce zwrócone prawdopodobieństwo możesz wykorzystać na 2 sposoby:

• Zastosowano „w takiej postaci, w jakiej jest”. Jeśli na przykład model prognozujący spam przyjmuje e-maila jako dane wejściowe i generuje wartość 0.932, oznacza to, że prawdopodobieństwo, że e-mail jest spamem, wynosi 93.2%.

• Przekształcone w kategorię binarną, np. True lub False, Spam lub Not Spam.

W tym module skupimy się na używaniu danych wyjściowych modelu regresji logistycznej w ich pierwotnej postaci. W module Klasyfikacja dowiesz się, jak przekształcić te dane wyjściowe w kategorię binarną.

Funkcja sigmoid

Być może zastanawiasz się, jak model regresji logistycznej może zapewnić, że jego dane wyjściowe reprezentują prawdopodobieństwo, zawsze zwracając wartość z zakresu od 0 do 1. Istnieje rodzina funkcji zwanych funkcjami logistycznymi, których dane wyjściowe mają te same cechy. Standardowa funkcja logistyczna, znana też jako funkcja sigmoidalna (sigmoid oznacza „w kształcie litery S”), ma postać:

\[f(x) = \frac{1}{1 + e^{-x}}\]

gdzie:

• f(x) to wynik funkcji sigmoid.
• e to liczba Eulera: stała matematyczna ≈ 2,71828.
• x to dane wejściowe funkcji sigmoid.

Na rysunku 1 przedstawiono odpowiedni wykres funkcji sigmoid.

Rysunek 1. Wykres funkcji sigmoid. Krzywa zbliża się do 0, gdy wartości x maleją do minus nieskończoności, a do 1, gdy wartości x rosną do nieskończoności.

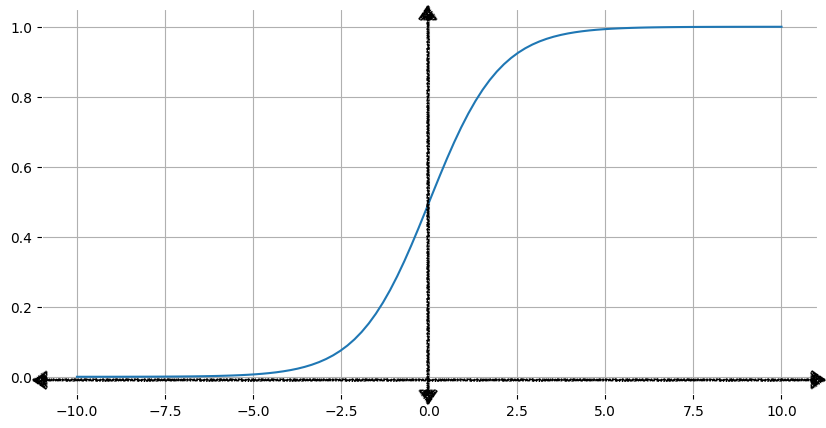
Wraz ze wzrostem wartości wejściowej x wartość wyjściowa funkcji sigmoid zbliża się do 1, ale nigdy jej nie osiąga. Podobnie, gdy wartość wejściowa maleje, wartość wyjściowa funkcji sigmoidalnej zbliża się do 0, ale nigdy jej nie osiąga.

Kliknij tutaj, aby dowiedzieć się więcej o matematyce funkcji sigmoidalnej

W tabeli poniżej znajdziesz wartości wyjściowe funkcji sigmoidalnej dla wartości wejściowych z zakresu od –7 do 7. Zwróć uwagę, jak szybko funkcja sigmoidalna zbliża się do 0 w przypadku malejących ujemnych wartości wejściowych i jak szybko zbliża się do 1 w przypadku rosnących dodatnich wartości wejściowych.

Niezależnie od tego, jak duża lub mała jest wartość wejściowa, wartość wyjściowa będzie zawsze większa od 0 i mniejsza od 1.

Dane wejściowe	Dane wyjściowe funkcji sigmoid
-7	0,001
-6	0,002
-5	0,007
-4	0,018
-3	0,047
-2	0.119
-1	0,269
0	0,50
1	0,731
2	0,881
3	0,952
4	0,982
5	0,993
6	0,997
7	0,999

Przekształcanie danych wyjściowych liniowych za pomocą funkcji sigmoid

Poniższe równanie przedstawia komponent liniowy modelu regresji logistycznej:

\[z = b + w_1x_1 + w_2x_2 + \ldots + w_Nx_N\]

gdzie:

• z to wynik równania liniowego, zwany też logarytmem szans.
• b to odchylenie.
• Wartości w to wagi wyuczone przez model.
• Wartości x to wartości cech dla konkretnego przykładu.

Aby uzyskać prognozę na podstawie regresji logistycznej, wartość z jest następnie przekazywana do funkcji sigmoidalnej, co daje wartość (prawdopodobieństwo) z przedziału od 0 do 1:

\[y' = \frac{1}{1 + e^{-z}}\]

gdzie:

• y' to dane wyjściowe modelu regresji logistycznej.
• e to liczba Eulera: stała matematyczna ≈ 2,71828.
• z to wynik liniowy (obliczony w poprzednim równaniu).

Kliknij tutaj, aby dowiedzieć się więcej o log-odds

W równaniu $z = b + w_1x_1 + w_2x_2 + \ldots + w_Nx_N$ zmienna z jest nazywana logarytmem szans, ponieważ jeśli zaczniesz od tej funkcji sigmoidalnej (gdzie $y$ to wynik modelu regresji logistycznej, który reprezentuje prawdopodobieństwo):

$$y = \frac{1}{1 + e^{-z}}$$

Następnie rozwiąż równanie ze względu na z:

$$ z = \ln\left(\frac{y}{1-y}\right) $$

Wtedy z jest zdefiniowane jako logarytm naturalny stosunku prawdopodobieństw dwóch możliwych wyników: y i 1 – y.

Rysunek 2 pokazuje, jak za pomocą tych obliczeń liniowy wynik jest przekształcany w wynik regresji logistycznej.

Rysunek 2. Po lewej: wykres funkcji liniowej z = 2x + 5 z zaznaczonymi 3 punktami. Po prawej: krzywa sigmoidalna z tymi samymi 3 punktami wyróżnionymi po przekształceniu przez funkcję sigmoid.

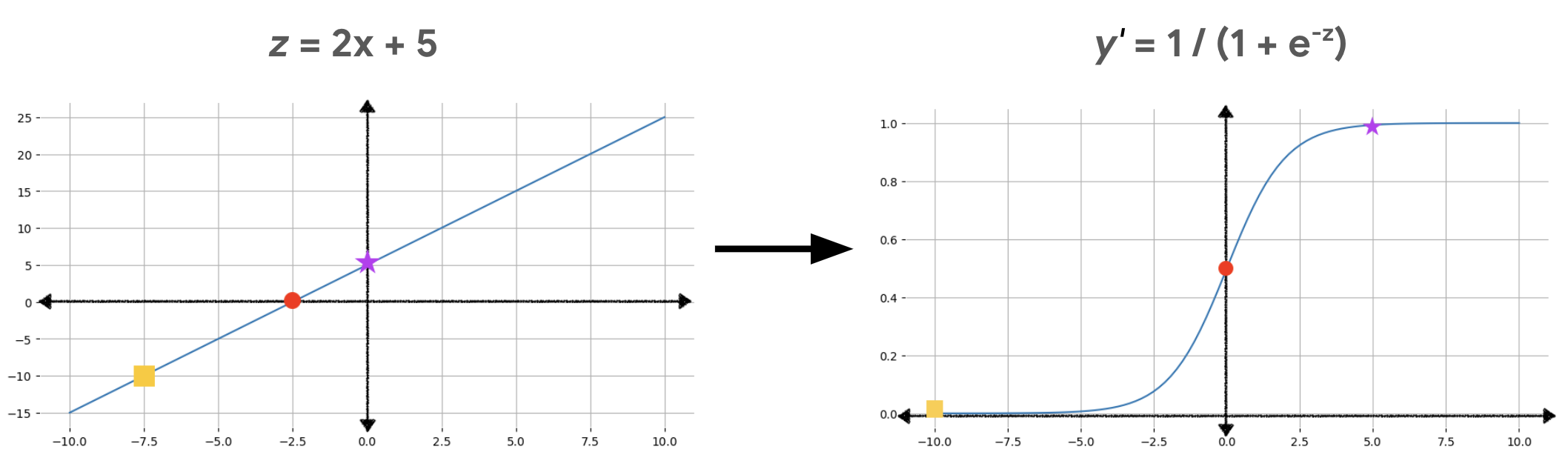
Na rysunku 2 równanie liniowe jest daną wejściową funkcji sigmoidalnej, która przekształca linię prostą w kształt litery S. Zwróć uwagę, że równanie liniowe może zwracać bardzo duże lub bardzo małe wartości z, ale wynik funkcji sigmoidalnej y' zawsze mieści się w zakresie od 0 do 1 (bez wartości granicznych). Na przykład żółty kwadrat na wykresie po lewej stronie ma wartość z równą –10, ale funkcja sigmoid na wykresie po prawej stronie mapuje tę wartość na y' = 0, 00004.

Ćwiczenie: sprawdź swoją wiedzę

Model regresji logistycznej z 3 cechami ma te odchylenia i wagi:

\[\begin{align} b &= 1 \\ w_1 &= 2 \\ w_2 &= -1 \\ w_3 &= 5 \end{align} \]

Biorąc pod uwagę te wartości wejściowe:

\[\begin{align} x_1 &= 0 \\ x_2 &= 10 \\ x_3 &= 2 \end{align} \]

Odpowiedz na te 2 pytania.

1. Jaka jest wartość z dla tych wartości wejściowych?

–1

0

0,731

1

Dobrze! Równanie liniowe zdefiniowane przez wagi i wyraz wolny to z = 1 + 2x₁ – x₂ + 5x₃. Po wstawieniu wartości wejściowych do równania otrzymujemy z = 1 + (2)(0) – (10) + (5)(2) = 1.

2. Jaka jest prognoza regresji logistycznej dla tych wartości wejściowych?

0.268

0,5

0,731

Jak obliczyliśmy w punkcie 1 powyżej, logit dla wartości wejściowych wynosi 1. Podstawiając tę wartość za z do funkcji sigmoidalnej:

\(y = \frac{1}{1 + e^{-z}} = \frac{1}{1 + e^{-1}} = \frac{1}{1 + 0.367} = \frac{1}{1.367} = 0.731\)

1

Pamiętaj, że wynik funkcji sigmoid będzie zawsze większy od 0 i mniejszy od 1.

Kluczowe terminy:

• Klasyfikacja binarna
• Logarytm szans
• Regresja logistyczna
• Funkcja sigmoid