Birçok problemde çıktı olarak olasılık tahmini gerekir. Mantıksal regresyon, olasılıkları hesaplamak için son derece verimli bir mekanizmadır. Pratik olarak, döndürülen olasılığı aşağıdaki iki şekilde kullanabilirsiniz:
"Olduğu gibi" uygulanır. Örneğin, bir spam tahmini modeli e-postayı giriş olarak alıp
0.932değerini çıkış olarak veriyorsa bu, e-postanın spam olma olasılığının93.2%olduğu anlamına gelir.TrueveyaFalse,SpamveyaNot Spamgibi ikili bir kategoriye dönüştürülür.
Bu modülde, lojistik regresyon modeli çıkışını olduğu gibi kullanmaya odaklanılmaktadır. Sınıflandırma modülünde bu çıkışı ikili bir kategoriye dönüştürmeyi öğreneceksiniz.
Sigmoid işlevi
Mantıksal regresyon modelinin, çıktısının her zaman 0 ile 1 arasında bir değer vererek olasılığı temsil etmesini nasıl sağladığını merak ediyor olabilirsiniz. Bu özelliklere sahip bir çıktı veren lojistik fonksiyonlar adı verilen bir fonksiyon ailesi vardır. Sigmoid fonksiyonu olarak da bilinen standart lojistik fonksiyonun (sigmoid, "S şeklinde" anlamına gelir) formülü şöyledir:
\[f(x) = \frac{1}{1 + e^{-x}}\]
Bu örnekte:
- f(x), sigmoid fonksiyonunun çıkışıdır.
- e, Euler sayısıdır: ≈ 2,71828 olan matematiksel bir sabittir.
- x, sigmoid işlevinin girdisidir.
Şekil 1'de sigmoid fonksiyonunun ilgili grafiği gösterilmektedir.
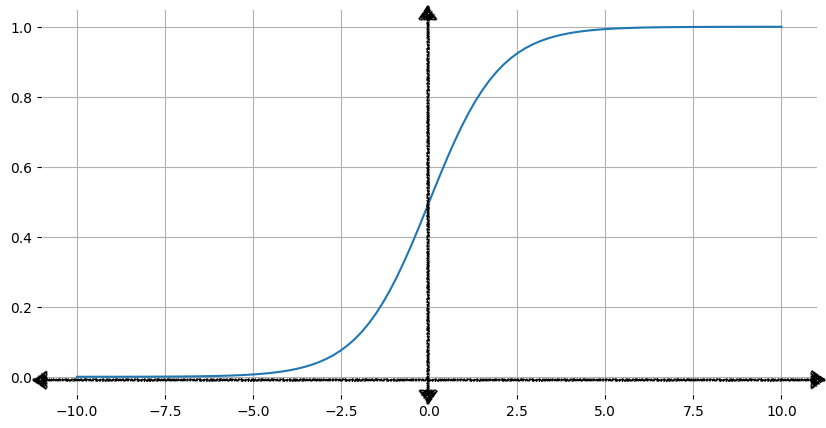
Giriş x arttıkça sigmoid fonksiyonunun çıkışı 1 değerine yaklaşır ancak asla ulaşmaz. Benzer şekilde, giriş azaldıkça sigmoid fonksiyonunun çıktısı 0 değerine yaklaşır ancak asla ulaşmaz.
Sigmoid fonksiyonunun arkasındaki matematik hakkında daha ayrıntılı bilgi için burayı tıklayın.
Aşağıdaki tabloda, -7 ile 7 arasındaki giriş değerleri için sigmoid fonksiyonunun çıkış değerleri gösterilmektedir. Sigmoid fonksiyonunun, azalan negatif giriş değerleri için 0'a, artan pozitif giriş değerleri için ise 1'e ne kadar hızlı yaklaştığına dikkat edin.
Ancak giriş değeri ne kadar büyük veya küçük olursa olsun çıkış her zaman 0'dan büyük ve 1'den küçük olur.
| Giriş | Sigmoid çıkışı |
|---|---|
| -7 | 0,001 |
| -6 | 0,002 |
| -5 | 0,007 |
| -4 | 0,018 |
| -3 | 0,047 |
| -2 | 0,119 |
| -1 | 0,269 |
| 0 | 0,50 |
| 1 | 0,731 |
| 2 | 0,881 |
| 3 | 0,952 |
| 4 | 0,982 |
| 5 | 0,993 |
| 6 | 0,997 |
| 7 | 0,999 |
Sigmoid fonksiyonunu kullanarak doğrusal çıkışı dönüştürme
Aşağıdaki denklem, lojistik regresyon modelinin doğrusal bileşenini temsil eder:
\[z = b + w_1x_1 + w_2x_2 + \ldots + w_Nx_N\]
Bu örnekte:
- z, doğrusal denklemin sonucudur ve log odds olarak da adlandırılır.
- b, yanlılığı ifade eder.
- w değerleri, modelin öğrendiği ağırlıklardır.
- x değerleri, belirli bir örneğin özellik değerleridir.
Mantıksal regresyon tahminini elde etmek için z değeri sigmoid işlevine iletilir. Bu işlev, 0 ile 1 arasında bir değer (olasılık) döndürür:
\[y' = \frac{1}{1 + e^{-z}}\]
Bu örnekte:
- y, mantıksal regresyon modelinin çıkışıdır.
- e, Euler sayısıdır: ≈ 2,71828 olan matematiksel bir sabittir.
- z, doğrusal çıkıştır (önceki denklemde hesaplandığı gibi).
Log-odds hakkında daha fazla bilgi edinmek için burayı tıklayın.
$z = b + w_1x_1 + w_2x_2 + \ldots + w_Nx_N$ denkleminde z, log-odds olarak adlandırılır. Bunun nedeni, aşağıdaki sigmoid işleviyle (burada $y$, olasılığı temsil eden bir lojistik regresyon modelinin çıkışıdır) başlamanız durumunda:
$$y = \frac{1}{1 + e^{-z}}$$
Ardından z'yi bulun:
$$ z = \ln\left(\frac{y}{1-y}\right) $$
Ardından z, iki olası sonucun (y ve 1 – y) olasılık oranının doğal logaritması olarak tanımlanır.
Şekil 2'de, bu hesaplamalar kullanılarak doğrusal çıkışın lojistik regresyon çıkışına nasıl dönüştürüldüğü gösterilmektedir.
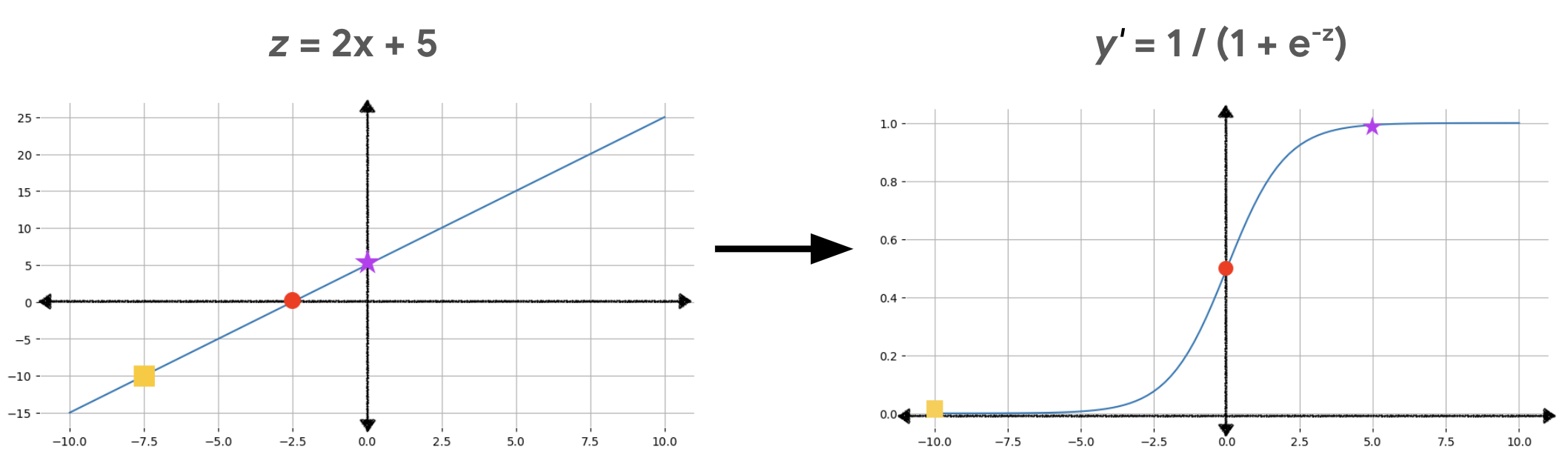
Şekil 2'de, doğrusal bir denklem, doğru çizgiyi s şekline büken sigmoid fonksiyonuna giriş olur. Doğrusal denklemin z'nin çok büyük veya çok küçük değerlerini verebileceğini, ancak sigmoid fonksiyonunun çıktısı olan y'nin her zaman 0 ile 1 arasında (sınırlar hariç) olduğunu unutmayın. Örneğin, soldaki grafikteki sarı karenin z değeri -10'dur ancak sağdaki grafikteki sigmoid işlevi bu -10 değerini 0, 00004 y' değerine eşler.
Alıştırma: Anlayıp anlamadığınızı kontrol edin
Üç özellikli bir lojistik regresyon modelinin aşağıdaki sapması ve ağırlıkları vardır:
\[\begin{align} b &= 1 \\ w_1 &= 2 \\ w_2 &= -1 \\ w_3 &= 5 \end{align} \]
Aşağıdaki giriş değerleri verildiğinde:
\[\begin{align} x_1 &= 0 \\ x_2 &= 10 \\ x_3 &= 2 \end{align} \]
Aşağıdaki iki soruyu yanıtlayın.
Yukarıdaki 1. adımda hesaplandığı gibi, giriş değerlerinin log-odds'u 1'dir. z değeri için bu değeri sigmoid işlevine yerleştirin:
\(y = \frac{1}{1 + e^{-z}} = \frac{1}{1 + e^{-1}} = \frac{1}{1 + 0.367} = \frac{1}{1.367} = 0.731\)