許多問題都需要以機率估算值做為輸出內容。 邏輯迴歸是計算機率的極有效率機制。實務上,您可以透過下列任一方式使用傳回的機率:
「照原樣」套用。舉例來說,如果垃圾內容預測模型將電子郵件做為輸入內容,並輸出
0.932值,這表示電子郵件是垃圾內容的機率為93.2%。轉換為二元類別,例如
True或False、Spam或Not Spam。
本單元著重於直接使用邏輯迴歸模型輸出內容。在分類單元中,您將瞭解如何將這項輸出內容轉換為二元類別。
Sigmoid 函數
您可能想知道,邏輯迴歸模型如何確保輸出結果代表機率,且一律輸出介於 0 和 1 之間的值。巧合的是,有一系列函式稱為「邏輯函式」,其輸出內容具有相同的特徵。標準邏輯函式又稱「S 函數」 (「S 函數」sigmoid意指「S 形」),公式如下:
\[f(x) = \frac{1}{1 + e^{-x}}\]
其中:
- f(x) 是 sigmoid 函式的輸出內容。
- e 是歐拉數: 數學常數 ≈ 2.71828。
- x 是 S 函數的輸入值。
圖 1 顯示對應的 Sigmoid 函式圖。
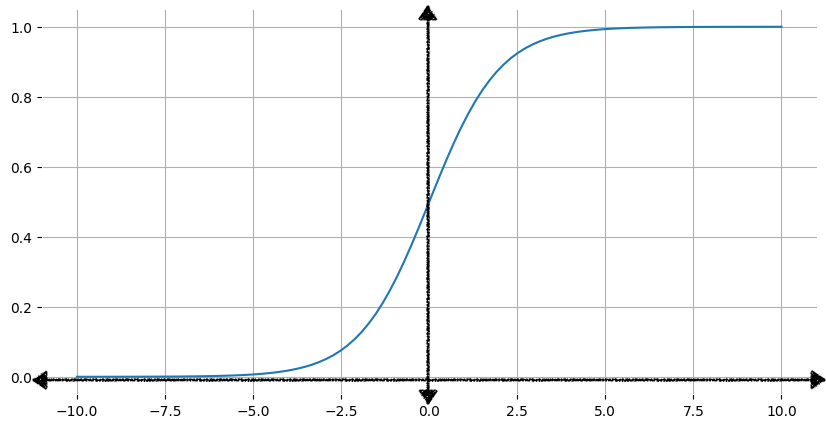
隨著輸入 x 增加,Sigmoid 函式的輸出會趨近於 1,但永遠不會達到 1。同樣地,輸入值越小,Sigmoid 函式的輸出值就越接近 0,但永遠不會達到 0。
按這裡深入瞭解 Sigmoid 函式背後的數學原理
下表顯示輸入值介於 -7 到 7 之間時,Sigmoid 函式的輸出值。請注意,隨著負輸入值減少,S 型函數會迅速趨近於 0;隨著正輸入值增加,S 型函數會迅速趨近於 1。
不過,無論輸入值多大或多小,輸出值一律會大於 0 且小於 1。
| 輸入 | Sigmoid 輸出 |
|---|---|
| -7 | 0.001 |
| -6 | 0.002 |
| -5 | 0.007 |
| -4 | 0.018 |
| -3 | 0.047 |
| -2 | 0.119 |
| -1 | 0.269 |
| 0 | 0.50 |
| 1 | 0.731 |
| 2 | 0.881 |
| 3 | 0.952 |
| 4 | 0.982 |
| 5 | 0.993 |
| 6 | 0.997 |
| 7 | 0.999 |
使用 Sigmoid 函式轉換線性輸出
下列方程式代表羅吉斯迴歸模型的線性成分:
\[z = b + w_1x_1 + w_2x_2 + \ldots + w_Nx_N\]
其中:
- z 是線性方程式的輸出內容,也稱為對數勝算。
- b 是偏誤。
- w 值是模型學習到的權重。
- x 值是特定範例的特徵值。
如要取得邏輯迴歸預測結果,請將 z 值傳遞至 S 函數,產生介於 0 和 1 之間的值 (機率):
\[y' = \frac{1}{1 + e^{-z}}\]
其中:
- y' 是邏輯迴歸模型的輸出內容。
- e 是歐拉數: 數學常數 ≈ 2.71828。
- z 是線性輸出 (如上述方程式所計算)。
按這裡進一步瞭解對數比
在方程式 $z = b + w_1x_1 + w_2x_2 + \ldots + w_Nx_N$ 中,z 稱為對數勝算,因為如果您從下列 Sigmoid 函式開始 (其中 $y$ 是邏輯迴歸模型的輸出,代表機率):
$$y = \frac{1}{1 + e^{-z}}$$
然後求解 z:
$$ z = \ln\left(\frac{y}{1-y}\right) $$
接著,z 定義為兩種可能結果 (y 和 1 – y) 機率比率的自然對數。
圖 2 說明如何使用這些計算,將線性輸出轉換為邏輯迴歸輸出。
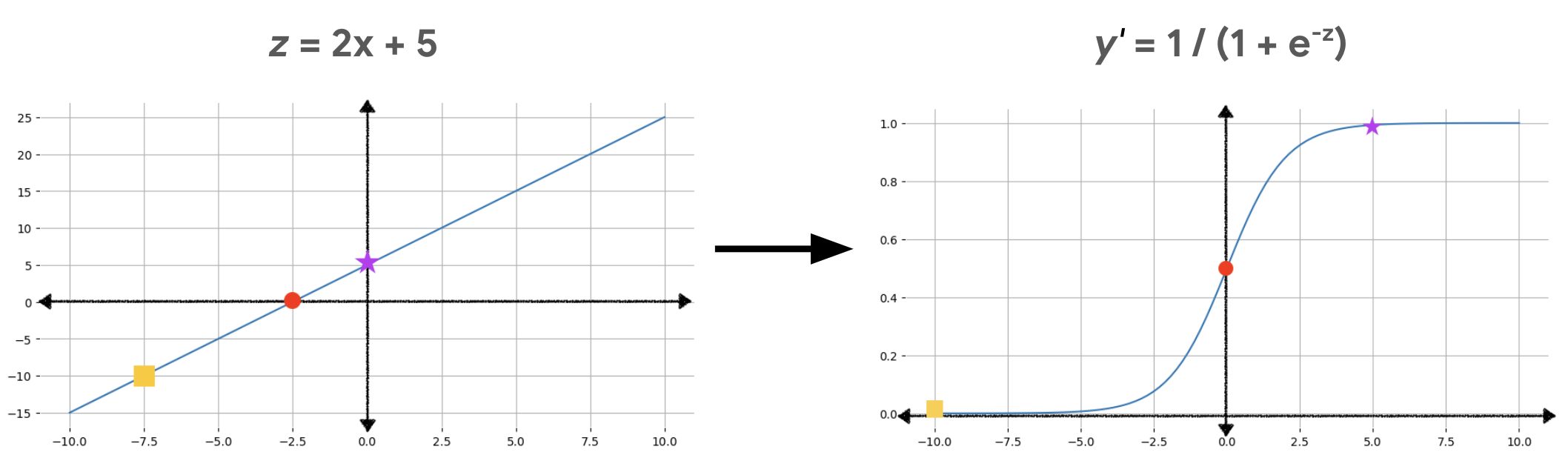
如圖 2 所示,線性方程式會成為 S 函數的輸入,請注意,線性方程式可以輸出非常大或非常小的 z 值,但 Sigmoid 函式的輸出值 y' 一律介於 0 和 1 之間 (不含 0 和 1)。舉例來說,左側圖表中的黃色正方形 z 值為 -10,但右側圖表中的 Sigmoid 函式會將 -10 對應至 y' 值 0.00004。
練習:確認理解程度
具有三項特徵的邏輯迴歸模型具有下列偏差和權重:
\[\begin{align} b &= 1 \\ w_1 &= 2 \\ w_2 &= -1 \\ w_3 &= 5 \end{align} \]
假設有下列輸入值:
\[\begin{align} x_1 &= 0 \\ x_2 &= 10 \\ x_3 &= 2 \end{align} \]
請回答下列兩個問題。
如上述 #1 計算結果,輸入值的對數勝算為 1。 將 z 的值代入 Sigmoid 函式:
\(y = \frac{1}{1 + e^{-z}} = \frac{1}{1 + e^{-1}} = \frac{1}{1 + 0.367} = \frac{1}{1.367} = 0.731\)
