Nhiều bài toán yêu cầu kết quả ước tính xác suất. Hồi quy logistic là một cơ chế cực kỳ hiệu quả để tính xác suất. Về mặt thực tế, bạn có thể sử dụng xác suất được trả về theo một trong hai cách sau:
Áp dụng "nguyên trạng". Ví dụ: nếu một mô hình dự đoán thư rác lấy email làm giá trị đầu vào và xuất ra giá trị
0.932, thì điều này có nghĩa là email có xác suất93.2%là thư rác.Đã chuyển đổi thành danh mục nhị phân chẳng hạn như
TruehoặcFalse,SpamhoặcNot Spam.
Mô-đun này tập trung vào việc sử dụng đầu ra của mô hình hồi quy logistic. Trong Mô-đun Phân loại, bạn sẽ tìm hiểu cách chuyển đổi dữ liệu đầu ra này thành một danh mục nhị phân.
Hàm sigmoid
Bạn có thể thắc mắc làm cách nào để mô hình hồi quy logistic có thể đảm bảo đầu ra của mô hình đại diện cho một xác suất, luôn xuất ra một giá trị từ 0 đến 1. Như vậy xảy ra, có một nhóm hàm được gọi là hàm logistic có đầu ra có cùng đặc điểm đó. Hàm logistic chuẩn, còn được gọi là hàm sigmoid (sigmoid có nghĩa là "hình chữ s"), có công thức:
\[f(x) = \frac{1}{1 + e^{-x}}\]
Hình 1 cho thấy biểu đồ tương ứng của hàm sigmoid.
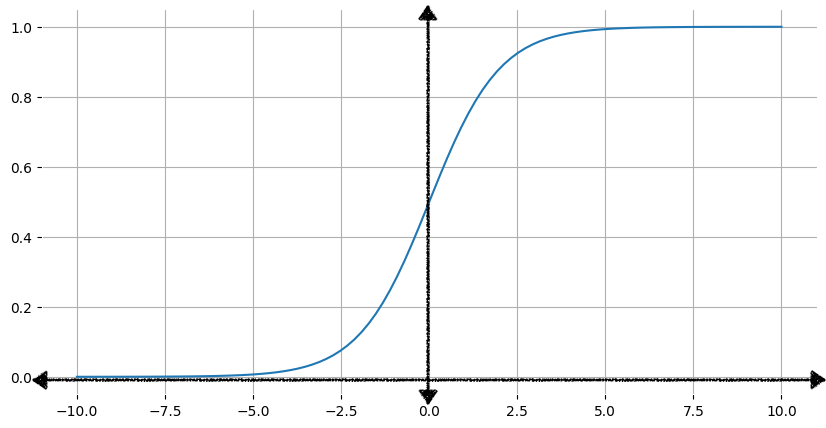
Khi dữ liệu đầu vào, x, tăng lên, đầu ra của hàm sigmoid sẽ tiến gần nhưng không bao giờ đạt đến 1. Tương tự, khi đầu vào giảm, đầu ra của hàm sigmoid sẽ tiến gần nhưng không bao giờ đạt đến 0.
Nhấp vào đây để tìm hiểu sâu hơn về toán học đằng sau hàm sigmoid
Bảng dưới đây cho thấy các giá trị đầu ra của hàm sigmoid cho các giá trị đầu vào trong phạm vi –7 đến 7. Chú ý tốc độ đến gần của sigmoid 0 để giảm giá trị đầu vào âm và tốc độ tiếp cận sigmoid 1 để tăng giá trị đầu vào dương.
Tuy nhiên, bất kể giá trị đầu vào lớn hay nhỏ, đầu ra sẽ luôn lớn hơn 0 và nhỏ hơn 1.
| Đầu vào | Đầu ra Sigmoid |
|---|---|
| -7 | 0,001 |
| -6 | 0,002 |
| -5 | 0,007 |
| -4 | 0,018 |
| -3 | 0,047 |
| -2 | 0,119 |
| -1 | 0,269 |
| 0 | 0,5 |
| 1 | 0,731 |
| 2 | 0,881 |
| 3 | 0,952 |
| 4 | 0,982 |
| 5 | 0,993 |
| 6 | 0,997 |
| 7 | 0,999 |
Biến đổi đầu ra tuyến tính bằng hàm sigmoid
Phương trình sau đây biểu diễn thành phần tuyến tính của một lôgarit mô hình hồi quy:
\[z = b + w_1x_1 + w_2x_2 + \ldots + w_Nx_N\]
trong đó:
- z là kết quả của phương trình tuyến tính, còn gọi là tỷ lệ log.
- b là độ lệch.
- Giá trị w là các trọng số đã học của mô hình.
- Các giá trị x là giá trị đặc điểm cho một ví dụ cụ thể.
Để có được dự đoán hồi quy logit, giá trị z sau đó được chuyển đến hàm sigmoid, mang lại giá trị (xác suất) trong khoảng từ 0 đến 1:
\[y' = \frac{1}{1 + e^{-z}}\]
trong đó:
- y' là kết quả của mô hình hồi quy logistic.
- z là đầu ra tuyến tính (như được tính trong phương trình trước đó).
Nhấp vào đây để tìm hiểu thêm về tỷ lệ chênh lệch nhật ký
Trong phương trình $z = b + w_1x_1 + w_2x_2 + \ldots + w_Nx_N$, z được gọi là tỷ lệ chênh lệch nhật ký vì nếu bạn bắt đầu bằng hàm sigmoid sau (trong đó $y$ là kết quả của một hàm logistic mô hình hồi quy, biểu thị một xác suất):
$$y = \frac{1}{1 + e^{-z}}$$
Sau đó, giải phương trình cho z:
$$ z = \log\left(\frac{y}{1-y}\right) $$
Khi đó z được định nghĩa là log của tỷ lệ các xác suất trong hai kết quả có thể xảy ra là: y và 1 – y.
Hình 2 minh hoạ cách đầu ra tuyến tính được chuyển đổi thành đầu ra hồi quy logistic bằng cách sử dụng các phép tính này.
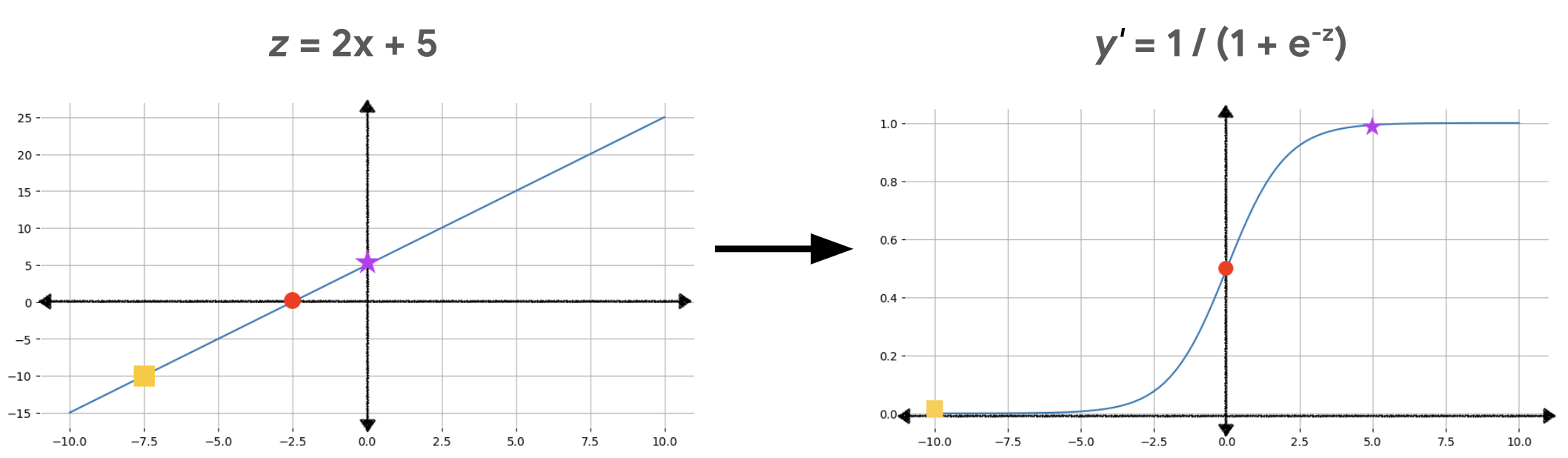
Trong Hình 2, một phương trình tuyến tính trở thành dữ liệu đầu vào cho hàm sigmoid, hàm này sẽ bẻ cong đường thẳng thành hình chữ S. Lưu ý rằng phương trình tuyến tính có thể cho ra các giá trị z rất lớn hoặc rất nhỏ, nhưng đầu ra của sigmoid hàm y', luôn nằm trong khoảng từ 0 đến 1 và không bao gồm 0 và 1. Ví dụ: màu vàng hình vuông trên đồ thị bên trái có giá trị z là –10, nhưng hàm sigmoid trong đồ thị bên phải ánh xạ –10 thành y' giá trị 0,00004.
Bài tập: Kiểm tra kiến thức
Mô hình hồi quy logistic có ba đặc điểm có độ lệch và trọng số sau:
\[\begin{align} b &= 1 \\ w_1 &= 2 \\ w_2 &= -1 \\ w_3 &= 5 \end{align} \]
Cho các giá trị đầu vào sau:
\[\begin{align} x_1 &= 0 \\ x_2 &= 10 \\ x_3 &= 2 \end{align} \]
Hãy trả lời hai câu hỏi sau đây.
Như đã tính toán trong phần 1 ở trên, số lẻ log cho các giá trị đầu vào là 1. Cắm giá trị đó cho z vào hàm sigmoid:
\(y = \frac{1}{1 + e^{-z}} = \frac{1}{1 + e^{-1}} = \frac{1}{1 + 0.367} = \frac{1}{1.367} = 0.731\)