많은 문제에 확률 추정치가 출력으로 필요합니다. 로지스틱 회귀는 매우 효율적인 확률 계산 메커니즘입니다. 실제로 반환된 확률을 다음 두 방법 중 하나로 사용할 수 있습니다.
'그대로' 적용. 예를 들어 스팸 예측 모델에서 이메일을 입력으로 사용하고
0.932값을 출력한다면, 이는 이메일이 스팸일 확률이93.2%임을 의미합니다.바이너리 카테고리로 변환(예:
True또는False,Spam또는Not Spam)
이 모듈에서는 로지스틱 회귀 모델 출력을 그대로 사용하는 것에 중점을 둡니다. 분류 모듈에서는 이 출력을 바이너리 카테고리로 변환하는 방법을 알아봅니다.
시그모이드 함수
로지스틱 회귀 모델에서 어떻게 출력이 확률을 나타내고 항상 0과 1 사이의 값을 출력할 수 있는지 궁금할 수 있습니다. 마침 로지스틱 함수라는 함수 계열이 있는데 이 함수의 출력에 동일한 특성이 있습니다. 표준 로지스틱 함수(시그모이드 함수라고도 하며 시그모이드는 's자 모양'을 의미함)의 수식은 다음과 같습니다.
\[f(x) = \frac{1}{1 + e^{-x}}\]
그림 1은 이에 상응하는 시그모이드 함수의 그래프를 보여줍니다.
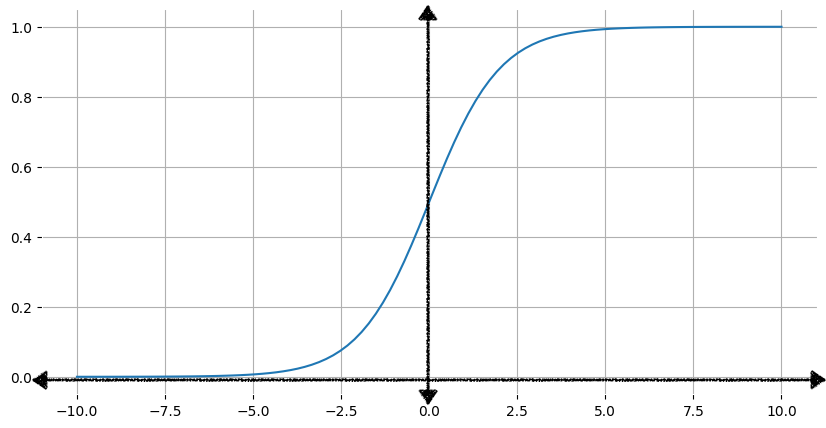
입력값 x가 증가할수록 시그모이드 함수의 출력값은 1에 가까워지지만, 도달하지는 않습니다. 마찬가지로 입력값이 감소할수록 시그모이드 함수의 출력값은 0에 가까워지지만 도달하지는 않습니다.
여기를 클릭하여 시그모이드 함수의 수학에 관해 자세히 알아보기
아래 표는 -7~7 범위의 입력값에 대한 시그모이드 함수의 출력값을 보여줍니다. 음의 입력값이 감소할 때 시그모이드가 0에 얼마나 빨리 가까워지는지, 양의 입력값이 증가할 때 시그모이드가 얼마나 빨리 1에 가까워지는지 확인해 보세요.
하지만 입력값이 크든 작든 출력값은 항상 0보다 크고 1보다 작습니다.
| 입력 | 시그모이드 출력 |
|---|---|
| -7 | 0.001 |
| -6 | 0.002 |
| -5 | 0.007 |
| -4 | 0.018 |
| -3 | 0.047 |
| -2 | 0.119 |
| -1 | 0.269 |
| 0 | 0.50 |
| 1 | 0.731 |
| 2 | 0.881 |
| 3 | 0.952 |
| 4 | 0.982 |
| 5 | 0.993 |
| 6 | 0.997 |
| 7 | 0.999 |
시그모이드 함수를 사용하여 선형 출력 변환하기
다음 방정식은 로지스틱 회귀 모델의 선형 구성요소를 나타냅니다.
\[z = b + w_1x_1 + w_2x_2 + \ldots + w_Nx_N\]
각 항목의 의미는 다음과 같습니다.
- z는 선형 방정식의 출력으로, 로그 오즈라고도 합니다.
- b는 편향입니다.
- w값은 모델의 학습된 가중치입니다.
- x값은 특정 예에 대한 특성값입니다.
로지스틱 회귀 예측을 얻기 위해 다음과 같이 z값이 시그모이드 함수로 전달되어 0과 1 사이의 값(확률)이 생성됩니다.
\[y' = \frac{1}{1 + e^{-z}}\]
각 항목의 의미는 다음과 같습니다.
- y'는 로지스틱 회귀 모델의 출력입니다.
- z는 선형 출력입니다(위 방정식에서 계산됨).
여기를 클릭하여 로그 오즈에 대해 자세히 알아보기
$z = b + w_1x_1 + w_2x_2 + \ldots + w_Nx_N$ 방정식에서 z는 로그 오즈라고 합니다. 아래 시그모이드 함수(여기서 $y$는 로지스틱 회귀 모델의 출력이며 확률을 나타냄)로 시작하기 때문입니다.
$$y = \frac{1}{1 + e^{-z}}$$
그런 다음 z를 구합니다.
$$ z = \log\left(\frac{y}{1-y}\right) $$
그러면 z는 두 가지 가능한 결과인 y와 1 – y의 확률 비율의 로그로 정의됩니다.
그림 2는 다음 계산을 사용하여 선형 출력이 로지스틱 회귀 출력으로 변환되는 방식을 보여줍니다.
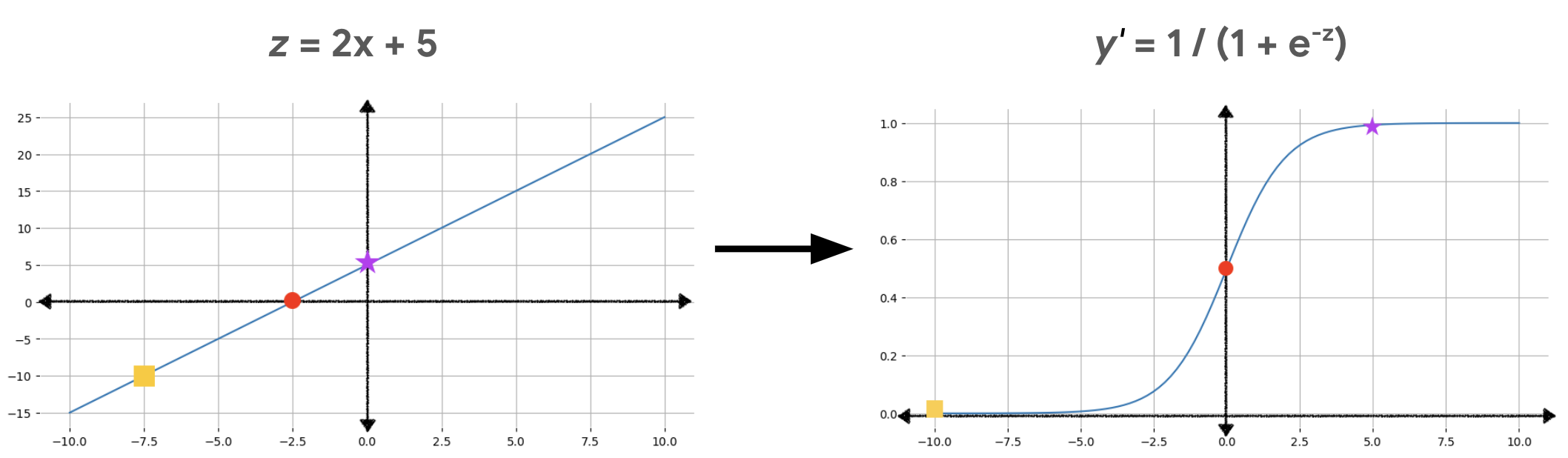
그림 2에서 선형 방정식은 시그모이드 함수의 입력이 되므로 직선이 s자 모양으로 구부러집니다. 선형 방정식은 매우 크거나 매우 작은 z값을 출력할 수 있지만, 시그모이드 함수 출력인 y'는 항상 0보다 크고 1보다 작은 값입니다. 예를 들어 왼쪽 그래프의 노란색 사각형은 z값이 –10이지만 오른쪽 그래프의 시그모이드 함수에서는 –10을 0.00004라는 y'값에 매핑합니다.
연습: 학습 내용 점검하기
세 가지 특성이 있는 로지스틱 회귀 모델의 편향과 가중치는 다음과 같습니다.
\[\begin{align} b &= 1 \\ w_1 &= 2 \\ w_2 &= -1 \\ w_3 &= 5 \end{align} \]
입력값은 다음과 같습니다.
\[\begin{align} x_1 &= 0 \\ x_2 &= 10 \\ x_3 &= 2 \end{align} \]
다음 두 질문에 답하세요.
위의 1번 질문에서 계산했듯이 입력값의 로그 오즈는 1입니다. z의 이 값을 시그모이드 함수에 대입하면 다음과 같습니다.
\(y = \frac{1}{1 + e^{-z}} = \frac{1}{1 + e^{-1}} = \frac{1}{1 + 0.367} = \frac{1}{1.367} = 0.731\)