Muchos problemas requieren una estimación de probabilidad como resultado. La regresión logística es un mecanismo extremadamente eficiente para calcular probabilidades. En términos prácticos, puedes usar la probabilidad que se muestra de las siguientes dos maneras:
Se aplica "tal cual". Por ejemplo, si un modelo de predicción de spam toma un correo electrónico como entrada y muestra un valor de
0.932, esto implica una probabilidad de93.2%de que el correo electrónico sea spam.Se convirtió en una categoría binaria. como
TrueoFalse,SpamoNot Spam.
En este módulo, se enfoca en usar el resultado del modelo de regresión logística tal como está. En el módulo de clasificación, aprenderás a convertir este resultado en una categoría binaria.
Función sigmoidea
Quizá te preguntes cómo un modelo de regresión logística puede garantizar representa una probabilidad, siempre da como resultado un valor entre 0 y 1. Como suele pasar, hay una familia de funciones llamadas funciones logísticas cuyo resultado tiene esas mismas características. La función logística estándar, también conocida como función sigmoidea (sigmoidea significa "en forma de S"), tiene la siguiente fórmula:
\[f(x) = \frac{1}{1 + e^{-x}}\]
En la Figura 1, se muestra el gráfico correspondiente de la función sigmoidea.
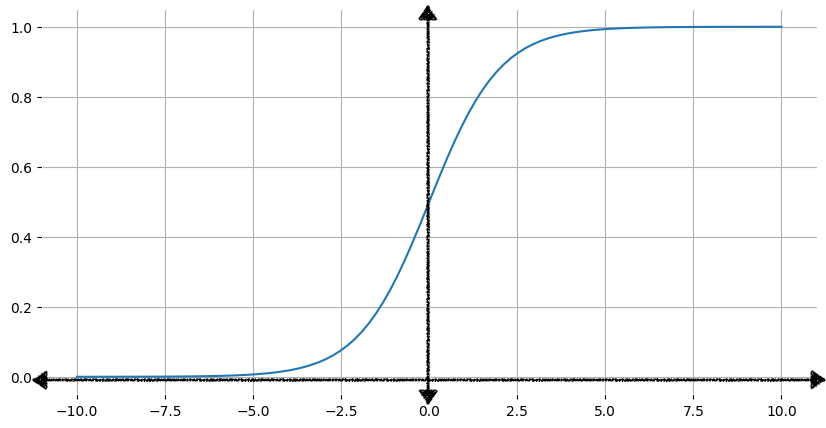
A medida que aumenta la entrada, x, el resultado de la función sigmoidea se acerca a
pero nunca llega a 1. De manera similar, a medida que disminuye la entrada, la capa
se aproxima la salida de la función, pero nunca alcanza 0.
Haz clic aquí para obtener más información sobre las matemáticas detrás de la función sigmoidea
La tabla a continuación muestra los valores de salida de la función sigmoidea para valores de entrada en el rango de –7 a 7. Observa la rapidez con la que la función sigmoidea se aproxima a 0 para disminuir los valores de entrada negativos y la rapidez con la que se aproxima a 1 para aumentar los valores de entrada positivos.
Sin embargo, independientemente de lo grande o pequeño que sea el valor de entrada, el resultado siempre será mayor que 0 y menor que 1.
| Entrada | Salida sigmoidea |
|---|---|
| -7 | 0.001 |
| -6 | 0.002 |
| -5 | 0.007 |
| -4 | 0.018 |
| -3 | 0.047 |
| -2 | 0.119 |
| -1 | 0.269 |
| 0 | 0.50 |
| 1 | 0,731 |
| 2 | 0.881 |
| 3 | 0.952 |
| 4 | 0.982 |
| 5 | 0.993 |
| 6 | 0,997 |
| 7 | 0.999 |
Transformación de resultados lineales con la función sigmoidea
La siguiente ecuación representa el componente lineal de una logística de regresión:
\[z = b + w_1x_1 + w_2x_2 + \ldots + w_Nx_N\]
Donde:
- z es el resultado de la ecuación lineal, también llamada odds logarítmicas.
- b es el sesgo.
- Los valores w son los pesos aprendidos del modelo.
- Los valores x son los valores de atributo para un ejemplo en particular.
Para obtener la predicción de la regresión logística, el valor z se pasa a la función sigmoidea, lo que genera un valor (una probabilidad) entre 0 y 1:
\[y' = \frac{1}{1 + e^{-z}}\]
Donde:
- y' es el resultado del modelo de regresión logística.
- z es el resultado lineal (como se calcula en la ecuación anterior).
Haz clic aquí para obtener más información sobre las log-odds
En la ecuación $z = b + w_1x_1 + w_2x_2 + \ldots + w_Nx_N$, z se conoce como logaritmo de probabilidad porque si comienzas siguiente función sigmoidea (donde $y$ es la salida de una de regresión, que representa una probabilidad):
$$y = \frac{1}{1 + e^{-z}}$$
Luego, resuelve z:
$$ z = \log\left(\frac{y}{1-y}\right) $$
Luego, z se define como el registro de la proporción de las probabilidades de los dos resultados posibles: y y 1 – y.
En la Figura 2, se ilustra cómo se transforma el resultado lineal en el resultado de la regresión logística con estos cálculos.
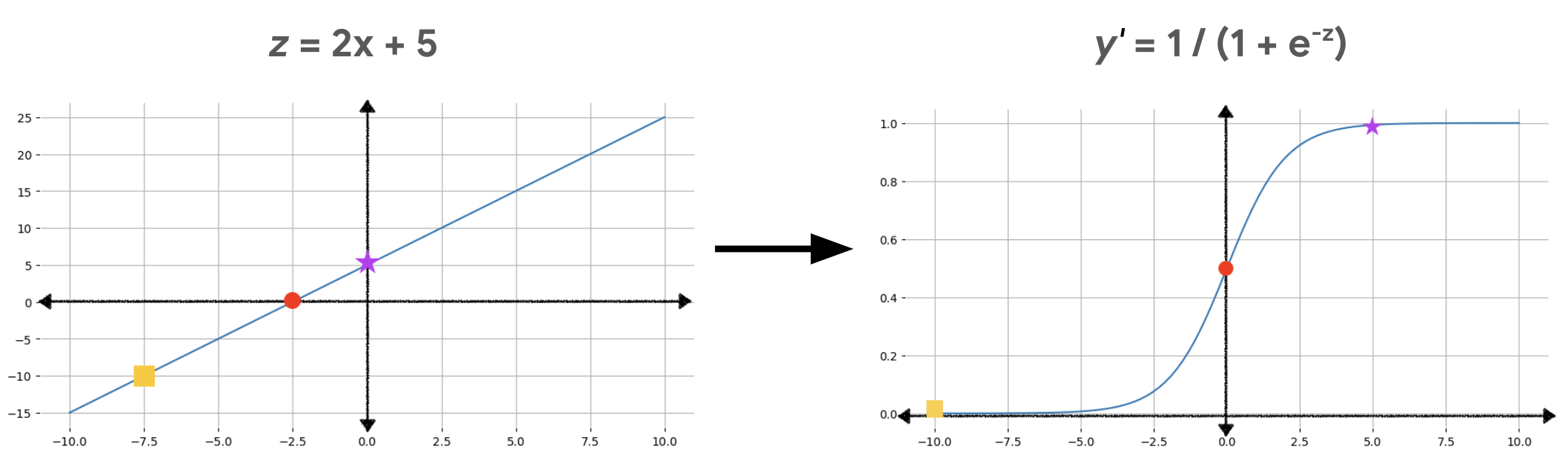
En la Figura 2, una ecuación lineal se convierte en la entrada de la función sigmoidea, que dobla la línea recta en forma de S. Observa que la ecuación lineal puede generar valores de z muy grandes o muy pequeños, pero la salida de la “y” siempre está entre 0 y 1, exclusivo. Por ejemplo, el color amarillo cuadrado en el gráfico de la izquierda tiene un valor z de –10, pero la función sigmoidea en la gráfico derecho mapea eso -10 en una Y' de 0.00004.
Ejercicio: Comprueba tu comprensión
Un modelo de regresión logística con tres atributos tiene los siguientes pesos y polarizaciones:
\[\begin{align} b &= 1 \\ w_1 &= 2 \\ w_2 &= -1 \\ w_3 &= 5 \end{align} \]
Dadas las siguientes entradas:
\[\begin{align} x_1 &= 0 \\ x_2 &= 10 \\ x_3 &= 2 \end{align} \]
Responde estas dos preguntas.
Como se calculó en el paso 1, el logaritmo de probabilidad para los valores de entrada es 1. Cuando insertas ese valor para z en la función sigmoidea, sucede lo siguiente:
\(y = \frac{1}{1 + e^{-z}} = \frac{1}{1 + e^{-1}} = \frac{1}{1 + 0.367} = \frac{1}{1.367} = 0.731\)