Regressione logistica: calcolare una probabilità con la funzione sigmoidea

Molti problemi richiedono una stima di probabilità come output. La regressione logistica è un meccanismo estremamente efficiente per calcolare le probabilità. In pratica puoi usare la probabilità restituita in uno dei seguenti modi in due modi:

• Applicate "così come sono". Ad esempio, se un modello di previsione dello spam prende un'email come input e restituisce un valore 0.932, ciò implica una probabilità di 93.2% che l'email sia spam.

• Transazione convertita in una categoria binaria come True o False, Spam o Not Spam.

Questo modulo si concentra sull'utilizzo dell'output del modello di regressione logistica così com'è. Nel modulo Classificazione, imparerai a convertire questo output in una categoria binaria.

Funzione sigmoidea

Forse ti starai chiedendo in che modo un modello di regressione logistica può garantire rappresenta una probabilità, producendo sempre un valore compreso tra 0 e 1. Esiste infatti una famiglia di funzioni chiamate funzioni logistiche il cui output presenta le stesse caratteristiche. La funzione logistica standard, chiamata anche funzione sigmoidea (sigmoidea significa "a forma di S"), ha la formula:

\[f(x) = \frac{1}{1 + e^{-x}}\]

La Figura 1 mostra il grafico corrispondente della funzione sigmoidea.

Figura 1. Grafico della funzione sigmoidea. La curva si avvicina a 0 quando i valori di x diminuiscono fino a infinito negativo e a 1 quando i valori di x aumentano verso l'infinito.

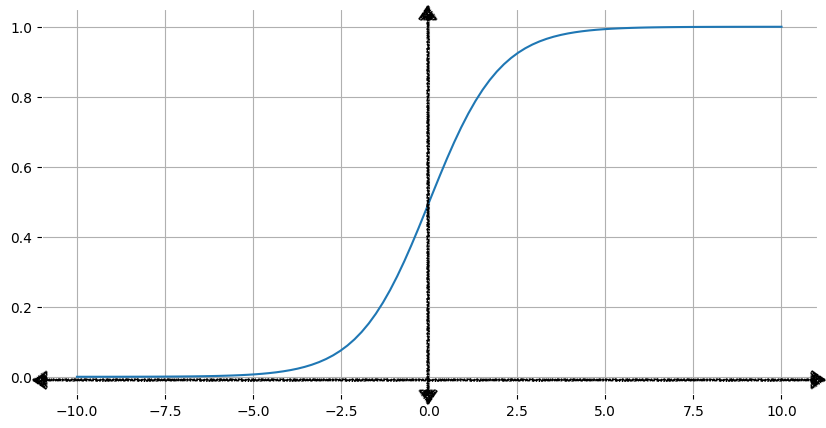
Man mano che l'input x aumenta, l'output della funzione sigmoidea si avvicina a 1, ma non lo raggiunge mai. Analogamente, quando l'input diminuisce, l'output della funzione sigmoidea si avvicina a 0, ma non lo raggiunge mai.

Fai clic qui per un approfondimento sulla matematica dietro la funzione sigmoidea

La tabella seguente mostra i valori di output della funzione sigmoidale per i valori di input nell'intervallo da -7 a 7. Nota la velocità con cui si avvicina la funzione sigmoidea 0 per diminuire i valori di input negativi e la velocità di avvicinamento della funzione sigmoidea 1 per aumentare i valori di input positivi.

Tuttavia, indipendentemente da quanto sia grande o piccolo il valore inserito, l'output sarà sempre maggiore di 0 e minore di 1.

Input	Output sigmoidea
-7	0,001
-6	0,002
-5	0,007
-4	0,018
-3	0,047
-2	0,119
-1	0,269
0	0,50
1	0,731
2	0,881
3	0,952
4	0,982
5	0,993
6	0,997
7	0,999

Trasformazione dell'output lineare mediante la funzione sigmoidea

La seguente equazione rappresenta il componente lineare di un modello di regressione logistica:

\[z = b + w_1x_1 + w_2x_2 + \ldots + w_Nx_N\]

dove:

• z è l'output dell'equazione lineare, chiamata anche probabilità di log:
• b è il bias.
• I valori w sono i pesi appresi dal modello.
• I valori x sono i valori delle caratteristiche per un determinato esempio.

Per ottenere la previsione della regressione logistica, il valore z viene poi passato alla funzione sigmoide, che restituisce un valore (una probabilità) compreso tra 0 e 1:

\[y' = \frac{1}{1 + e^{-z}}\]

dove:

• y' è l'output del modello di regressione logistica.
• z è l'output lineare (come calcolato nell'equazione precedente).

Fai clic qui per scoprire di più sulle probabilità logaritmiche

Nell'equazione $z = b + w_1x_1 + w_2x_2 + \ldots + w_Nx_N$, z viene denominata log-odds perché, se inizi con funzione sigmoidea seguente (dove $y$ è l'output di una funzione di regressione lineare, che rappresenta una probabilità):

$$y = \frac{1}{1 + e^{-z}}$$

e poi risolvi per z:

$$ z = \log\left(\frac{y}{1-y}\right) $$

Quindi z è definito come il logaritmo del rapporto delle probabilità dei due possibili risultati: y e 1 – y.

La Figura 2 illustra come l'output lineare viene trasformato in regressione logistica utilizzando questi calcoli.

Figura 2. A sinistra: grafico della funzione lineare z = 2x + 5 con tre punti evidenziati. A destra: curva sigmoide con gli stessi tre punti evidenziato dopo essere stata trasformata dalla funzione sigmoide.

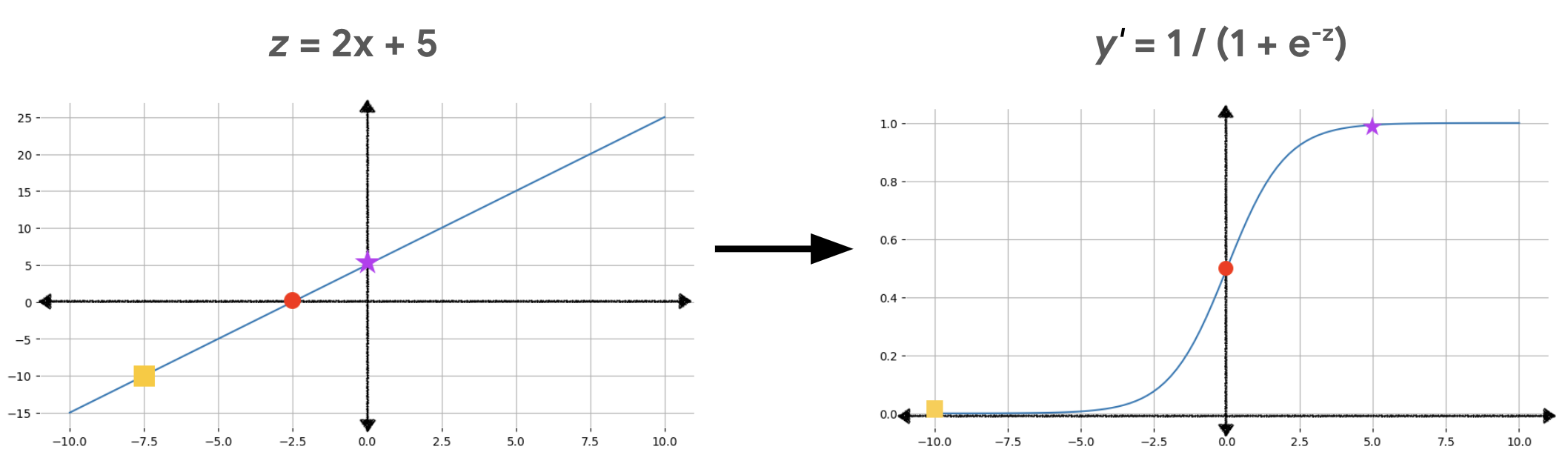
Nella Figura 2, un'equazione lineare diventa l'input della funzione sigmoidea, che piega la linea retta a forma di "S". Nota che l'equazione lineare può produrre valori molto grandi o molto piccoli di z, ma l'output della funzione sigmoidea y, è sempre compresa tra 0 e 1 esclusi. Ad esempio, il quadrato giallo nel grafico a sinistra ha un valore z pari a -10, ma la funzione sigmoidale nel grafico a destra mappa questo valore a -10 in un valore y' pari a 0,00004.

Esercizio: verifica di aver compreso

Un modello di regressione logistica con tre elementi presenta i seguenti bias e pesi:

\[\begin{align} b &= 1 \\ w_1 &= 2 \\ w_2 &= -1 \\ w_3 &= 5 \end{align} \]

Dati i seguenti valori di input:

\[\begin{align} x_1 &= 0 \\ x_2 &= 10 \\ x_3 &= 2 \end{align} \]

Rispondi alle due domande che seguono.

1. Qual è il valore di z per questi valori di input?

-1

0

0,731

1

Esatto! L'equazione lineare definita dalle ponderazioni e dal bias è z = 1 + 2x₁ – x₂ + 5 x₃. Collegare il di input dell'equazione produce z = 1 + (2)(0) - (10) + (5)(2) = 1

2. Qual è la previsione della regressione logistica per questi valori di input?

0,268

0,5

0,731

Come calcolato nel punto 1 sopra, le probabilità logaritmiche per i valori di input sono pari a 1. Collegando il valore di z alla funzione sigmoidea:

\(y = \frac{1}{1 + e^{-z}} = \frac{1}{1 + e^{-1}} = \frac{1}{1 + 0.367} = \frac{1}{1.367} = 0.731\)

1

Ricorda che l'output della funzione sigmoidea sarà sempre maggiore di 0 e minore di 1.

Termini chiave:

• Classificazione binaria
• Registra quote
• Regressione logistica
• Funzione sigmoidea