Логистическая регрессия: вычисление вероятности с помощью сигмовидной функции

Многие задачи требуют на выходе оценки вероятности. Логистическая регрессия — чрезвычайно эффективный механизм расчета вероятностей. Практически говоря, вы можете использовать возвращаемую вероятность одним из следующих двух способов:

• Применяется «как есть». Например, если модель прогнозирования спама принимает электронное письмо в качестве входных данных и выводит значение 0.932 , это подразумевает вероятность 93.2% , что электронное письмо является спамом.

• Преобразуется в двоичную категорию , например True или False , Spam или Not Spam .

В этом модуле основное внимание уделяется использованию выходных данных модели логистической регрессии «как есть». В модуле «Классификация» вы узнаете, как преобразовать эти выходные данные в двоичную категорию.

Сигмовидная функция

Вам может быть интересно, как модель логистической регрессии может гарантировать, что ее выходные данные представляют собой вероятность, всегда выдавая значение от 0 до 1. На самом деле существует семейство функций, называемых логистическими функциями, выходные данные которых имеют те же характеристики. Стандартная логистическая функция, также известная как сигмовидная функция ( сигмовидная означает «s-образная»), имеет формулу:

\[f(x) = \frac{1}{1 + e^{-x}}\]

На рис. 1 показан соответствующий график сигмовидной функции.

Рисунок 1. График сигмовидной функции. Кривая приближается к 0, когда значения x уменьшаются до отрицательной бесконечности, и к 1, когда значения x увеличиваются до бесконечности.

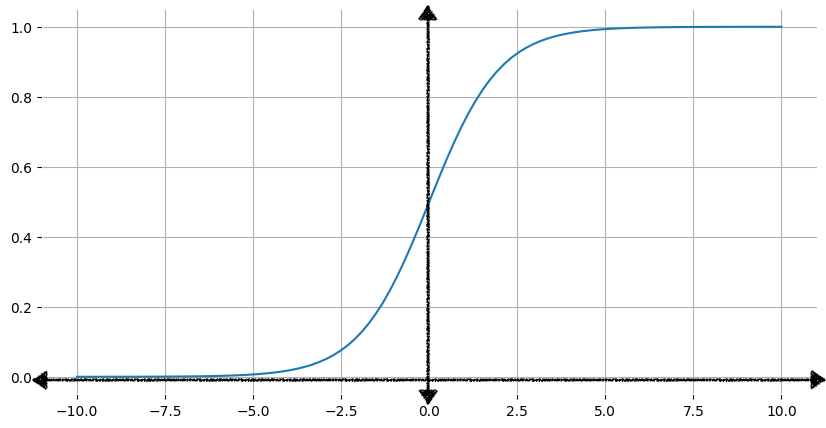
По мере увеличения входного значения x выходной сигнал сигмовидной функции приближается, но никогда не достигает 1 . Точно так же, когда входные данные уменьшаются, выходные данные сигмовидной функции приближаются, но никогда не достигают 0 .

Нажмите здесь, чтобы более глубоко погрузиться в математические расчеты сигмовидной функции.

В таблице ниже показаны выходные значения сигмовидной функции для входных значений в диапазоне от –7 до 7. Обратите внимание, как быстро сигмоида приближается к 0 для уменьшения отрицательных входных значений и как быстро сигмоида приближается к 1 для увеличения положительных входных значений.

Однако независимо от того, насколько велико или мало входное значение, выходное значение всегда будет больше 0 и меньше 1.

Вход	Сигмовидный выход
-7	0,001
-6	0,002
-5	0,007
-4	0,018
-3	0,047
-2	0,119
-1	0,269
0	0,50
1	0,731
2	0,881
3	0,952
4	0,982
5	0,993
6	0,997
7	0,999

Преобразование линейного выхода с помощью сигмовидной функции

Следующее уравнение представляет линейный компонент модели логистической регрессии:

\[z = b + w_1x_1 + w_2x_2 + \ldots + w_Nx_N\]

где:

• z — результат линейного уравнения, также называемый логарифмом шансов .
• б – смещение.
• Значения w представляют собой изученные веса модели.
• Значения x — это значения признаков для конкретного примера.

Чтобы получить прогноз логистической регрессии, значение z затем передается сигмовидной функции, что дает значение (вероятность) от 0 до 1:

\[y' = \frac{1}{1 + e^{-z}}\]

где:

• y' — результат модели логистической регрессии.
• z — линейный выход (рассчитанный в предыдущем уравнении).

Нажмите здесь, чтобы узнать больше о лог-шансах

В уравнении $z = b + w_1x_1 + w_2x_2 + \ldots + w_Nx_N$ z называется логарифмом шансов , потому что если вы начнете со следующей сигмовидной функции (где $y$ — результат модели логистической регрессии, представляющий вероятность):

$$y = \frac{1}{1 + e^{-z}}$$

А затем решите для z :

$$ z = \log\left(\frac{y}{1-y}\right) $$

Тогда z определяется как логарифм отношения вероятностей двух возможных исходов: y и 1 – y .

На рисунке 2 показано, как линейный результат преобразуется в результат логистической регрессии с помощью этих вычислений.

Рисунок 2. Слева: график линейной функции z = 2x + 5, выделены три точки. Справа: сигмовидная кривая с теми же тремя точками, выделенными после преобразования сигмовидной функцией.

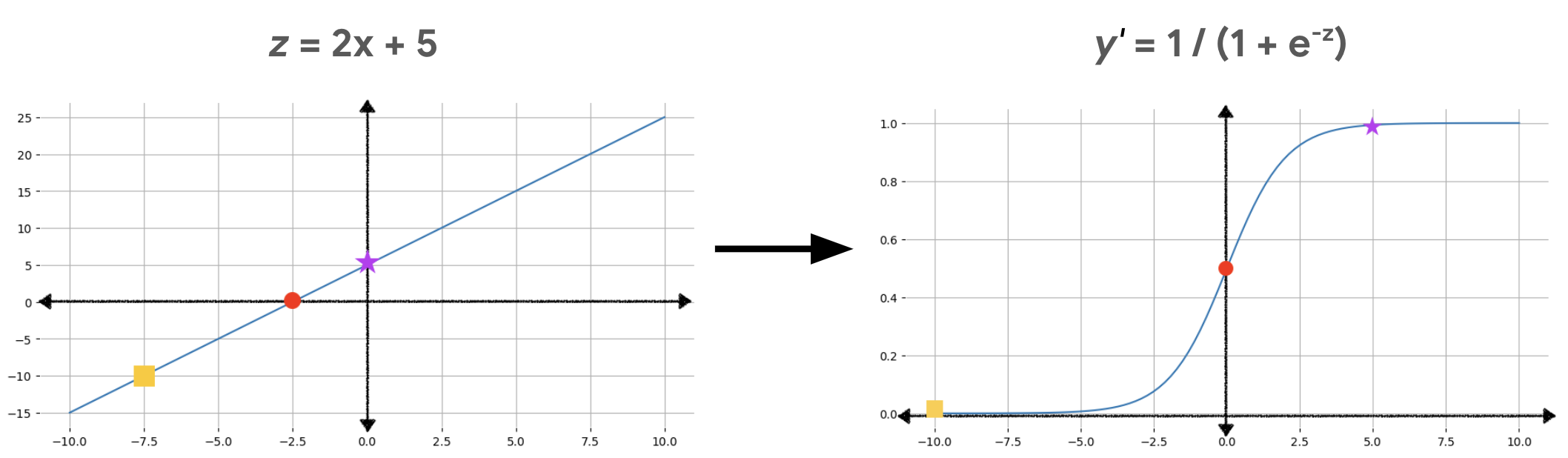
На рисунке 2 линейное уравнение становится входными данными для сигмоидальной функции, которая изгибает прямую линию в S-образную форму. Обратите внимание, что линейное уравнение может выводить очень большие или очень маленькие значения z, но выходные данные сигмоидальной функции y' всегда находятся в диапазоне от 0 до 1, исключая. Например, оранжевый прямоугольник на левом графике имеет значение az -10, но сигмовидная функция на правом графике отображает это значение -10 в значение y', равное 0,00004.

Упражнение: Проверьте свое понимание.

Модель логистической регрессии с тремя функциями имеет следующие смещения и веса:

\[\begin{align} b &= 1 \\ w_1 &= 2 \\ w_2 &= -1 \\ w_3 &= 5 \end{align} \]

Учитывая следующие входные значения:

\[\begin{align} x_1 &= 0 \\ x_2 &= 10 \\ x_3 &= 2 \end{align} \]

Ответьте на следующие два вопроса.

1. Каково значение z для этих входных значений?

–1

0

0,731

1

Правильный! Линейное уравнение, определяемое весами и смещением, имеет вид z = 1 + 2x ₁ – x ₂ + 5 x ₃ . Подстановка входных значений в уравнение дает z = 1 + (2)(0) – (10) + (5)(2) = 1.

2. Каков прогноз логистической регрессии для этих входных значений?

0,268

0,5

0,731

Как рассчитано в пункте 1 выше, логарифмические шансы для входных значений равны 1. Подключаем это значение для z к сигмовидной функции:

\(y = \frac{1}{1 + e^{-z}} = \frac{1}{1 + e^{-1}} = \frac{1}{1 + 0.367} = \frac{1}{1.367} = 0.731\)

1

Помните, что выходные данные сигмовидной функции всегда будут больше 0 и меньше 1.

Ключевые термины:

• Бинарная классификация
• Записать шансы
• Логистическая регрессия
• Сигмовидная функция