Logistische Regression: Berechnung einer Wahrscheinlichkeit mit der Sigmoidfunktion

Für viele Probleme ist eine Wahrscheinlichkeitsschätzung als Ausgabe erforderlich. Die logistische Regression ist ein äußerst effizienter Mechanismus zur Berechnung von Wahrscheinlichkeiten. In der Praxis können Sie die zurückgegebene Wahrscheinlichkeit auf zwei Arten verwenden:

• „Wie sie ist“ angewendet. Wenn ein Modell zur Spamvorhersage beispielsweise eine E‑Mail als Eingabe verwendet und den Wert 0.932 ausgibt, bedeutet das, dass die Wahrscheinlichkeit, dass die E‑Mail Spam ist, bei 93.2% liegt.

• In eine binäre Kategorie wie True oder False, Spam oder Not Spam umgewandelt.

In diesem Modul geht es darum, die Ausgabe von logistischen Regressionsmodellen unverändert zu verwenden. Im Klassifizierungsmodul erfahren Sie, wie Sie diese Ausgabe in eine binäre Kategorie umwandeln.

Sigmoidfunktion

Sie fragen sich vielleicht, wie ein logistisches Regressionsmodell sicherstellen kann, dass seine Ausgabe eine Wahrscheinlichkeit darstellt und immer einen Wert zwischen 0 und 1 ausgibt. Es gibt eine Familie von Funktionen, die logistische Funktionen genannt werden und deren Ausgabe dieselben Eigenschaften hat. Die Standard-Logistikfunktion, auch Sigmoidfunktion genannt (sigmoid bedeutet „S-förmig“), hat die folgende Formel:

\[f(x) = \frac{1}{1 + e^{-x}}\]

Dabei gilt:

• f(x) ist die Ausgabe der Sigmoid-Funktion.
• e ist die Eulersche Zahl: eine mathematische Konstante ≈ 2,71828.
• x ist die Eingabe für die Sigmoidfunktion.

Abbildung 1 zeigt den entsprechenden Graphen der Sigmoidfunktion.

Abbildung 1. Graph der Sigmoidfunktion. Die Kurve nähert sich 0 an, wenn die x-Werte gegen minus unendlich gehen, und 1, wenn die x-Werte gegen unendlich gehen.

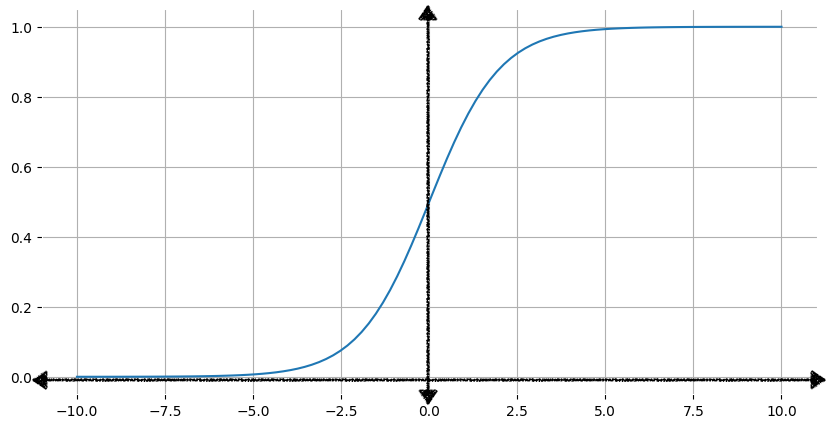
Wenn der Eingabewert x steigt, nähert sich die Ausgabe der Sigmoid-Funktion dem Wert 1 an, erreicht ihn aber nie. Wenn die Eingabe abnimmt, nähert sich die Ausgabe der Sigmoid-Funktion dem Wert 0 an, erreicht ihn aber nie.

Weitere Informationen zur Mathematik hinter der Sigmoidfunktion

In der folgenden Tabelle sind die Ausgabewerte der Sigmoid-Funktion für Eingabewerte im Bereich von -7 bis 7 aufgeführt. Beachten Sie, wie schnell sich die Sigmoidfunktion für abnehmende negative Eingabewerte an 0 und für zunehmende positive Eingabewerte an 1 annähert.

Unabhängig davon, wie groß oder klein der Eingabewert ist, liegt der Ausgabewert immer zwischen 0 und 1.

Eingabe	Sigmoid-Ausgabe
-7	0,001
-6	0,002
-5	0,007
-4	0,018
-3	0,047
-2	0,119
-1	0,269
0	0,50
1	0,731
2	0,881
3	0,952
4	0,982
5	0,993
6	0,997
7	0,999

Lineare Ausgabe mit der Sigmoid-Funktion transformieren

Die folgende Gleichung stellt die lineare Komponente eines logistischen Regressionsmodells dar:

\[z = b + w_1x_1 + w_2x_2 + \ldots + w_Nx_N\]

Dabei gilt:

• z ist die Ausgabe der linearen Gleichung, auch Log-Odds genannt.
• b ist der Bias.
• Die w-Werte sind die gelernten Gewichte des Modells.
• Die x-Werte sind die Feature-Werte für ein bestimmtes Beispiel.

Um die Vorhersage für die logistische Regression zu erhalten, wird der z-Wert dann an die Sigmoid-Funktion übergeben, was einen Wert (eine Wahrscheinlichkeit) zwischen 0 und 1 ergibt:

\[y' = \frac{1}{1 + e^{-z}}\]

Dabei gilt:

• y' ist die Ausgabe des logistischen Regressionsmodells.
• e ist die Eulersche Zahl: eine mathematische Konstante ≈ 2,71828.
• z ist die lineare Ausgabe (wie in der vorherigen Gleichung berechnet).

Weitere Informationen zu Log-Odds

In der Gleichung $z = b + w_1x_1 + w_2x_2 + \ldots + w_Nx_N$ wird z als Logit bezeichnet, da sie aus der folgenden Sigmoid-Funktion abgeleitet wird (wobei $y$ die Ausgabe eines logistischen Regressionsmodells ist, das eine Wahrscheinlichkeit darstellt):

$$y = \frac{1}{1 + e^{-z}}$$

Lösen Sie dann nach z auf:

$$ z = \log\left(\frac{y}{1-y}\right) $$

z ist dann als der Logarithmus des Verhältnisses der Wahrscheinlichkeiten der beiden möglichen Ergebnisse y und 1 – y definiert.

Abbildung 2 veranschaulicht, wie die lineare Ausgabe mithilfe dieser Berechnungen in die Ausgabe der logistischen Regression transformiert wird.

Abbildung 2. Links: Diagramm der linearen Funktion z = 2x + 5 mit drei hervorgehobenen Punkten. Rechts: Sigmoid-Kurve mit denselben drei Punkten, die nach der Transformation durch die Sigmoid-Funktion hervorgehoben werden.

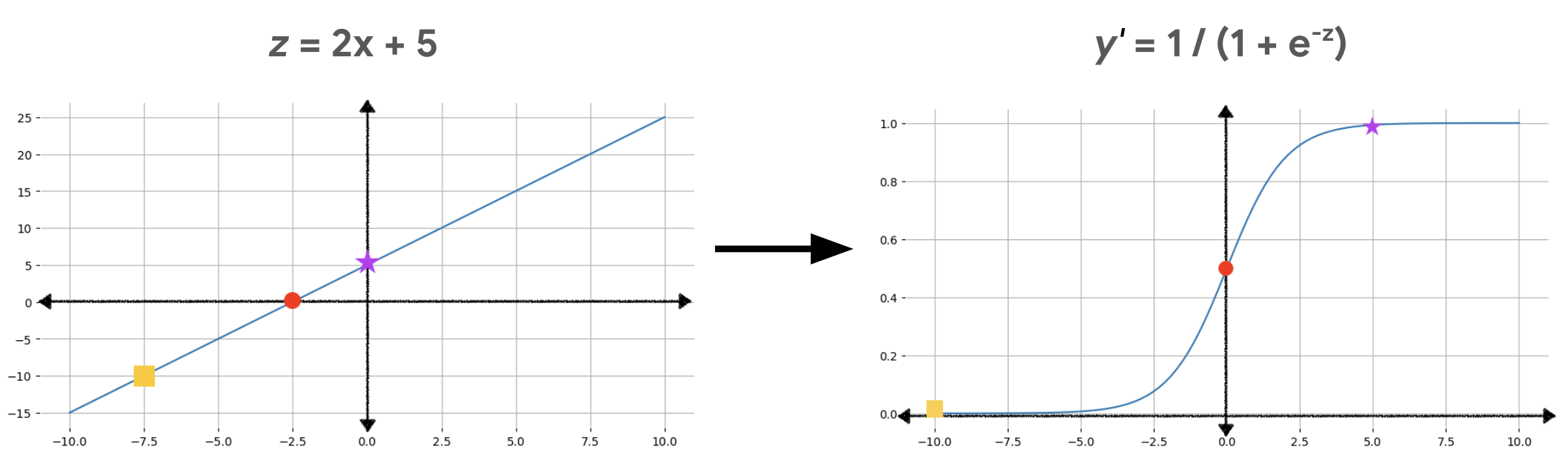
In Abbildung 2 wird eine lineare Gleichung in die Sigmoid-Funktion eingegeben, wodurch die gerade Linie in eine S-Form gebogen wird. Die lineare Gleichung kann sehr große oder sehr kleine Werte für z ausgeben, die Ausgabe der Sigmoid-Funktion (y') liegt jedoch immer zwischen 0 und 1 (exklusiv). Das gelbe Quadrat im linken Diagramm hat beispielsweise einen z-Wert von -10.Die Sigmoid-Funktion im rechten Diagramm ordnet diesem Wert jedoch einen y'-Wert von 0,00004 zu.

Übung: Wissen testen

Ein logistisches Regressionsmodell mit drei Features hat den folgenden Bias und die folgenden Gewichte:

\[\begin{align} b &= 1 \\ w_1 &= 2 \\ w_2 &= -1 \\ w_3 &= 5 \end{align} \]

Angenommen, die folgenden Eingabewerte sind vorhanden:

\[\begin{align} x_1 &= 0 \\ x_2 &= 10 \\ x_3 &= 2 \end{align} \]

Beantworten Sie die folgenden Fragen.

1. Welchen Wert hat z für diese Eingabewerte?

–1

0

0,731

1

Richtig! Die durch die Gewichte und den Bias definierte lineare Gleichung lautet: z = 1 + 2x₁ – x₂ + 5x₃. Wenn Sie die Eingabewerte in die Gleichung einsetzen, erhalten Sie z = 1 + (2)(0) – (10) + (5)(2) = 1.

2. Wie lautet die Vorhersage der logistischen Regression für diese Eingabewerte?

0,268

0,5

0,731

Wie in Schritt 1 berechnet, beträgt der Log-Odds-Wert für die Eingabewerte 1. Wenn wir diesen Wert für z in die Sigmoid-Funktion einsetzen, erhalten wir:

\(y = \frac{1}{1 + e^{-z}} = \frac{1}{1 + e^{-1}} = \frac{1}{1 + 0.367} = \frac{1}{1.367} = 0.731\)

1

Die Ausgabe der Sigmoid-Funktion ist immer größer als 0 und kleiner als 1.

Wichtige Begriffe:

• Binärklassifizierung
• Log-Odds
• Logistische Regression
• Sigmoidfunktion