Regresi logistik: Menghitung probabilitas dengan fungsi sigmoid

Banyak masalah memerlukan estimasi probabilitas sebagai output. Regresi logistik adalah mekanisme yang sangat efisien untuk menghitung probabilitas. Secara praktis, Anda dapat menggunakan probabilitas yang ditampilkan dengan salah satu dari dua cara berikut:

• Diterapkan "apa adanya". Misalnya, jika model prediksi spam mengambil email sebagai input dan menghasilkan nilai 0.932, ini menyiratkan probabilitas 93.2% bahwa email tersebut adalah spam.

• Dikonversi menjadi kategori biner seperti True atau False, Spam atau Not Spam.

Modul ini berfokus pada penggunaan output model regresi logistik apa adanya. Dalam modul Klasifikasi, Anda akan mempelajari cara mengonversi output ini menjadi kategori biner.

Fungsi sigmoid

Anda mungkin bertanya-tanya bagaimana model regresi logistik dapat memastikan outputnya merepresentasikan probabilitas, yang selalu menghasilkan nilai antara 0 dan 1. Ternyata, ada sekumpulan fungsi yang disebut fungsi logistik yang keluarannya memiliki karakteristik yang sama. Fungsi logistik standar, juga dikenal sebagai fungsi sigmoid (sigmoid berarti "berbentuk s"), memiliki rumus:

\[f(x) = \frac{1}{1 + e^{-x}}\]

dalam hal ini:

• f(x) adalah output dari fungsi sigmoid.
• e adalah bilangan Euler: konstanta matematika ≈ 2,71828.
• x adalah input ke fungsi sigmoid.

Gambar 1 menunjukkan grafik fungsi sigmoid yang sesuai.

Gambar 1. Grafik fungsi sigmoid. Kurva mendekati 0 saat nilai x menurun hingga negatif tak terhingga, dan 1 saat nilai x meningkat menuju tak terhingga.

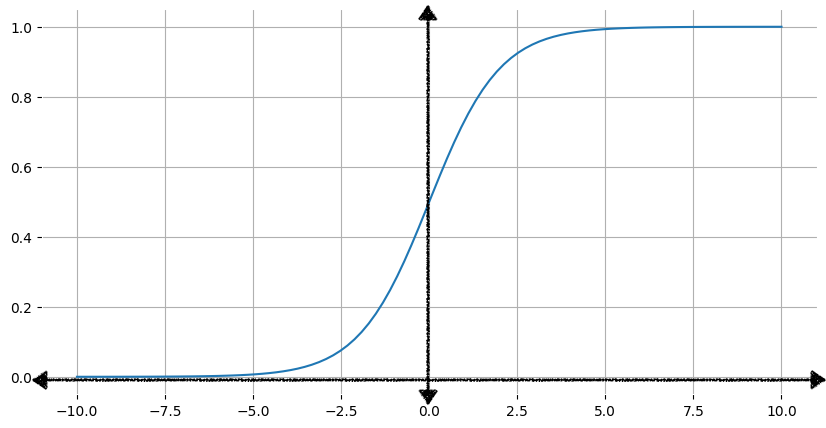
Saat input, x, meningkat, output fungsi sigmoid mendekati tetapi tidak pernah mencapai 1. Demikian pula, saat input berkurang, output fungsi sigmoid mendekati 0, tetapi tidak pernah mencapainya.

Klik di sini untuk mempelajari lebih dalam matematika di balik fungsi sigmoid

Tabel di bawah menunjukkan nilai output fungsi sigmoid untuk nilai input dalam rentang –7 hingga 7. Perhatikan seberapa cepat sigmoid mendekati 0 untuk nilai input negatif yang menurun, dan seberapa cepat sigmoid mendekati 1 untuk nilai input positif yang meningkat.

Namun, tidak peduli seberapa besar atau kecil nilai input, output akan selalu lebih besar dari 0 dan kurang dari 1.

Input	Output sigmoid
-7	0,001
-6	0,002
-5	0,007
-4	0,018
-3	0,047
-2	0,119
-1	0,269
0	0,50
1	0,731
2	0,881
3	0,952
4	0,982
5	0,993
6	0,997
7	0,999

Mengubah output linier menggunakan fungsi sigmoid

Persamaan berikut merepresentasikan komponen linear model regresi logistik:

\[z = b + w_1x_1 + w_2x_2 + \ldots + w_Nx_N\]

dalam hal ini:

• z adalah output persamaan linear, yang juga disebut log odds.
• b adalah bias.
• Nilai w adalah bobot model yang dipelajari.
• Nilai x adalah nilai fitur untuk contoh tertentu.

Untuk mendapatkan prediksi regresi logistik, nilai z kemudian diteruskan ke fungsi sigmoid, yang menghasilkan nilai (probabilitas) antara 0 dan 1:

\[y' = \frac{1}{1 + e^{-z}}\]

dalam hal ini:

• y' adalah output model regresi logistik.
• e adalah bilangan Euler: konstanta matematika ≈ 2,71828.
• z adalah output linear (seperti yang dihitung dalam persamaan sebelumnya).

Klik di sini untuk mempelajari lebih lanjut log-odds

Dalam persamaan $z = b + w_1x_1 + w_2x_2 + \ldots + w_Nx_N$, z disebut sebagai log-odds karena jika Anda memulai dengan fungsi sigmoid berikut (dengan $y$ adalah output model regresi logistik, yang merepresentasikan probabilitas):

$$y = \frac{1}{1 + e^{-z}}$$

Kemudian, selesaikan z:

$$ z = \log\left(\frac{y}{1-y}\right) $$

Kemudian, z ditentukan sebagai log rasio probabilitas dari dua kemungkinan hasil: y dan 1 – y.

Gambar 2 menggambarkan cara output linear diubah menjadi output regresi logistik menggunakan perhitungan ini.

Gambar 2. Kiri: grafik fungsi linear z = 2x + 5, dengan tiga titik ditandai. Kanan: Kurva sigmoid dengan tiga titik yang sama ditandai setelah diubah oleh fungsi sigmoid.

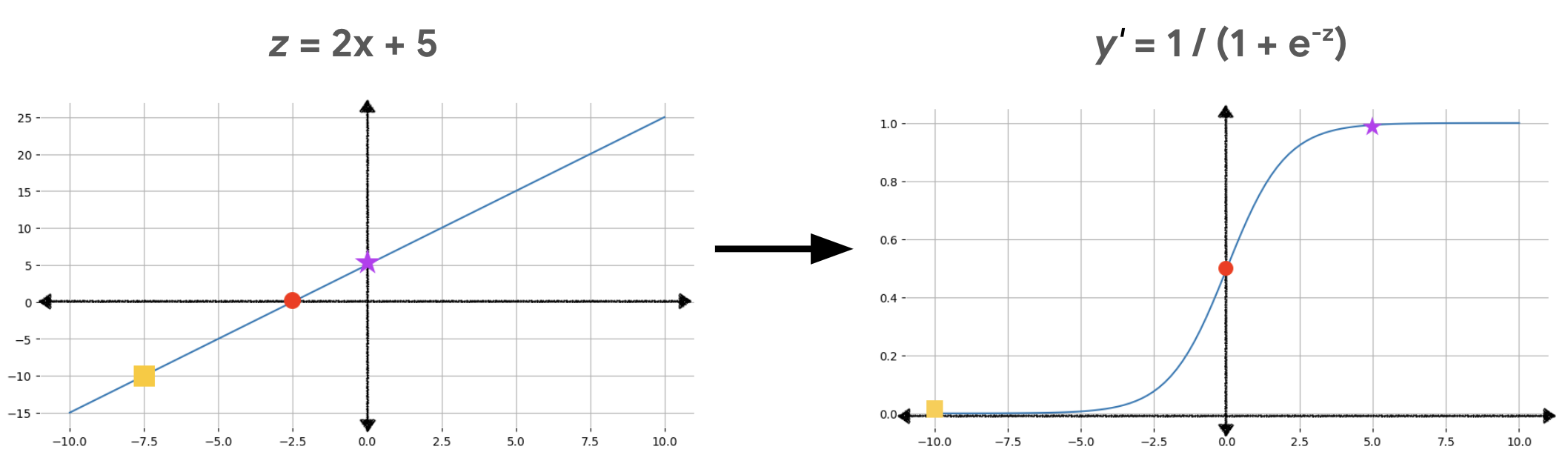
Pada Gambar 2, persamaan linear menjadi input ke fungsi sigmoid, yang membelokkan garis lurus menjadi bentuk s. Perhatikan bahwa persamaan linear dapat menghasilkan nilai z yang sangat besar atau sangat kecil, tetapi output fungsi sigmoid, y', selalu antara 0 dan 1, secara eksklusif. Misalnya, persegi kuning pada grafik kiri memiliki nilai z –10, tetapi fungsi sigmoid dalam grafik kanan memetakan –10 tersebut ke nilai y' 0,00004.

Latihan: Periksa pemahaman Anda

Model regresi logistik dengan tiga fitur memiliki bias dan bobot berikut:

\[\begin{align} b &= 1 \\ w_1 &= 2 \\ w_2 &= -1 \\ w_3 &= 5 \end{align} \]

Dengan nilai input berikut:

\[\begin{align} x_1 &= 0 \\ x_2 &= 10 \\ x_3 &= 2 \end{align} \]

Jawablah dua pertanyaan berikut.

1. Berapa nilai z untuk nilai input ini?

–1

0

0,731

1

Benar. Persamaan linear yang ditentukan oleh bobot dan bias adalah z = 1 + 2x₁ – x₂ + 5 x₃. Dengan memasukkan nilai input ke dalam persamaan, akan menghasilkan z = 1 + (2)(0) - (10) + (5)(2) = 1

2. Berapa prediksi regresi logistik untuk nilai input ini?

0,268

0,5

0,731

Seperti yang dihitung pada #1 di atas, log-peluang untuk nilai input adalah 1. Menyisipkan nilai z tersebut ke dalam fungsi sigmoid:

\(y = \frac{1}{1 + e^{-z}} = \frac{1}{1 + e^{-1}} = \frac{1}{1 + 0.367} = \frac{1}{1.367} = 0.731\)

1

Ingat, output fungsi sigmoid akan selalu lebih besar dari 0 dan kurang dari 1.

Istilah utama:

• Klasifikasi biner
• Peluang log
• Regresi logistik
• Fungsi sigmoid