多くの問題では、確率推定値が出力として必要になります。ロジスティック回帰は、確率を計算するための非常に効率的なメカニズムです。実際には、返された確率は次の 2 つの方法で使用できます。
「そのまま」適用されます。たとえば、スパム予測モデルがメールを入力として受け取り、
0.932の値を出力する場合、そのメールがスパムである確率は93.2%です。True、False、Spam、Not Spamなどのバイナリ カテゴリに変換されます。
このモジュールでは、ロジスティック回帰モデルの出力をそのまま使用することに焦点を当てます。分類モジュールでは、この出力をバイナリ カテゴリに変換する方法について学習します。
シグモイド関数
ロジスティック回帰モデルが確率を表す出力を保証し、常に 0 ~ 1 の値を出力できるのはなぜでしょうか。偶然にも、出力に同じ特性を持つロジスティック関数という関数群があります。標準ロジスティック関数(シグモイド関数とも呼ばれます。sigmoidは「S 字型」を意味します)の式は次のとおりです。
\[f(x) = \frac{1}{1 + e^{-x}}\]
ここで
- f(x) はシグモイド関数の出力です。
- e はオイラー数です。数学定数 ≈ 2.71828。
- x はシグモイド関数への入力です。
図 1 は、シグモイド関数の対応するグラフを示しています。
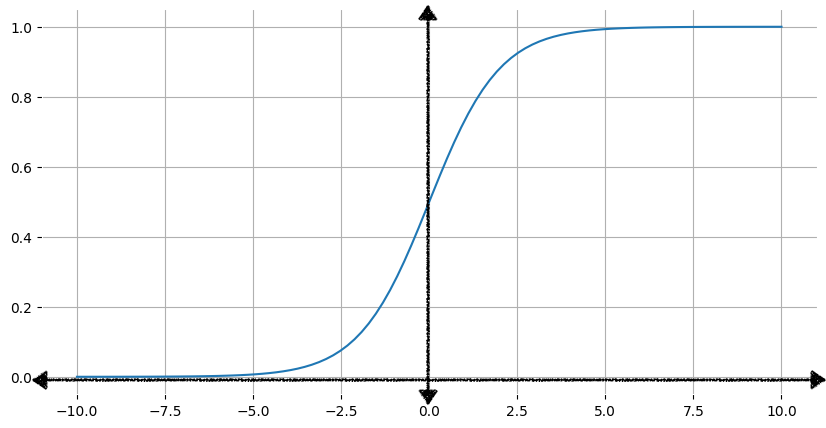
入力 x が増加すると、シグモイド関数の出力は 1 に近づきますが、1 に達することはありません。同様に、入力が減少すると、シグモイド関数の出力は 0 に近づきますが、0 に達することはありません。
シグモイド関数の背後にある数学の詳細については、こちらをクリックしてください
次の表に、入力値が -7 ~ 7 の範囲の場合のシグモイド関数の出力値を示します。負の入力値が減少するとシグモイドが 0 に近づく速度と、正の入力値が増加するとシグモイドが 1 に近づく速度に注目してください。
ただし、入力値の大小にかかわらず、出力は常に 0 より大きく 1 より小さくなります。
| 入力 | シグモイド出力 |
|---|---|
| -7 | 0.001 |
| -6 | 0.002 |
| -5 | 0.007 |
| -4 | 0.018 |
| -3 | 0.047 |
| -2 | 0.119 |
| -1 | 0.269 |
| 0 | 0.50 |
| 1 | 0.731 |
| 2 | 0.881 |
| 3 | 0.952 |
| 4 | 0.982 |
| 5 | 0.993 |
| 6 | 0.997 |
| 7 | 0.999 |
シグモイド関数を使用して線形出力を変換する
次の式は、ロジスティック回帰モデルの線形コンポーネントを表しています。
\[z = b + w_1x_1 + w_2x_2 + \ldots + w_Nx_N\]
ここで
- z は線形方程式の出力であり、対数オッズとも呼ばれます。
- b はバイアスです。
- w 値は、モデルの学習済み重みです。
- x 値は、特定の例の特徴値です。
ロジスティック回帰予測を取得するには、z 値をシグモイド関数に渡して、0 ~ 1 の範囲の値(確率)を取得します。
\[y' = \frac{1}{1 + e^{-z}}\]
ここで
- y' は、ロジスティック回帰モデルの出力です。
- e はオイラー数です。数学定数 ≈ 2.71828。
- z は線形出力です(前述の式で計算)。
ログオッズの詳細については、こちらをクリックしてください
方程式 $z = b + w_1x_1 + w_2x_2 + \ldots + w_Nx_N$ では、次のシグモイド関数($y$ はロジスティック回帰モデルの出力で、確率を表します)から始めると、z は対数オッズと呼ばれます。
$$y = \frac{1}{1 + e^{-z}}$$
次に、z について解きます。
$$ z = \ln\left(\frac{y}{1-y}\right) $$
z は、2 つの結果(y と 1 – y)の確率の比率の自然対数として定義されます。
図 2 は、これらの計算を使用して線形出力をロジスティック回帰出力に変換する方法を示しています。
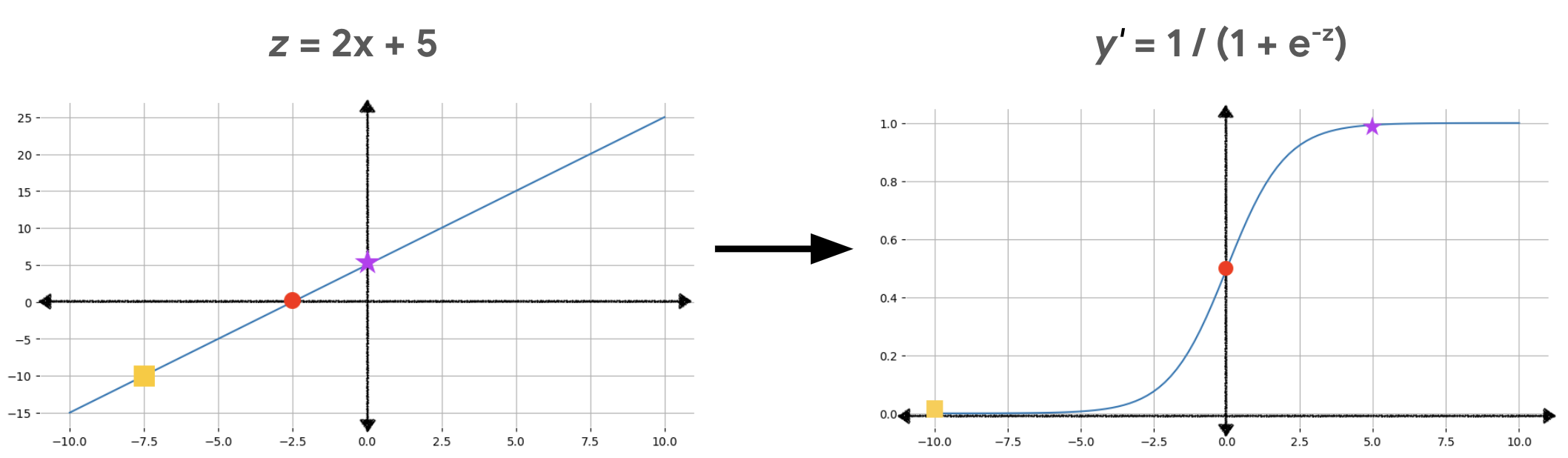
図 2 では、線形方程式がシグモイド関数の入力になり、直線が S 字型に曲がっています。線形方程式は z の非常に大きな値または非常に小さな値を出力できますが、シグモイド関数の出力 y' は常に 0 から 1 の範囲になります。たとえば、左側のグラフの黄色の正方形の z 値は -10 ですが、右側のグラフのシグモイド関数は、その -10 を y' 値 0.00004 にマッピングします。
演習: 理解度を確認する
3 つの特徴を持つロジスティック回帰モデルには、次のバイアスと重みがあります。
\[\begin{align} b &= 1 \\ w_1 &= 2 \\ w_2 &= -1 \\ w_3 &= 5 \end{align} \]
次の入力値が指定されているとします。
\[\begin{align} x_1 &= 0 \\ x_2 &= 10 \\ x_3 &= 2 \end{align} \]
次の 2 つの質問に答えてください。
上記の #1 で計算したように、入力値の対数オッズは 1 です。z の値をシグモイド関数に代入します。
\(y = \frac{1}{1 + e^{-z}} = \frac{1}{1 + e^{-1}} = \frac{1}{1 + 0.367} = \frac{1}{1.367} = 0.731\)