অনেক সমস্যার আউটপুট হিসাবে একটি সম্ভাব্যতা অনুমান প্রয়োজন। সম্ভাব্যতা গণনা করার জন্য লজিস্টিক রিগ্রেশন একটি অত্যন্ত দক্ষ প্রক্রিয়া। ব্যবহারিকভাবে বলতে গেলে, আপনি নিম্নলিখিত দুটি উপায়ে ফেরত সম্ভাব্যতা ব্যবহার করতে পারেন:
প্রয়োগ করা হয়েছে "যেমন আছে।" উদাহরণস্বরূপ, যদি একটি স্প্যাম-পূর্বাভাস মডেল ইনপুট হিসাবে একটি ইমেল নেয় এবং
0.932এর মান আউটপুট করে, তাহলে এটি93.2%সম্ভাবনা বোঝায় যে ইমেলটি স্প্যাম।TrueবাFalse,SpamবাNot Spamএর মতো একটি বাইনারি বিভাগে রূপান্তর করা হয়েছে৷
এই মডিউলটি লজিস্টিক রিগ্রেশন মডেল আউটপুট যেমন-ই ব্যবহার করার উপর ফোকাস করে। শ্রেণীবিভাগ মডিউলে , আপনি শিখবেন কিভাবে এই আউটপুটটিকে একটি বাইনারি বিভাগে রূপান্তর করতে হয়।
সিগময়েড ফাংশন
আপনি হয়তো ভাবছেন কিভাবে একটি লজিস্টিক রিগ্রেশন মডেল নিশ্চিত করতে পারে যে তার আউটপুট একটি সম্ভাব্যতার প্রতিনিধিত্ব করে, সর্বদা 0 এবং 1 এর মধ্যে একটি মান আউটপুট করে। যেমনটি ঘটে, লজিস্টিক ফাংশন নামে একটি ফাংশন রয়েছে যার আউটপুটে একই বৈশিষ্ট্য রয়েছে। স্ট্যান্ডার্ড লজিস্টিক ফাংশন, যা সিগময়েড ফাংশন নামেও পরিচিত ( সিগময়েড মানে "এস-আকৃতির"), এর সূত্র রয়েছে:
\[f(x) = \frac{1}{1 + e^{-x}}\]
চিত্র 1 সিগমায়েড ফাংশনের সংশ্লিষ্ট গ্রাফ দেখায়।
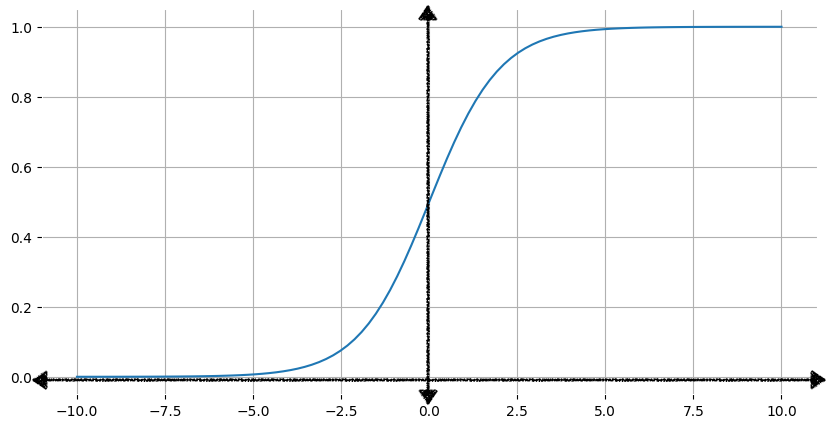
ইনপুট, x , বাড়ার সাথে সাথে সিগমায়েড ফাংশনের আউটপুট কাছে আসে কিন্তু কখনই 1 পৌঁছায় না। একইভাবে, ইনপুট কমার সাথে সাথে সিগমায়েড ফাংশনের আউটপুট কাছে আসে কিন্তু কখনই 0 পৌঁছায় না।
সিগমায়েড ফাংশনের পিছনে গণিতের গভীরে ডুব দেওয়ার জন্য এখানে ক্লিক করুন
নিচের সারণীটি –7 থেকে 7 পরিসরে ইনপুট মানগুলির জন্য সিগময়েড ফাংশনের আউটপুট মানগুলি দেখায়৷ নেতিবাচক ইনপুট মানগুলি হ্রাস করার জন্য সিগময়েড কত দ্রুত 0-এর কাছে পৌঁছায় এবং ইতিবাচক ইনপুট মান বৃদ্ধির জন্য সিগময়েড কত দ্রুত 1-এর কাছে পৌঁছায় তা লক্ষ্য করুন৷
যাইহোক, ইনপুট মান যত বড় বা যতই ছোট হোক না কেন, আউটপুট সর্বদা 0 এর থেকে বেশি এবং 1 এর কম হবে।
| ইনপুট | সিগময়েড আউটপুট |
|---|---|
| -7 | 0.001 |
| -6 | 0.002 |
| -5 | 0.007 |
| -4 | 0.018 |
| -3 | 0.047 |
| -2 | 0.119 |
| -1 | 0.269 |
| 0 | 0.50 |
| 1 | 0.731 |
| 2 | 0.881 |
| 3 | 0.952 |
| 4 | 0.982 |
| 5 | 0.993 |
| 6 | 0.997 |
| 7 | 0.999 |
সিগময়েড ফাংশন ব্যবহার করে রৈখিক আউটপুট রূপান্তর
নিম্নলিখিত সমীকরণটি একটি লজিস্টিক রিগ্রেশন মডেলের রৈখিক উপাদান উপস্থাপন করে:
\[z = b + w_1x_1 + w_2x_2 + \ldots + w_Nx_N\]
কোথায়:
- z হল রৈখিক সমীকরণের আউটপুট, যাকে লগ অডসও বলা হয়।
- b হল পক্ষপাত।
- w মান হল মডেলের শেখা ওজন।
- x মানগুলি একটি নির্দিষ্ট উদাহরণের বৈশিষ্ট্য মান।
লজিস্টিক রিগ্রেশন পূর্বাভাস পেতে, z মানটি সিগমায়েড ফাংশনে প্রেরণ করা হয়, 0 এবং 1 এর মধ্যে একটি মান (সম্ভাব্যতা) প্রদান করে:
\[y' = \frac{1}{1 + e^{-z}}\]
কোথায়:
- y' হল লজিস্টিক রিগ্রেশন মডেলের আউটপুট।
- z হল রৈখিক আউটপুট (পূর্ববর্তী সমীকরণে গণনা করা হয়েছে)।
লগ-অডস সম্পর্কে আরও জানতে এখানে ক্লিক করুন
সমীকরণ $z = b + w_1x_1 + w_2x_2 + \ldots + w_Nx_N$, z কে লগ-অডস হিসাবে উল্লেখ করা হয় কারণ আপনি যদি নিম্নলিখিত সিগমায়েড ফাংশন দিয়ে শুরু করেন (যেখানে $y$ হল একটি লজিস্টিক রিগ্রেশন মডেলের আউটপুট, একটি সম্ভাবনা প্রতিনিধিত্ব করে):
$$y = \frac{1}{1 + e^{-z}}$$
এবং তারপর z এর জন্য সমাধান করুন:
$$ z = \log\left(\frac{y}{1-y}\right) $$
তারপর z কে দুটি সম্ভাব্য ফলাফলের সম্ভাব্যতার অনুপাতের লগ হিসাবে সংজ্ঞায়িত করা হয়: y এবং 1 – y ।
চিত্র 2 এই গণনাগুলি ব্যবহার করে কীভাবে রৈখিক আউটপুট লজিস্টিক রিগ্রেশন আউটপুটে রূপান্তরিত হয় তা ব্যাখ্যা করে।
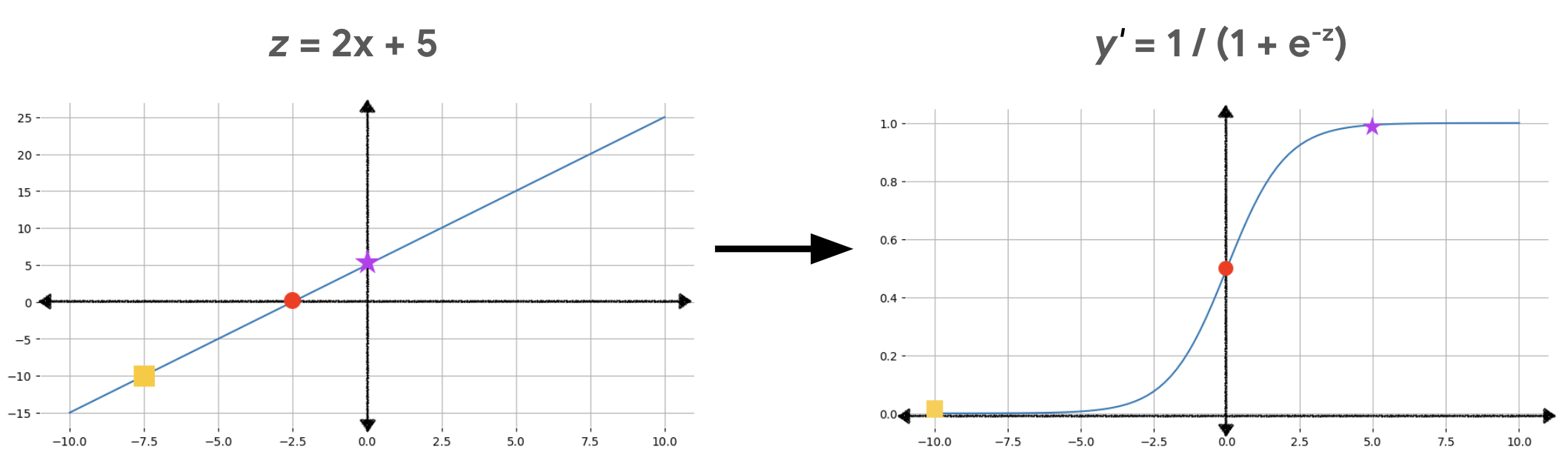
চিত্র 2-এ, একটি রৈখিক সমীকরণ সিগমায়েড ফাংশনে ইনপুট হয়ে যায়, যা সরলরেখাটিকে একটি s-আকৃতিতে বাঁকিয়ে দেয়। লক্ষ্য করুন যে রৈখিক সমীকরণটি z এর খুব বড় বা খুব ছোট মান আউটপুট করতে পারে, কিন্তু সিগমায়েড ফাংশনের আউটপুট, y', সর্বদা 0 এবং 1 এর মধ্যে থাকে, একচেটিয়া। উদাহরণস্বরূপ, বাম গ্রাফের কমলা আয়তক্ষেত্রের az মান -10 আছে, কিন্তু ডান গ্রাফের সিগমায়েড ফাংশনটি -10-কে 0.00004 এর y' মান হিসাবে চিহ্নিত করে।
অনুশীলন: আপনার বোঝার পরীক্ষা করুন
তিনটি বৈশিষ্ট্য সহ একটি লজিস্টিক রিগ্রেশন মডেলের নিম্নলিখিত পক্ষপাত এবং ওজন রয়েছে:
\[\begin{align} b &= 1 \\ w_1 &= 2 \\ w_2 &= -1 \\ w_3 &= 5 \end{align} \]
নিম্নলিখিত ইনপুট মান দেওয়া:
\[\begin{align} x_1 &= 0 \\ x_2 &= 10 \\ x_3 &= 2 \end{align} \]
নিচের দুটি প্রশ্নের উত্তর দাও।
উপরের # 1 এ গণনা করা হয়েছে, ইনপুট মানের জন্য লগ-অডড হল 1। সিগমায়েড ফাংশনে z-এর জন্য সেই মানটিকে প্লাগ করা:
\(y = \frac{1}{1 + e^{-z}} = \frac{1}{1 + e^{-1}} = \frac{1}{1 + 0.367} = \frac{1}{1.367} = 0.731\)