Régression logistique: calculer une probabilité avec la fonction sigmoïde

De nombreux problèmes nécessitent une estimation de probabilité comme résultat. La régression logistique est un mécanisme extrêmement efficace pour calculer des probabilités. Concrètement, vous pouvez utiliser la probabilité renvoyée de l'une des deux manières suivantes :

• Appliqué "tel quel". Par exemple, si un modèle de prédiction du spam prend un e-mail en entrée et génère une valeur de 0.932, cela implique une probabilité de 93.2% que l'e-mail soit du spam.

• Convertie en catégorie binaire, par exemple True ou False, Spam ou Not Spam.

Ce module se concentre sur l'utilisation des résultats du modèle de régression logistique tels quels. Dans le module de classification, vous apprendrez à convertir ces résultats en catégorie binaire.

Fonction sigmoïde

Vous vous demandez peut-être comment un modèle de régression logistique peut s'assurer que sa sortie représente une probabilité, en générant toujours une valeur comprise entre 0 et 1. Il existe une famille de fonctions appelées fonctions logistiques dont la sortie présente ces mêmes caractéristiques. La fonction logistique standard, également appelée fonction sigmoïde (sigmoid signifie "en forme de S"), a la formule suivante :

\[f(x) = \frac{1}{1 + e^{-x}}\]

où :

• f(x) est le résultat de la fonction sigmoïde.
• e est le nombre d'Euler, une constante mathématique ≈ 2,71828.
• x est l'entrée de la fonction sigmoïde.

La figure 1 montre le graphique correspondant de la fonction sigmoïde.

Figure 1. Graphique de la fonction sigmoïde. La courbe tend vers 0 lorsque les valeurs x diminuent vers l'infini négatif, et vers 1 lorsque les valeurs x augmentent vers l'infini.

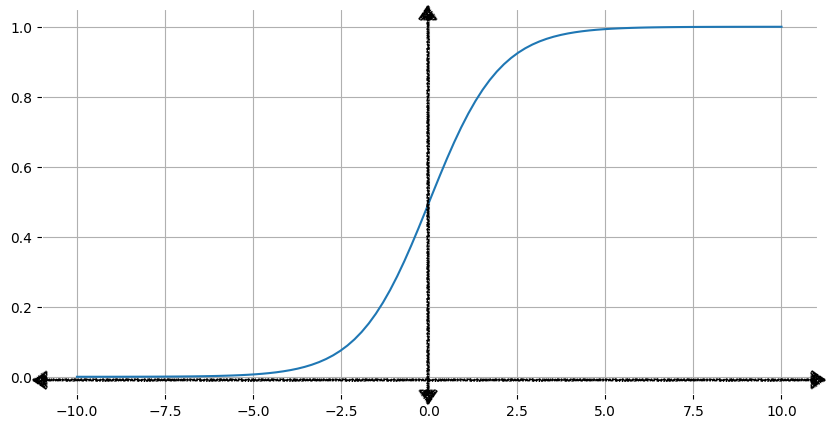
À mesure que l'entrée x augmente, la sortie de la fonction sigmoïde se rapproche de 1, mais ne l'atteint jamais. De même, lorsque l'entrée diminue, la sortie de la fonction sigmoïde s'approche de 0, mais ne l'atteint jamais.

Cliquez ici pour en savoir plus sur les calculs de la fonction sigmoïde.

Le tableau ci-dessous indique les valeurs de sortie de la fonction sigmoïde pour les valeurs d'entrée comprises entre -7 et 7. Notez la rapidité avec laquelle la sigmoïde s'approche de 0 pour les valeurs d'entrée négatives décroissantes et de 1 pour les valeurs d'entrée positives croissantes.

Toutefois, quelle que soit la taille de la valeur d'entrée, la valeur de sortie sera toujours supérieure à 0 et inférieure à 1.

Entrée	Sortie sigmoïde
-7	0,001
-6	0.002
-5	0,007
-4	0,018
-3	0.047
-2	0.119
-1	0,269
0	0.50
1	0.731
2	0.881
3	0.952
4	0.982
5	0.993
6	0.997
7	0.999

Transformer la sortie linéaire à l'aide de la fonction sigmoïde

L'équation suivante représente le composant linéaire d'un modèle de régression logistique :

\[z = b + w_1x_1 + w_2x_2 + \ldots + w_Nx_N\]

où :

• z est le résultat de l'équation linéaire, également appelé log odds.
• b correspond au biais.
• Les valeurs w sont les pondérations apprises par le modèle.
• Les valeurs x sont les valeurs des caractéristiques pour un exemple particulier.

Pour obtenir la prédiction de régression logistique, la valeur z est ensuite transmise à la fonction sigmoïde, ce qui donne une valeur (une probabilité) comprise entre 0 et 1 :

\[y' = \frac{1}{1 + e^{-z}}\]

où :

• y' est le résultat du modèle de régression logistique.
• e est le nombre d'Euler, une constante mathématique ≈ 2,71828.
• z correspond à la sortie linéaire (calculée dans l'équation précédente).

Cliquez ici pour en savoir plus sur les log-odds.

Dans l'équation $z = b + w_1x_1 + w_2x_2 + \ldots + w_Nx_N$, z est appelé log-odds (logarithme de cote). En effet, si vous commencez par la fonction sigmoïde suivante (où $y$ est la sortie d'un modèle de régression logistique, représentant une probabilité) :

$$y = \frac{1}{1 + e^{-z}}$$

Résolvez ensuite l'équation pour z :

$$ z = \log\left(\frac{y}{1-y}\right) $$

z est ensuite défini comme le logarithme du rapport des probabilités des deux résultats possibles : y et 1 – y.

La figure 2 illustre la façon dont la sortie linéaire est transformée en sortie de régression logistique à l'aide de ces calculs.

Figure 2. À gauche : graphique de la fonction linéaire z = 2x + 5, avec trois points mis en évidence. À droite : courbe sigmoïde avec les trois mêmes points mis en évidence après avoir été transformés par la fonction sigmoïde.

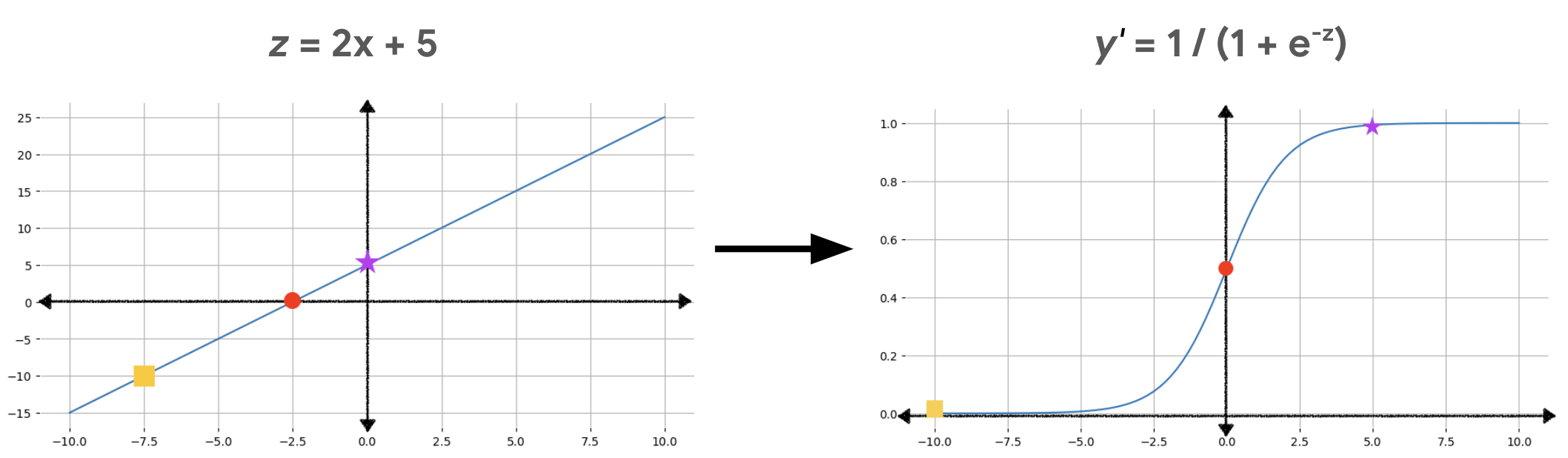
Dans la figure 2, une équation linéaire devient une entrée de la fonction sigmoïde, qui transforme la ligne droite en forme de S. Notez que l'équation linéaire peut générer des valeurs de z très grandes ou très petites, mais que la sortie de la fonction sigmoïde, y', est toujours comprise entre 0 et 1 (exclusivement). Par exemple, le carré jaune du graphique de gauche a une valeur z de -10, mais la fonction sigmoïde du graphique de droite mappe cette valeur -10 sur une valeur y' de 0,00004.

Exercice : Vérifier que vous avez bien compris

Un modèle de régression logistique avec trois caractéristiques présente les biais et pondérations suivants :

\[\begin{align} b &= 1 \\ w_1 &= 2 \\ w_2 &= -1 \\ w_3 &= 5 \end{align} \]

Prenons les valeurs d'entrée suivantes :

\[\begin{align} x_1 &= 0 \\ x_2 &= 10 \\ x_3 &= 2 \end{align} \]

Répondez aux deux questions suivantes.

1. Quelle est la valeur de z pour ces valeurs d'entrée ?

–1

0

0.731

1

Bonne réponse ! L'équation linéaire définie par les pondérations et le biais est la suivante : z = 1 + 2x₁ – x₂ + 5x₃. En insérant les valeurs d'entrée dans l'équation, on obtient z = 1 + (2)(0) - (10) + (5)(2) = 1.

2. Quelle est la prédiction de régression logistique pour ces valeurs d'entrée ?

0,268

0,5

0.731

Comme calculé dans le point 1 ci-dessus, le logit pour les valeurs d'entrée est de 1. En insérant cette valeur pour z dans la fonction sigmoïde :

\(y = \frac{1}{1 + e^{-z}} = \frac{1}{1 + e^{-1}} = \frac{1}{1 + 0.367} = \frac{1}{1.367} = 0.731\)

1

N'oubliez pas que le résultat de la fonction sigmoïde sera toujours supérieur à 0 et inférieur à 1.

Termes clés

• Classification binaire
• Logit
• Régression logistique
• Fonction sigmoïde