تتطلّب العديد من المشاكل تقديرًا للاحتمالية كمخرجات. الانحدار اللوجستي هو آلية فعّالة للغاية لحساب الاحتمالات. من الناحية العملية، يمكنك استخدام الاحتمالية التي تم إرجاعها بإحدى الطريقتين التاليتين:
تم تطبيقها "كما هي". على سبيل المثال، إذا كان نموذج توقّع الرسائل غير المرغوب فيها يتلقّى رسالة إلكترونية كمدخل ويُخرج القيمة
0.932، يشير ذلك إلى احتمال93.2%بأنّ الرسالة الإلكترونية هي رسالة غير مرغوب فيها.تم تحويلها إلى فئة ثنائية مثل
TrueأوFalse، أوSpamأوNot Spam.
تركّز هذه الوحدة على استخدام ناتج نموذج الانحدار اللوجستي كما هو. في وحدة التصنيف، ستتعرّف على كيفية تحويل هذا الناتج إلى فئة ثنائية.
الدالّة الإسية
قد تتساءل عن كيفية ضمان نموذج الانحدار اللوجستي أن يمثّل الناتج احتمالاً، وأن يقدّم دائمًا قيمة بين 0 و1. لحسن الحظ، هناك مجموعة من الدوال تُعرف باسم الدوال اللوجستية، ويحمل ناتجها الخصائص نفسها. تتضمّن الدالة اللوجستية القياسية، المعروفة أيضًا باسم الدالة السينية (sigmoid تعني "على شكل حرف S")، الصيغة التالية:
\[f(x) = \frac{1}{1 + e^{-x}}\]
where:
- f(x) هو ناتج الدالة السينية.
- e هو عدد أويلر: ثابت رياضي ≈ 2.71828.
- x هو الإدخال في الدالة السينية.
يوضّح الشكل 1 الرسم البياني المقابل للدالة السينية.
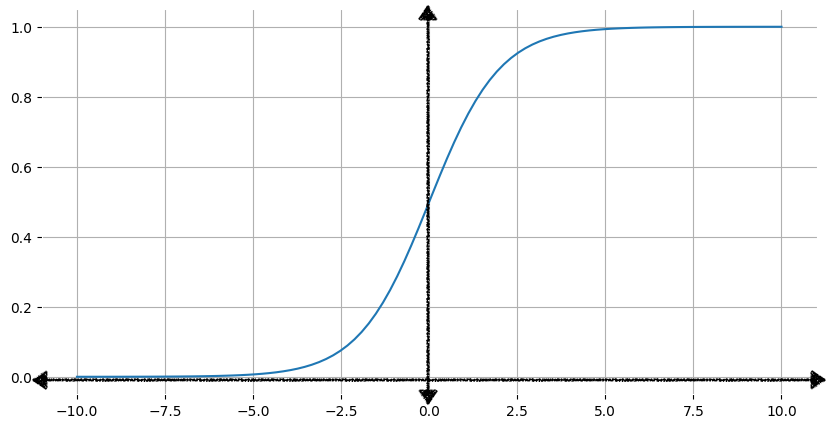
كلما زادت قيمة الإدخال، x، اقترب ناتج الدالة السينية من
1 ولكنّه لا يصل إليه أبدًا. وبالمثل، كلما انخفضت قيمة الإدخال، يقترب ناتج الدالة السينية من 0 ولكن لا يصل إليه أبدًا.
انقر هنا للحصول على شرح تفصيلي حول العمليات الحسابية التي تستند إليها الدالة السينية
يعرض الجدول أدناه قيم الناتج للدالة السينية لقيم الإدخال في النطاق من -7 إلى 7. لاحظ مدى سرعة اقتراب الدالة السينية من 0 عند انخفاض قيم الإدخال السالبة، ومدى سرعة اقتراب الدالة السينية من 1 عند ارتفاع قيم الإدخال الموجبة.
ومع ذلك، بغض النظر عن حجم قيمة الإدخال، سيكون الناتج دائمًا أكبر من 0 وأقل من 1.
| الإدخال | الناتج الإسّي |
|---|---|
| -7 | 0.001 |
| -6 | 0.002 |
| -5 | 0.007 |
| -4 | 0.018 |
| -3 | 0.047 |
| -2 | 0.119 |
| -1 | 0.269 |
| 0 | 0.50 |
| 1 | 0.731 |
| 2 | 0.881 |
| 3 | 0.952 |
| 4 | 0.982 |
| 5 | 0.993 |
| 6 | 0.997 |
| 7 | 0.999 |
تحويل الناتج الخطي باستخدام الدالة السينية
تمثّل المعادلة التالية المكوّن الخطي لنموذج الانحدار اللوجستي:
\[z = b + w_1x_1 + w_2x_2 + \ldots + w_Nx_N\]
where:
- z هو ناتج المعادلة الخطية، ويُعرف أيضًا باسم نسبة الاحتمالات اللوغاريتمية.
- b هو الانحياز.
- قيم w هي الأوزان التي تعلّمها النموذج.
- قيم x هي قيم الميزات لمثال معيّن.
للحصول على نتيجة الانحدار اللوجستي، يتم تمرير قيمة z إلى الدالة السينية، ما يؤدي إلى الحصول على قيمة (احتمالية) بين 0 و1:
\[y' = \frac{1}{1 + e^{-z}}\]
where:
- y' هو ناتج نموذج الانحدار اللوجستي.
- e هو عدد أويلر: ثابت رياضي ≈ 2.71828.
- z هو الناتج الخطي (كما هو محسوب في المعادلة السابقة).
مزيد من المعلومات حول مقياس لوغاريتم الاحتمالات
في المعادلة $z = b + w_1x_1 + w_2x_2 + \ldots + w_Nx_N$، يُشار إلى z على أنّه نسبة الاحتمالات اللوغاريتمية لأنّه إذا بدأت بالدالة السينية التالية (حيث $y$ هي ناتج نموذج الانحدار اللوجستي، وتمثّل احتمالاً):
$$y = \frac{1}{1 + e^{-z}}$$
ثم حلّ المعادلة لإيجاد قيمة z:
$$ z = \ln\left(\frac{y}{1-y}\right) $$
بعد ذلك، يتم تعريف z على أنّه اللوغاريتم الطبيعي لنسبة احتمالات النتيجتين المحتملتين: y و1 – y.
يوضّح الشكل 2 كيف يتم تحويل الناتج الخطي إلى ناتج الانحدار اللوجستي باستخدام هذه العمليات الحسابية.
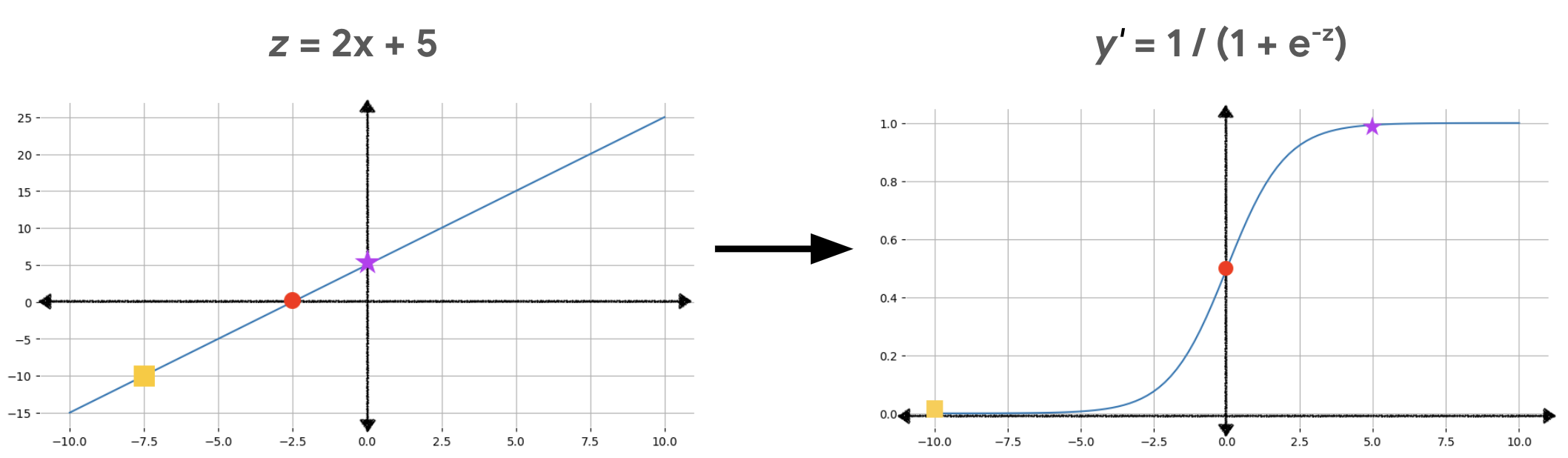
في الشكل 2، تصبح المعادلة الخطية مدخلاً للدالة السينية، التي تحوّل الخط المستقيم إلى شكل حرف S. لاحظ أنّ المعادلة الخطية يمكن أن تنتج قيمًا كبيرة جدًا أو صغيرة جدًا لـ z، ولكن ناتج الدالة السينية، y'، يكون دائمًا بين 0 و1، باستثناء هذين الرقمين. على سبيل المثال، المربّع الأصفر في الرسم البياني الأيسر لديه قيمة z تساوي -10، ولكن الدالة السينية في الرسم البياني الأيمن تحوّل القيمة -10 إلى قيمة y' تساوي 0.00004.
تمرين: التحقّق من فهمك
يحتوي نموذج الانحدار اللوجستي الذي يتضمّن ثلاث ميزات على التحيز والأوزان التالية:
\[\begin{align} b &= 1 \\ w_1 &= 2 \\ w_2 &= -1 \\ w_3 &= 5 \end{align} \]
بافتراض قيم الإدخال التالية:
\[\begin{align} x_1 &= 0 \\ x_2 &= 10 \\ x_3 &= 2 \end{align} \]
أجب عن السؤالَين التاليَين.
كما هو محسوب في النقطة 1 أعلاه، فإنّ نسبة الاحتمالات اللوغاريتمية لقيم الإدخال هي 1. إدخال هذه القيمة في z في الدالة السينية:
\(y = \frac{1}{1 + e^{-z}} = \frac{1}{1 + e^{-1}} = \frac{1}{1 + 0.367} = \frac{1}{1.367} = 0.731\)