הרבה בעיות דורשות הערכת הסתברות כפלט. רגרסיה לוגיסטית היא מנגנון יעיל במיוחד לחישוב הסתברויות. מבחינה מעשית, אפשר להשתמש בהסתברות שהוחזרה באחת משתי הדרכים הבאות:
הוחל 'כמו שהוא'. לדוגמה, אם מודל לחיזוי ספאם מקבל אימייל כקלט ומחזיר ערך של
0.932, המשמעות היא שההסתברות שהאימייל הוא ספאם היא93.2%.הפונקציה ממירה לקטגוריה בינארית, כמו
TrueאוFalse,SpamאוNot Spam.
המודול הזה מתמקד בשימוש בפלט של מודל רגרסיה לוגיסטית כמו שהוא. במודול הסיווג תלמדו איך להמיר את הפלט הזה לקטגוריה בינארית.
פונקציית סיגמואיד
יכול להיות שאתם תוהים איך מודל רגרסיה לוגיסטית יכול להבטיח שהפלט שלו ייצג הסתברות, ושתמיד יוחזר ערך בין 0 ל-1. במקרה, יש משפחה של פונקציות שנקראות פונקציות לוגיסטיות שהפלט שלהן כולל את אותן תכונות. הפונקציה הלוגיסטית הסטנדרטית, שנקראת גם פונקציית סיגמואיד (sigmoid פירושו 'בצורת S'), מוגדרת בנוסחה הבאה:
\[f(x) = \frac{1}{1 + e^{-x}}\]
where:
- f(x) הוא הפלט של פונקציית הסיגמואיד.
- e הוא מספר אוילר: קבוע מתמטי ≈ 2.71828.
- x הוא הקלט לפונקציית הסיגמואיד.
איור 1 מציג את הגרף המתאים של פונקציית הסיגמואיד.
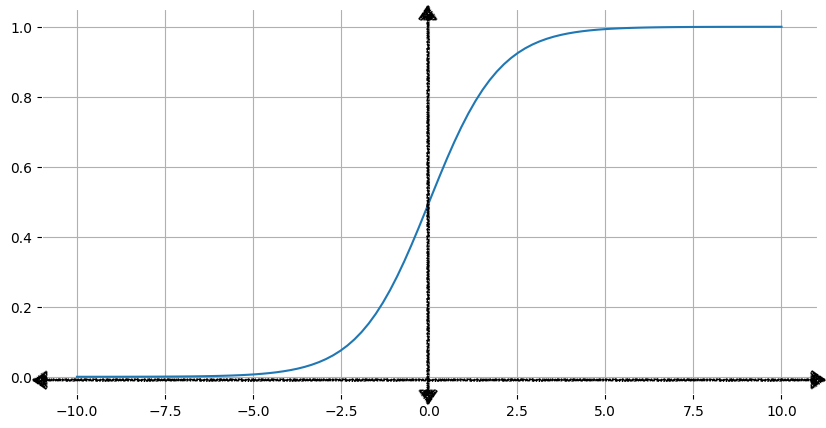
ככל שהקלט, x, גדל, הפלט של פונקציית הסיגמואיד מתקרב ל-0, אבל אף פעם לא מגיע ל-0.1 באופן דומה, כשהקלט קטן יותר, הפלט של פונקציית הסיגמואיד מתקרב ל-0 אבל אף פעם לא מגיע אליו.
כאן אפשר לקרוא ניתוח מעמיק של המתמטיקה שמאחורי פונקציית הסיגמואיד
בטבלה הבאה מוצגים ערכי הפלט של פונקציית הסיגמואיד עבור ערכי קלט בטווח -7 עד 7. שימו לב כמה מהר הסיגמואיד מתקרב ל-0 כשערכי הקלט השליליים יורדים, וכמה מהר הסיגמואיד מתקרב ל-1 כשערכי הקלט החיוביים עולים.
עם זאת, לא משנה כמה גדול או קטן ערך הקלט, הפלט תמיד יהיה גדול מ-0 וקטן מ-1.
| קלט | פלט סיגמואידי |
|---|---|
| -7 | 0.001 |
| -6 | 0.002 |
| -5 | 0.007 |
| -4 | 0.018 |
| -3 | 0.047 |
| -2 | 0.119 |
| -1 | 0.269 |
| 0 | 0.50 |
| 1 | 0.731 |
| 2 | 0.881 |
| 3 | 0.952 |
| 4 | 0.982 |
| 5 | 0.993 |
| 6 | 0.997 |
| 7 | 0.999 |
שינוי פלט ליניארי באמצעות פונקציית הסיגמואיד
המשוואה הבאה מייצגת את הרכיב הלינארי של מודל רגרסיה לוגיסטית:
\[z = b + w_1x_1 + w_2x_2 + \ldots + w_Nx_N\]
where:
- z הוא הפלט של המשוואה הלינארית, שנקרא גם הלוג של הסיכויים.
- b היא ההטיה.
- הערכים של w הם המשקלים שהמודל למד.
- הערכים x הם ערכי התכונות של דוגמה מסוימת.
כדי לקבל את התחזית של הרגרסיה הלוגיסטית, מעבירים את הערך z לפונקציית הסיגמואיד, ומקבלים ערך (הסתברות) בין 0 ל-1:
\[y' = \frac{1}{1 + e^{-z}}\]
where:
- y' הוא הפלט של מודל הרגרסיה הלוגיסטית.
- e הוא מספר אוילר: קבוע מתמטי ≈ 2.71828.
- z הוא הפלט הלינארי (כפי שמחושב במשוואה הקודמת).
מידע נוסף על יחסי הסתברות
במשוואה $z = b + w_1x_1 + w_2x_2 + \ldots + w_Nx_N$, z נקרא הלוגיתם של הסיכויים, כי אם מתחילים עם פונקציית הסיגמואיד הבאה (כאשר $y$ הוא הפלט של מודל רגרסיה לוגיסטית, שמייצג הסתברות):
$$y = \frac{1}{1 + e^{-z}}$$
ואז פותרים את המשוואה כדי למצוא את z:
$$ z = \ln\left(\frac{y}{1-y}\right) $$
אז z מוגדר כלוגריתם הטבעי של היחס בין ההסתברויות של שתי התוצאות האפשריות: y ו-1 – y.
איור 2 מראה איך פלט לינארי הופך לפלט של רגרסיה לוגיסטית באמצעות החישובים האלה.
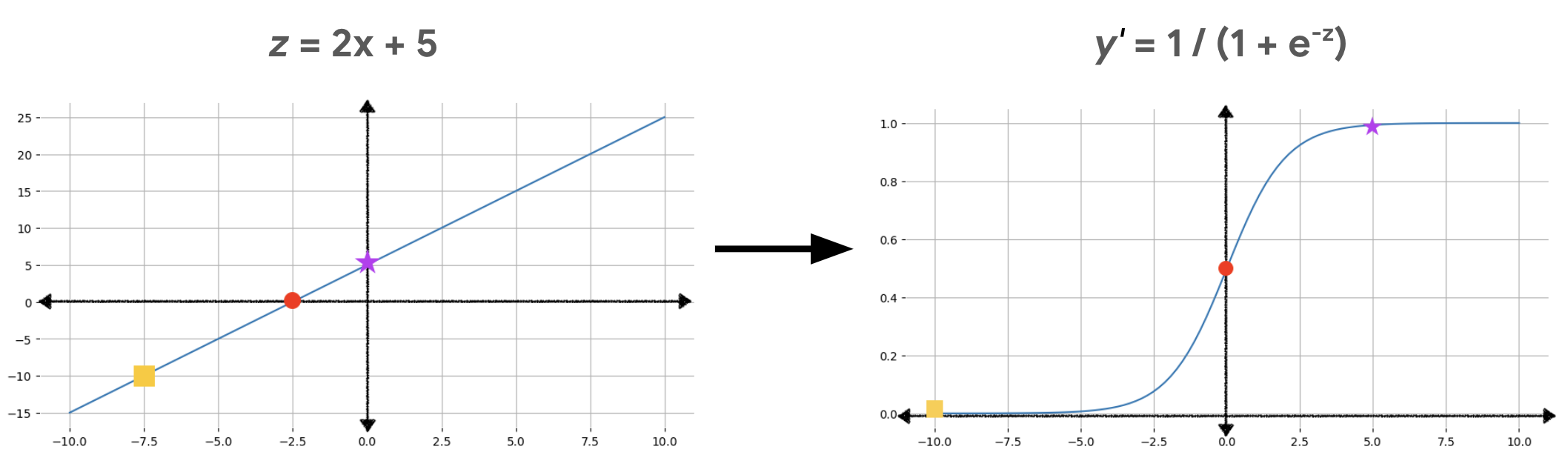
באיור 2, משוואה לינארית הופכת לקלט של פונקציית הסיגמואיד, שמעקמת את הקו הישר לצורת S. שימו לב שהמשוואה הלינארית יכולה להפיק ערכים גדולים מאוד או קטנים מאוד של z, אבל הפלט של פונקציית הסיגמואיד, y', הוא תמיד בין 0 ל-1, לא כולל. לדוגמה, לריבוע הצהוב בתרשים הימני יש ערך z של -10, אבל פונקציית הסיגמואיד בתרשים השמאלי ממפה את הערך -10 לערך y' של 0.00004.
תרגיל: בדיקת ההבנה
מודל רגרסיה לוגיסטית עם שלושה מאפיינים כולל את ההטיה והמשקלים הבאים:
\[\begin{align} b &= 1 \\ w_1 &= 2 \\ w_2 &= -1 \\ w_3 &= 5 \end{align} \]
בהינתן ערכי הקלט הבאים:
\[\begin{align} x_1 &= 0 \\ x_2 &= 10 \\ x_3 &= 2 \end{align} \]
עליך לענות על שתי השאלות הבאות.
כפי שחושב בסעיף 1 למעלה, הלוג-אודס של ערכי הקלט הוא 1. מציבים את הערך הזה של z בפונקציית הסיגמואיד:
\(y = \frac{1}{1 + e^{-z}} = \frac{1}{1 + e^{-1}} = \frac{1}{1 + 0.367} = \frac{1}{1.367} = 0.731\)
