Bu modülde doğrusal regresyon kavramları tanıtılmaktadır.
'nı inceleyin.Doğrusal regresyon, ve değişkenler arasındaki ilişkiyi bulmak için kullanılan istatistiksel tekniktir. Makine öğreniminde doğrusal regresyon, yeni model ile features ve etiket ekleyin.
Örneğin, bir arabanın yakıt verimliliğini her gün mil cinsinden tahmin etmek istediğimizi varsayalım. 2, 5 litre galon tasarruf ediyor. Şu veri kümesi elimizde mevcut:
| 1.000 sterlin (özellik) | Mil/galon (etiket) |
|---|---|
| 3,5 | 18 |
| 3,69 | 15 |
| 3,44 | 18 |
| 3,43 | 16 |
| 4,34 | 15 |
| 4,42 | 14 |
| 2,37 | 24 |
Bu noktaları çizseydik aşağıdaki grafiği elde ederdik:
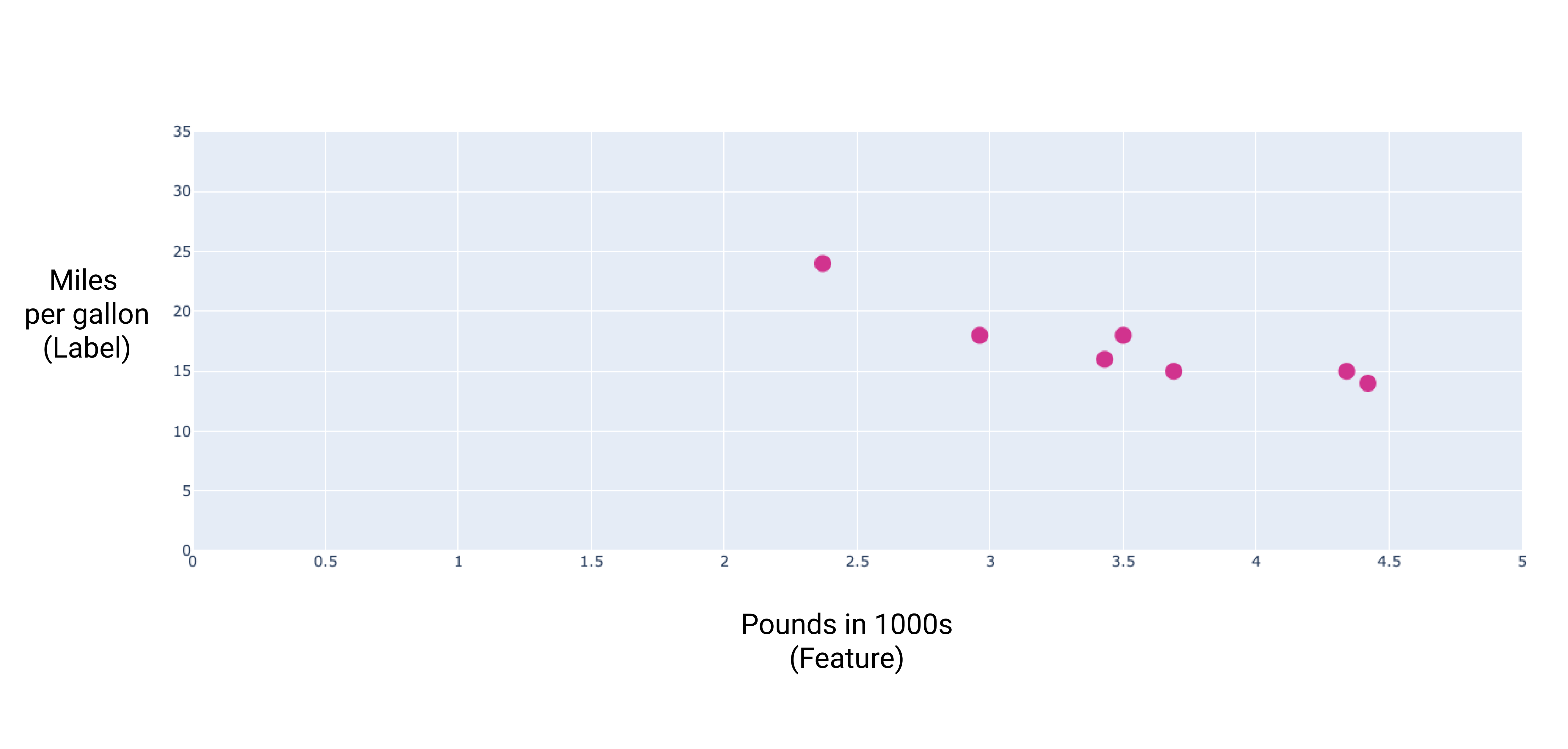
Şekil 1. Araç ağırlığı (libre cinsinden) ve galon başına mil cinsinden karşılaştırma. Kullanıcı araba ağırlaşır, litre başına mil başına düşen derece genellikle düşer.
Noktalar arasından en uygun çizgiyi çizerek kendi modelimizi oluşturabiliriz:
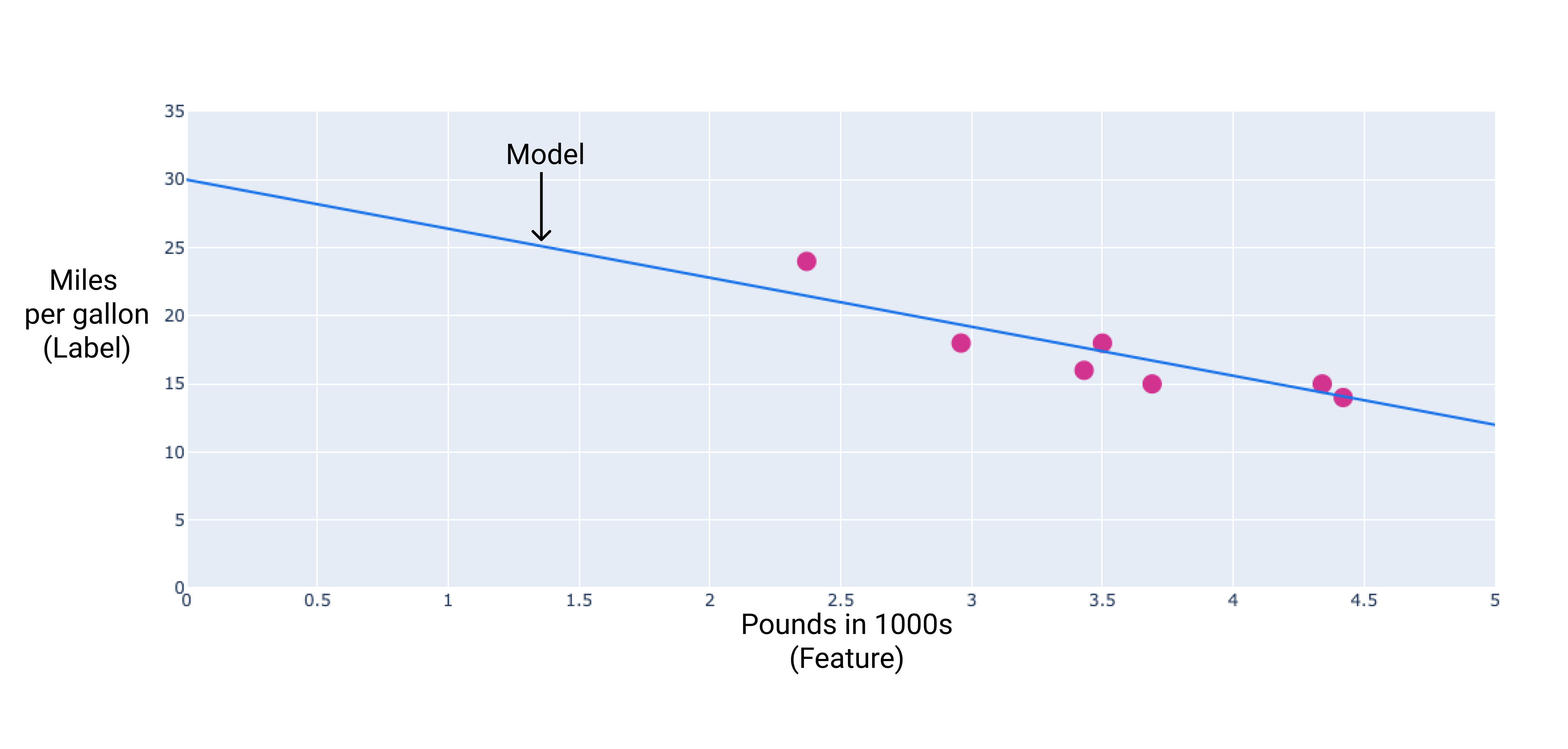
2. Şekil. Önceki şekilde bulunan verilerin arasından çizilen en uygun çizgi.
Doğrusal regresyon denklemi
Cebirsel terimlerde model, $ y = mx + b $ şeklinde tanımlanır. Burada
- TL y $, tahmin etmek istediğimiz değer olan litre başına mildir.
- $ m $, çizginin eğimidir.
- $ x $, İngiliz sterlini, yani girdi değerimizdir.
- $ b $ y kesim noktasıdır.
Makine öğreniminde bir doğrusal regresyon modelinin denklemini aşağıdaki gibi yazıyoruz:
Bu örnekte:
- yıl ABD doları $, tahmin edilen etikettir, yani çıktıdır.
- ₺ ₺ tarafsızdır belirler. Önyargı, cebirdeki y kesim noktası ile aynı kavramdır denklemini ifade eder. Makine öğreniminde yanlılık bazen $ w_0 $ olarak ifade edilir. Yanlı olma modelin bir parametresi eğitim sırasında hesaplanır.
- $ w_1 $, şu öğenin ağırlığıdır: özelliğini kullanabilirsiniz. Ağırlık, cebirdeki eğim $ m $ ile aynı kavramdır denklemini ifade eder. Ağırlık: parametresi hesaplanan miktardır.
- x_1 ABD doları bir özelliktir. giriş.
Model, eğitim sırasında en iyi sonucu veren ağırlığı ve yanlılığı hesaplar modeli.
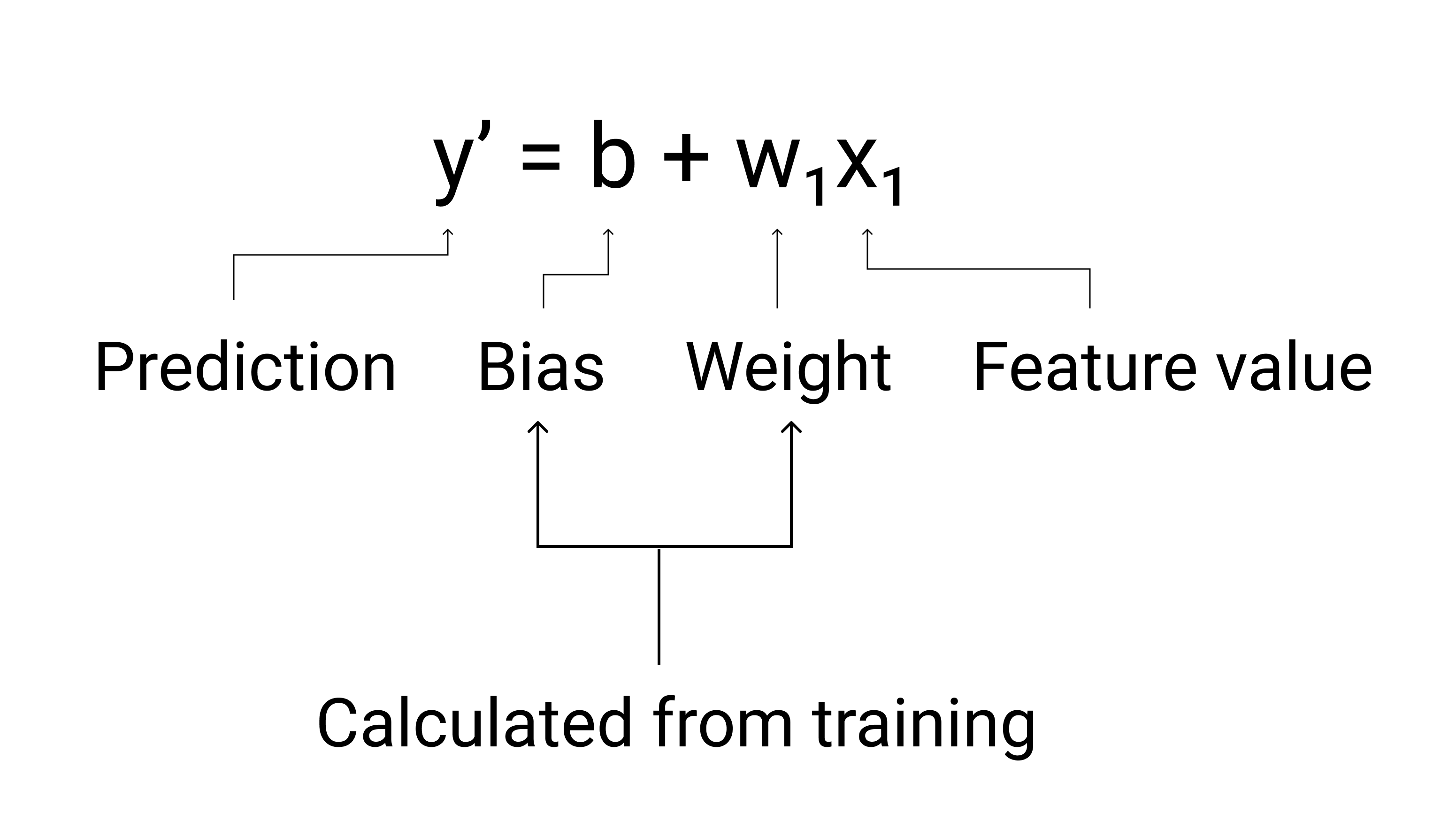
3. Şekil. Doğrusal bir modelin matematiksel gösterimi.
Örneğimizde, ağırlığı ve sapmayı çizdiğimiz çizgiye göre hesaplarız. İlgili içeriği oluşturmak için kullanılan önyargı 30'dur (çizginin y ekseniyle kesiştiği yerde) ve ağırlık -3,6'dır (çizginin y ekseniyle kesiştiği yerde) çizginin eğimi) girin. Model $ y' şeklinde tanımlanır = 30 + (-3, 6)(x_1) $ ve tahminde bulunmak için kullanabiliriz. Örneğin, bu modeli kullanarak 1.000 kiloluk bir arabanın tahmini yakıt verimliliği saatte 25,6 mil olacaktır galon.
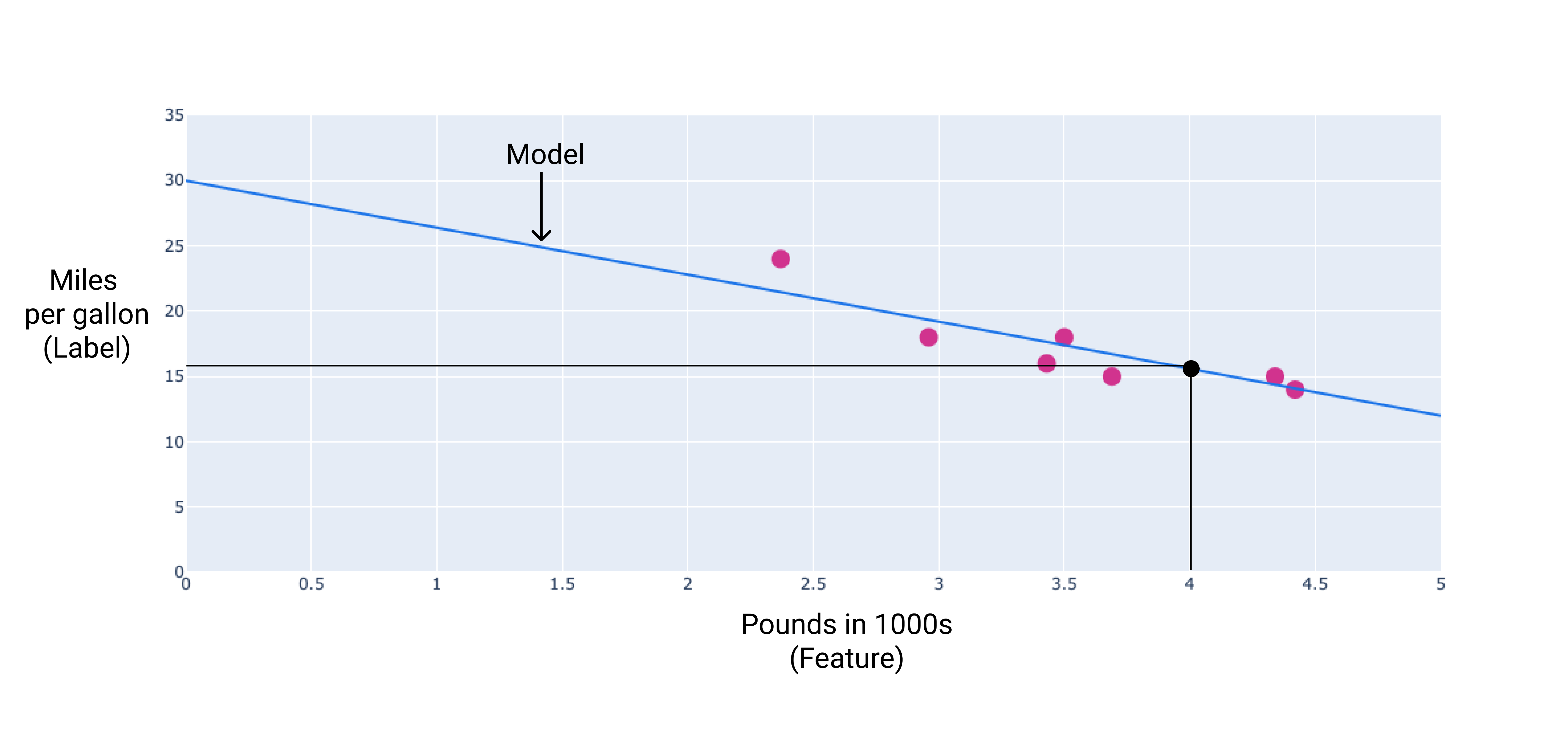
4. Şekil. Bu modele göre, 4.000 kiloluk bir arabanın tahmini litre başına 25,2 kilometre yakıt verimliliği.
Birden çok özelliğe sahip modeller
Bu bölümdeki örnekte yalnızca tek bir özellik kullanılıyor olsa da: sahip olabilir. Daha sofistike bir model ise birden fazla özelliğe, her birinin ayrı bir ağırlığı vardır ($ w_1 $, $ w_2 $ vb.). Örneğin, bir model temel alan aşağıdaki gibi yazılır:
yıl ABD doları = b + w_1x_1 + w_2x_2 + w_3x_3 + w_4x_4 + w_5x_5 ABD doları
Örneğin, yakıt tüketimini tahmin eden bir model, Örneğin:
- Motor deplasmanı
- İvme
- Silindir sayısı
- Beygir gücü
Bu model aşağıdaki gibi yazılır:
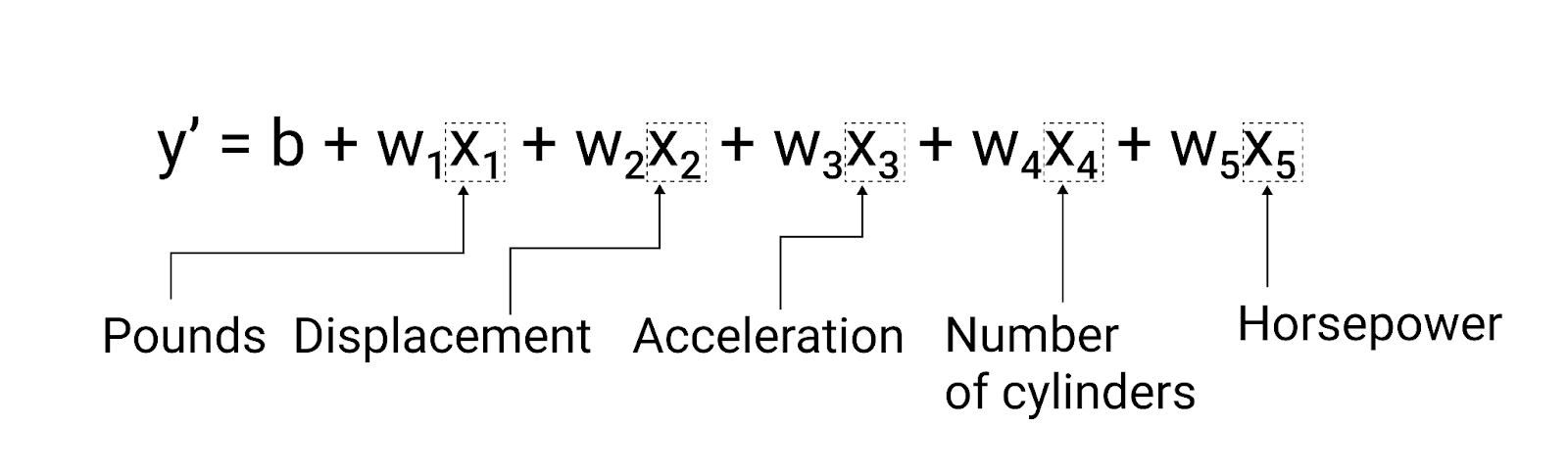
5. Şekil. Bir arabanın galon başına düşen mesafeyi tahmin etmek için beş özelliğe sahip bir model puan.
Bu ek özelliklerden bazılarının grafiğini çizerek daha iyi bir performansa sahip olduklarını etiketle doğrusal ilişki, mil/galon:
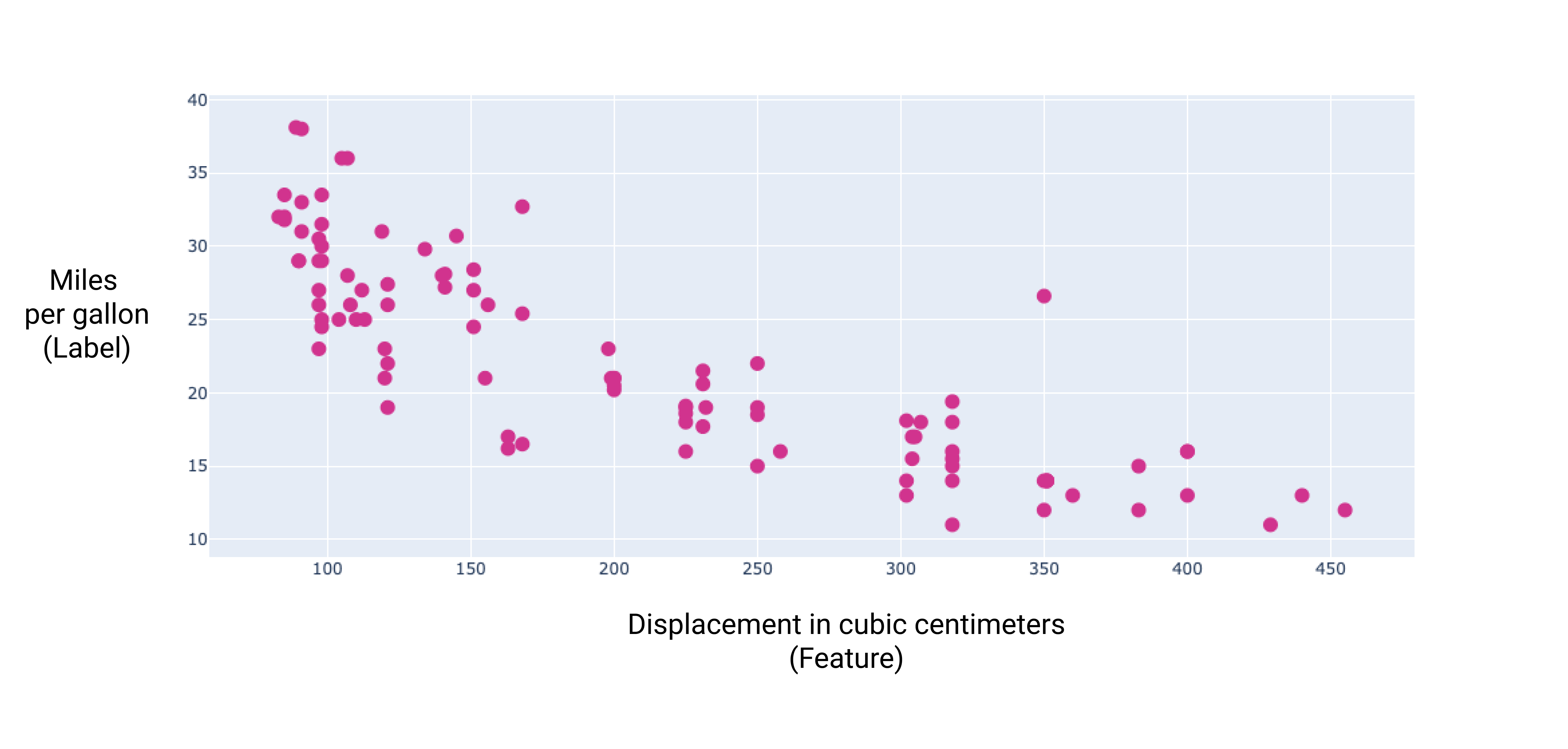
6. Şekil. Bir arabanın santimetre küp cinsinden yer değiştirme ve galon başına mil puan. Bir arabanın motoru büyüdükçe, genellikle galon başına mil oranı azalıyor.
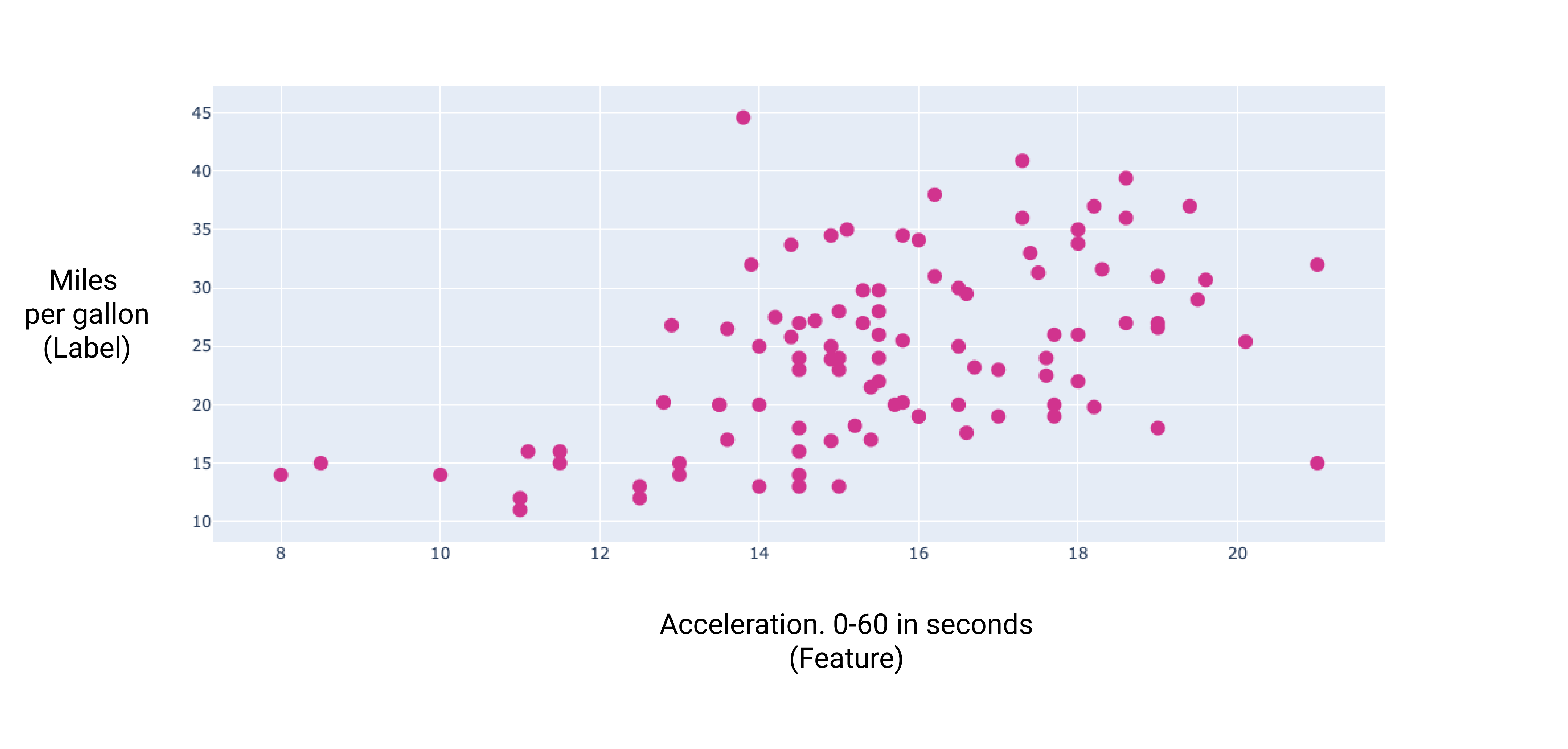
7. Şekil. Bir arabanın ivmesi ve galon başına mil sayısı. Arabanın hızlanma daha uzun sürer, litre başına mil sayısı genellikle artar.
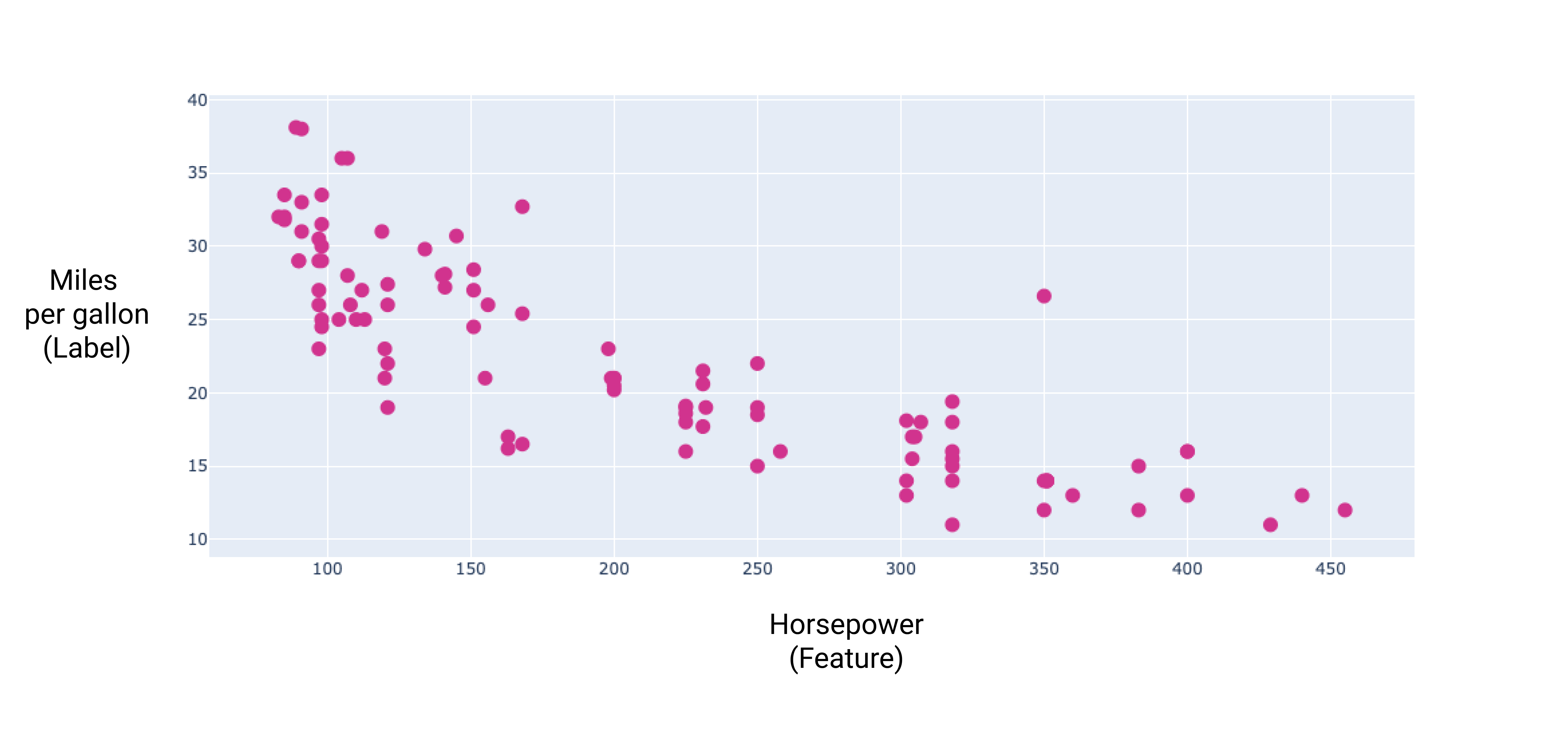
8. Şekil. Bir arabanın beygir gücü ve galon başına mil sayısı. Arabanın beygir gücü artarken, galon başına mil değeri genellikle azalır.
