এই মডিউলটি রৈখিক রিগ্রেশন ধারণা প্রবর্তন করে।
লিনিয়ার রিগ্রেশন হল একটি পরিসংখ্যানগত কৌশল যা ভেরিয়েবলের মধ্যে সম্পর্ক খুঁজে বের করতে ব্যবহৃত হয়। একটি ML প্রসঙ্গে, লিনিয়ার রিগ্রেশন বৈশিষ্ট্য এবং একটি লেবেলের মধ্যে সম্পর্ক খুঁজে পায়।
উদাহরণস্বরূপ, ধরুন গাড়িটি কতটা ভারী তার উপর ভিত্তি করে আমরা গ্যালন প্রতি মাইলে একটি গাড়ির জ্বালানি দক্ষতার পূর্বাভাস দিতে চাই এবং আমাদের কাছে নিম্নলিখিত ডেটাসেট রয়েছে:
| পাউন্ড ইন 1000 (বৈশিষ্ট্য) | মাইলস প্রতি গ্যালন (লেবেল) |
|---|---|
| 3.5 | 18 |
| 3.69 | 15 |
| 3.44 | 18 |
| 3.43 | 16 |
| ৪.৩৪ | 15 |
| ৪.৪২ | 14 |
| 2.37 | 24 |
যদি আমরা এই পয়েন্টগুলি প্লট করি, আমরা নিম্নলিখিত গ্রাফটি পেতে পারি:
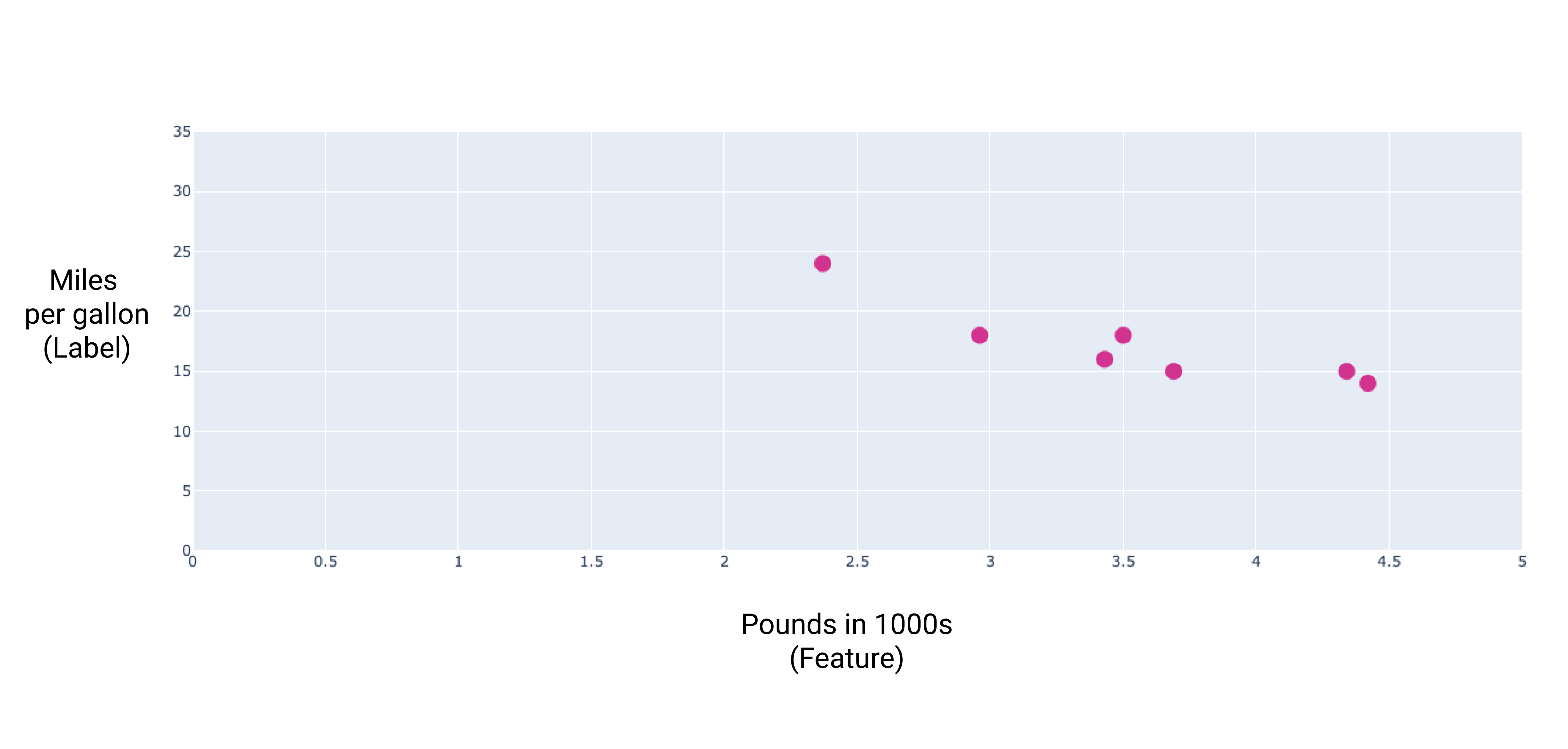
চিত্র 1 । গাড়ির ভারীতা (পাউন্ডে) বনাম মাইল প্রতি গ্যালন রেটিং। একটি গাড়ি যত ভারী হয়, তার মাইল প্রতি গ্যালন রেটিং সাধারণত কমে যায়।
আমরা পয়েন্টগুলির মাধ্যমে একটি সেরা ফিট লাইন অঙ্কন করে আমাদের নিজস্ব মডেল তৈরি করতে পারি:
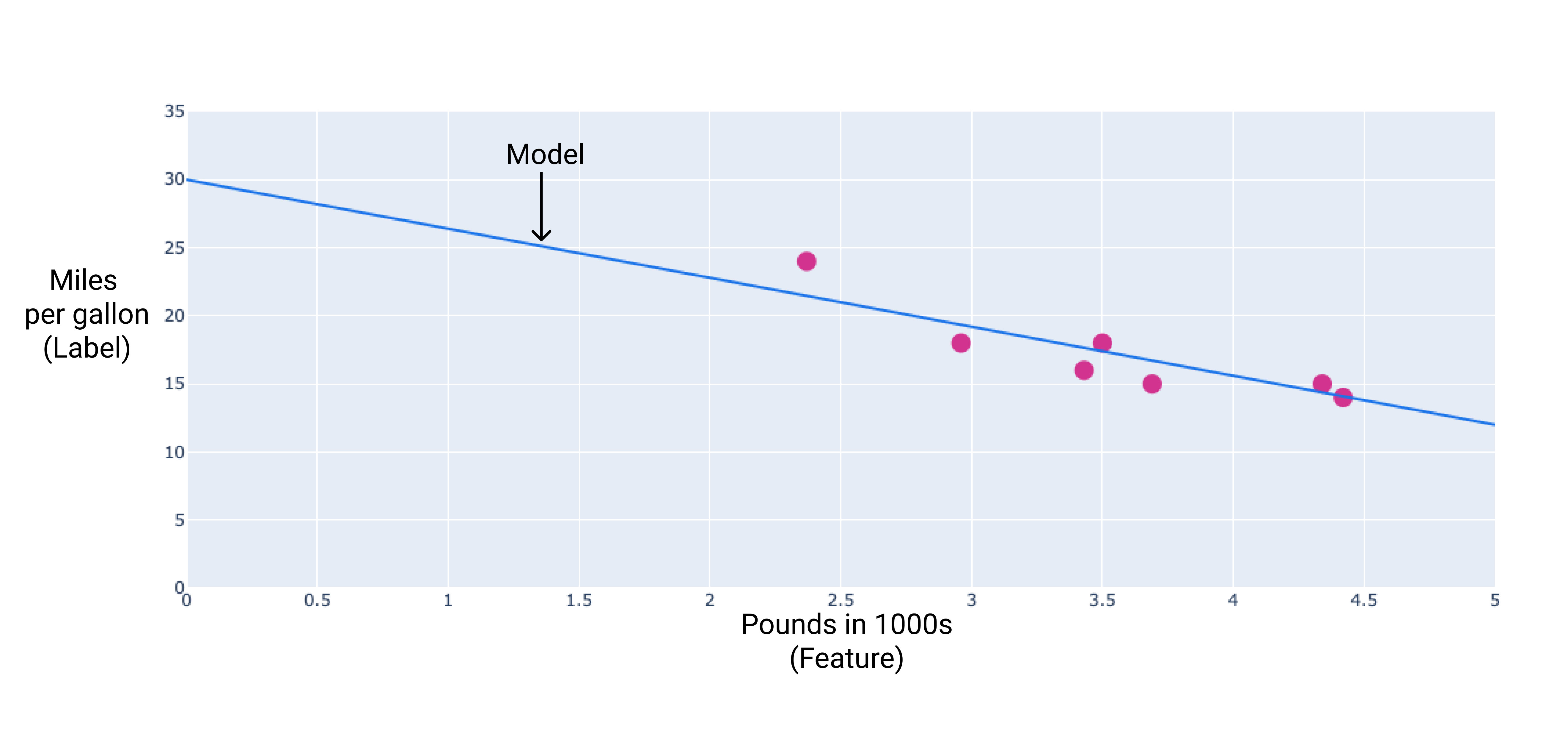
চিত্র 2 । পূর্ববর্তী চিত্র থেকে ডেটার মাধ্যমে আঁকা একটি সেরা ফিট লাইন।
রৈখিক রিগ্রেশন সমীকরণ
বীজগণিতের ভাষায়, মডেলটিকে $y = mx + b$ হিসাবে সংজ্ঞায়িত করা হবে, যেখানে
- $ y $ হল মাইল প্রতি গ্যালন- যে মান আমরা ভবিষ্যদ্বাণী করতে চাই।
- $m $ হল লাইনের ঢাল।
- $ x $ হল পাউন্ড—আমাদের ইনপুট মান।
- $b$ হল y-ইন্টারসেপ্ট।
এমএল-এ, আমরা একটি লিনিয়ার রিগ্রেশন মডেলের জন্য সমীকরণটি নিম্নরূপ লিখি:
কোথায়:
- $ y' $ হল পূর্বাভাসিত লেবেল—আউটপুট।
- $b$ হল মডেলের পক্ষপাত । বায়াস একটি লাইনের জন্য বীজগণিতীয় সমীকরণে y-ইন্টারসেপ্টের মতো একই ধারণা। ML-এ, পক্ষপাতকে কখনও কখনও $w_0 $ হিসাবে উল্লেখ করা হয়। বায়াস মডেলের একটি প্যারামিটার এবং প্রশিক্ষণের সময় গণনা করা হয়।
- $w_1 $ হল বৈশিষ্ট্যের ওজন । একটি লাইনের বীজগাণিতিক সমীকরণে ঢাল $m $ হিসাবে ওজন একই ধারণা। ওজন মডেলের একটি প্যারামিটার এবং প্রশিক্ষণের সময় গণনা করা হয়।
- $ x_1 $ হল একটি বৈশিষ্ট্য —ইনপুট।
প্রশিক্ষণের সময়, মডেলটি ওজন এবং পক্ষপাত গণনা করে যা সেরা মডেল তৈরি করে।
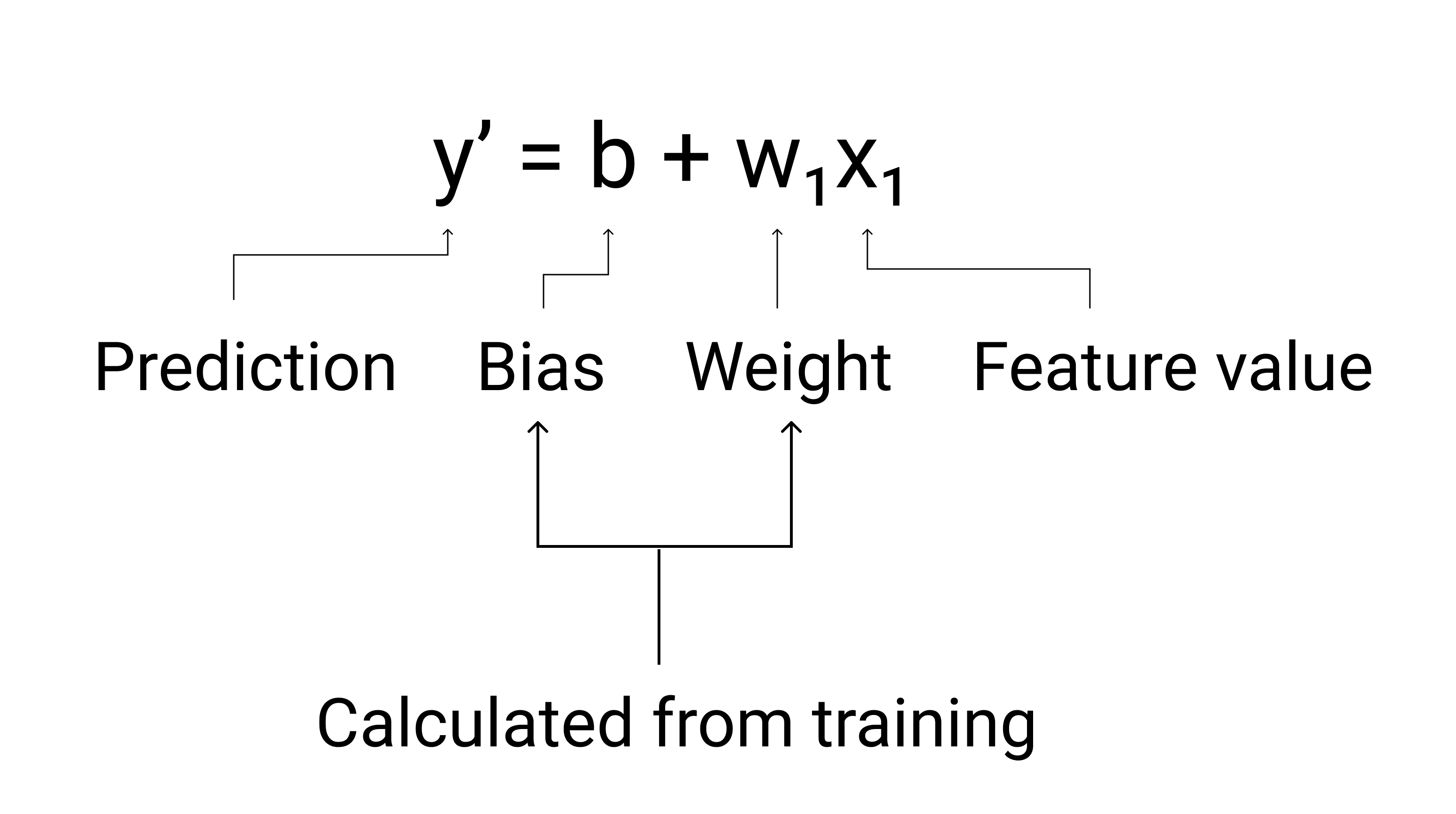
চিত্র 3 । একটি লিনিয়ার মডেলের গাণিতিক উপস্থাপনা।
আমাদের উদাহরণে, আমরা যে লাইনটি আঁকেছি তার থেকে আমরা ওজন এবং পক্ষপাত গণনা করব। পক্ষপাত 30 (যেখানে লাইনটি y-অক্ষকে ছেদ করে), এবং ওজন -3.6 (রেখার ঢাল)। মডেলটিকে $y' = 30 + (-3.6)(x_1) $ হিসাবে সংজ্ঞায়িত করা হবে এবং আমরা ভবিষ্যদ্বাণী করতে এটি ব্যবহার করতে পারি। উদাহরণস্বরূপ, এই মডেলটি ব্যবহার করে, একটি 4,000-পাউন্ড গাড়ির প্রতি গ্যালন 15.6 মাইল একটি পূর্বাভাসিত জ্বালানী দক্ষতা থাকবে।
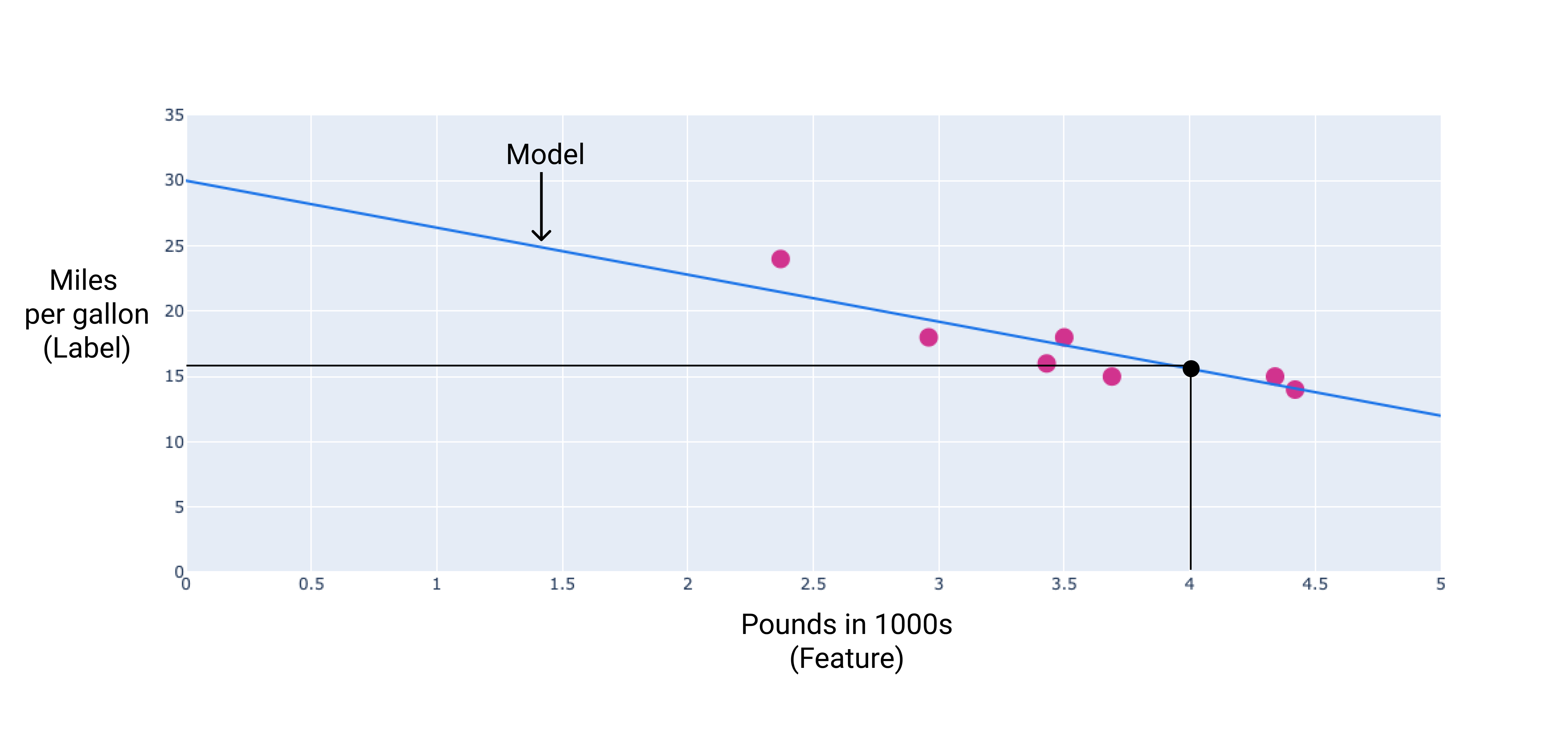
চিত্র 4 । মডেলটি ব্যবহার করে, একটি 4,000-পাউন্ড গাড়ির প্রতি গ্যালন 15.6 মাইল একটি পূর্বাভাসিত জ্বালানী দক্ষতা রয়েছে।
একাধিক বৈশিষ্ট্য সহ মডেল
যদিও এই বিভাগে উদাহরণটি শুধুমাত্র একটি বৈশিষ্ট্য ব্যবহার করে—গাড়ির ভারীতা—একটি আরও পরিশীলিত মডেল একাধিক বৈশিষ্ট্যের উপর নির্ভর করতে পারে, প্রতিটির আলাদা ওজন ($ w_1 $, $ w_2 $, ইত্যাদি)। উদাহরণস্বরূপ, একটি মডেল যা পাঁচটি বৈশিষ্ট্যের উপর নির্ভর করে তা নিম্নরূপ লেখা হবে:
$y' = b + w_1x_1 + w_2x_2 + w_3x_3 + w_4x_4 + w_5x_5 $
উদাহরণস্বরূপ, একটি মডেল যা গ্যাস মাইলেজের পূর্বাভাস দেয় অতিরিক্ত বৈশিষ্ট্যগুলি ব্যবহার করতে পারে যেমন:
- ইঞ্জিন স্থানচ্যুতি
- ত্বরণ
- সিলিন্ডারের সংখ্যা
- অশ্বশক্তি
এই মডেলটি নিম্নরূপ লেখা হবে:
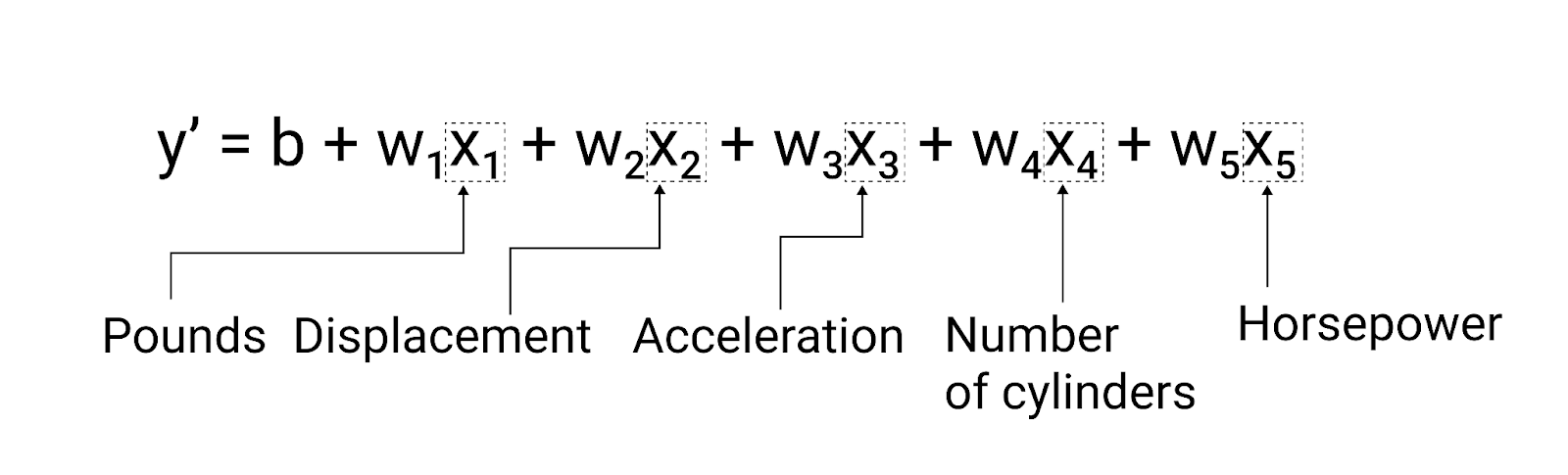
চিত্র 5 । গ্যালন রেটিং প্রতি একটি গাড়ির মাইল ভবিষ্যদ্বাণী করার জন্য পাঁচটি বৈশিষ্ট্য সহ একটি মডেল৷
এই অতিরিক্ত বৈশিষ্ট্যগুলির কিছু গ্রাফ করে, আমরা দেখতে পারি যে তাদের লেবেলের সাথে একটি রৈখিক সম্পর্ক রয়েছে, প্রতি গ্যালন মাইল:
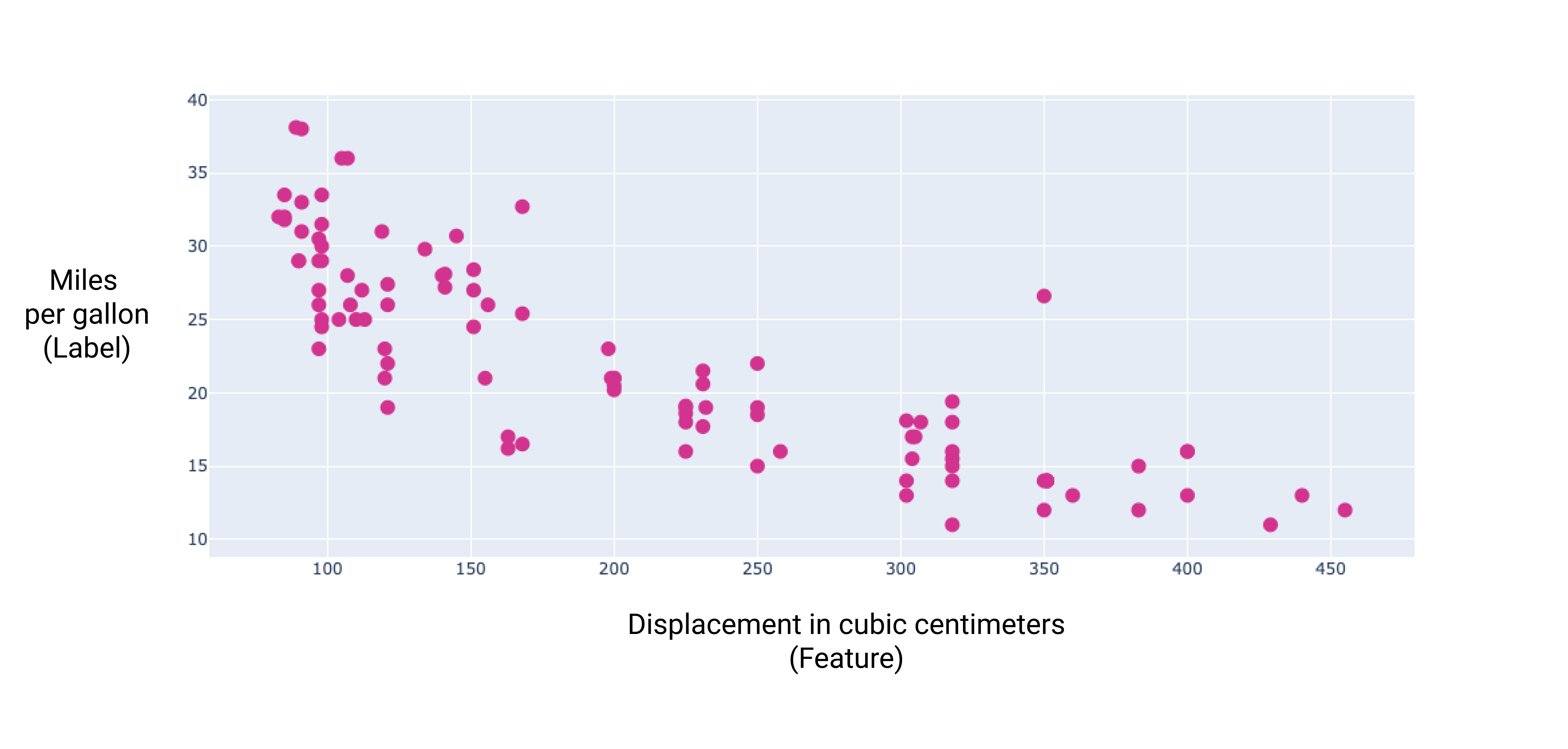
চিত্র 6 । কিউবিক সেন্টিমিটারে একটি গাড়ির স্থানচ্যুতি এবং প্রতি গ্যালন রেটিং এর মাইল। একটি গাড়ির ইঞ্জিন বড় হওয়ার সাথে সাথে এর মাইল প্রতি গ্যালন রেটিং সাধারণত হ্রাস পায়।
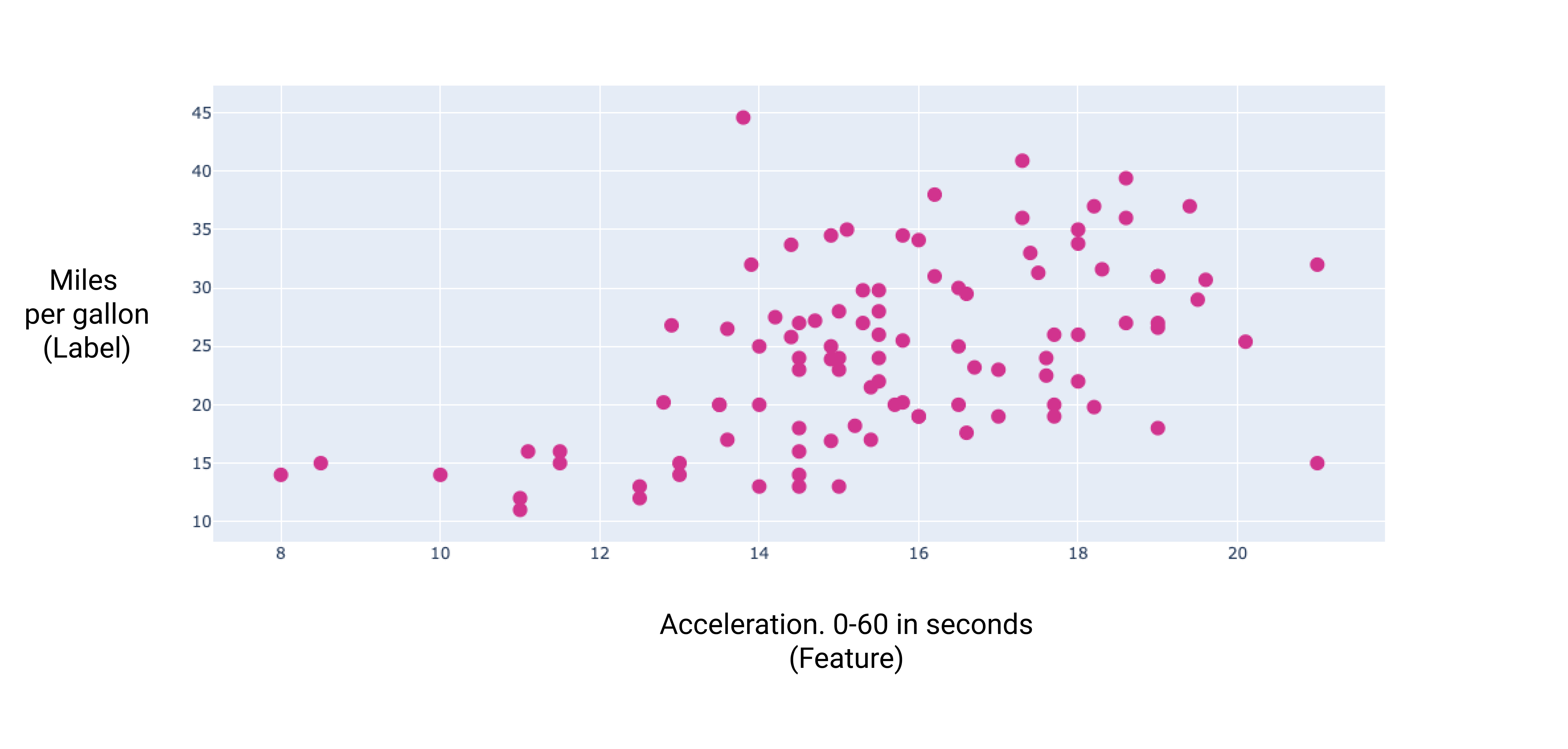
চিত্র 7 । একটি গাড়ির ত্বরণ এবং এর মাইল প্রতি গ্যালন রেটিং। যেহেতু একটি গাড়ির ত্বরণ বেশি সময় নেয়, তাই মাইল প্রতি গ্যালন রেটিং সাধারণত বৃদ্ধি পায়।
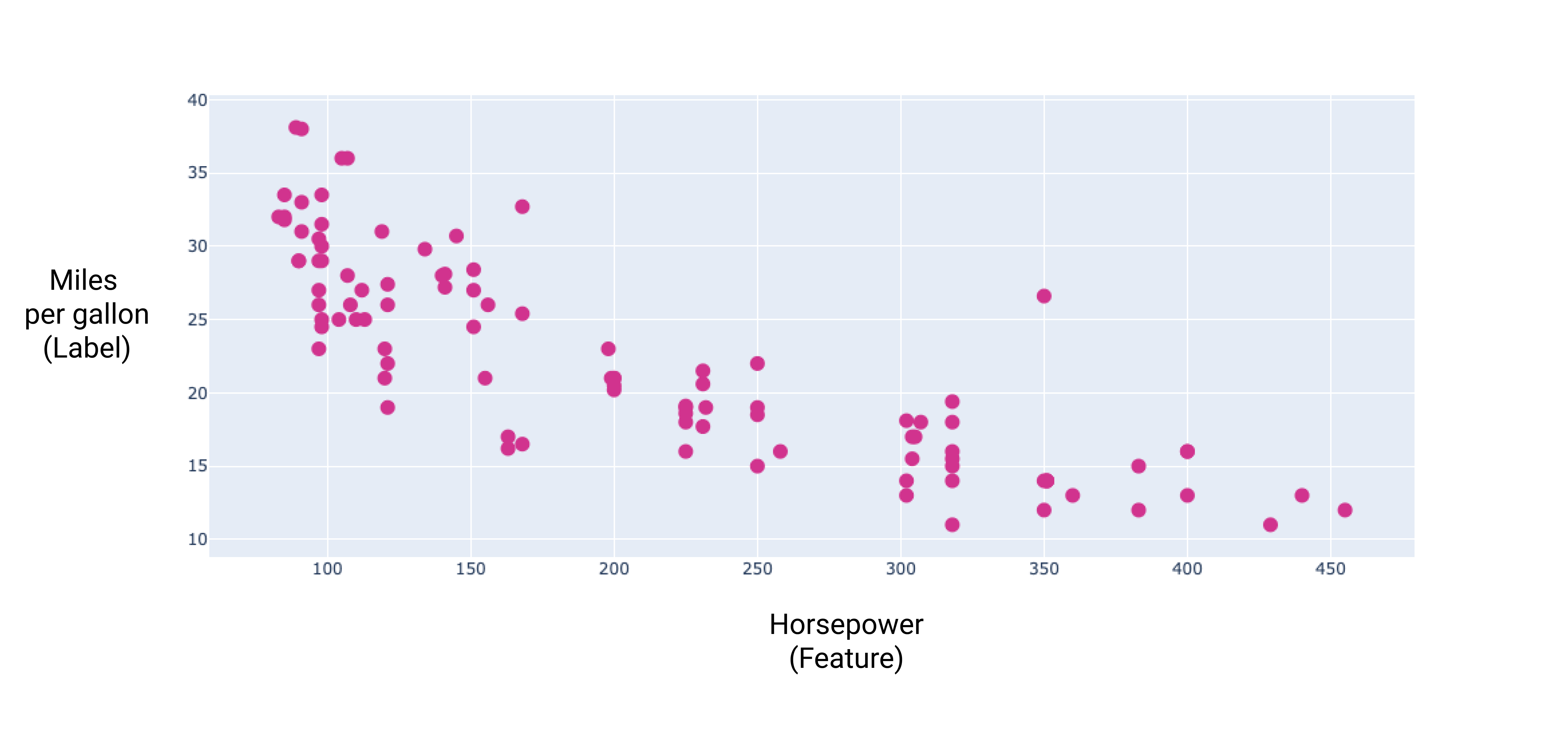
চিত্র 8 । একটি গাড়ির অশ্বশক্তি এবং এর মাইল প্রতি গ্যালন রেটিং। গাড়ির হর্সপাওয়ার বাড়ার সাথে সাথে মাইল প্রতি গ্যালন রেটিং সাধারণত কমে যায়।
অনুশীলন: আপনার বোঝার পরীক্ষা করুন
এই মডিউলটি রৈখিক রিগ্রেশন ধারণা প্রবর্তন করে।
লিনিয়ার রিগ্রেশন হল একটি পরিসংখ্যানগত কৌশল যা ভেরিয়েবলের মধ্যে সম্পর্ক খুঁজে বের করতে ব্যবহৃত হয়। একটি ML প্রসঙ্গে, লিনিয়ার রিগ্রেশন বৈশিষ্ট্য এবং একটি লেবেলের মধ্যে সম্পর্ক খুঁজে পায়।
উদাহরণস্বরূপ, ধরুন গাড়িটি কতটা ভারী তার উপর ভিত্তি করে আমরা গ্যালন প্রতি মাইলে একটি গাড়ির জ্বালানি দক্ষতার পূর্বাভাস দিতে চাই এবং আমাদের কাছে নিম্নলিখিত ডেটাসেট রয়েছে:
| পাউন্ড ইন 1000 (বৈশিষ্ট্য) | মাইলস প্রতি গ্যালন (লেবেল) |
|---|---|
| 3.5 | 18 |
| 3.69 | 15 |
| 3.44 | 18 |
| 3.43 | 16 |
| ৪.৩৪ | 15 |
| ৪.৪২ | 14 |
| 2.37 | 24 |
যদি আমরা এই পয়েন্টগুলি প্লট করি, আমরা নিম্নলিখিত গ্রাফটি পেতে পারি:

চিত্র 1 । গাড়ির ভারীতা (পাউন্ডে) বনাম মাইল প্রতি গ্যালন রেটিং। একটি গাড়ি যত ভারী হয়, তার মাইল প্রতি গ্যালন রেটিং সাধারণত কমে যায়।
আমরা পয়েন্টগুলির মাধ্যমে একটি সেরা ফিট লাইন অঙ্কন করে আমাদের নিজস্ব মডেল তৈরি করতে পারি:

চিত্র 2 । পূর্ববর্তী চিত্র থেকে ডেটার মাধ্যমে আঁকা একটি সেরা ফিট লাইন।
রৈখিক রিগ্রেশন সমীকরণ
বীজগণিতের ভাষায়, মডেলটিকে $y = mx + b$ হিসাবে সংজ্ঞায়িত করা হবে, যেখানে
- $ y $ হল মাইল প্রতি গ্যালন- যে মান আমরা ভবিষ্যদ্বাণী করতে চাই।
- $m $ হল লাইনের ঢাল।
- $ x $ হল পাউন্ড—আমাদের ইনপুট মান।
- $b$ হল y-ইন্টারসেপ্ট।
এমএল-এ, আমরা একটি লিনিয়ার রিগ্রেশন মডেলের জন্য সমীকরণটি নিম্নরূপ লিখি:
কোথায়:
- $ y' $ হল পূর্বাভাসিত লেবেল—আউটপুট।
- $b$ হল মডেলের পক্ষপাত । বায়াস একটি লাইনের জন্য বীজগণিতীয় সমীকরণে y-ইন্টারসেপ্টের মতো একই ধারণা। ML-এ, পক্ষপাতকে কখনও কখনও $w_0 $ হিসাবে উল্লেখ করা হয়। বায়াস মডেলের একটি প্যারামিটার এবং প্রশিক্ষণের সময় গণনা করা হয়।
- $w_1 $ হল বৈশিষ্ট্যের ওজন । একটি লাইনের বীজগাণিতিক সমীকরণে ঢাল $m $ হিসাবে ওজন একই ধারণা। ওজন মডেলের একটি প্যারামিটার এবং প্রশিক্ষণের সময় গণনা করা হয়।
- $ x_1 $ হল একটি বৈশিষ্ট্য —ইনপুট।
প্রশিক্ষণের সময়, মডেলটি ওজন এবং পক্ষপাত গণনা করে যা সেরা মডেল তৈরি করে।

চিত্র 3 । একটি লিনিয়ার মডেলের গাণিতিক উপস্থাপনা।
আমাদের উদাহরণে, আমরা যে লাইনটি আঁকেছি তার থেকে আমরা ওজন এবং পক্ষপাত গণনা করব। পক্ষপাত 30 (যেখানে লাইনটি y-অক্ষকে ছেদ করে), এবং ওজন -3.6 (রেখার ঢাল)। মডেলটিকে $y' = 30 + (-3.6)(x_1) $ হিসাবে সংজ্ঞায়িত করা হবে এবং আমরা ভবিষ্যদ্বাণী করতে এটি ব্যবহার করতে পারি। উদাহরণস্বরূপ, এই মডেলটি ব্যবহার করে, একটি 4,000-পাউন্ড গাড়ির প্রতি গ্যালন 15.6 মাইল একটি পূর্বাভাসিত জ্বালানী দক্ষতা থাকবে।

চিত্র 4 । মডেলটি ব্যবহার করে, একটি 4,000-পাউন্ড গাড়ির প্রতি গ্যালন 15.6 মাইল একটি পূর্বাভাসিত জ্বালানী দক্ষতা রয়েছে।
একাধিক বৈশিষ্ট্য সহ মডেল
যদিও এই বিভাগে উদাহরণটি শুধুমাত্র একটি বৈশিষ্ট্য ব্যবহার করে—গাড়ির ভারীতা—একটি আরও পরিশীলিত মডেল একাধিক বৈশিষ্ট্যের উপর নির্ভর করতে পারে, প্রতিটির আলাদা ওজন ($ w_1 $, $ w_2 $, ইত্যাদি)। উদাহরণস্বরূপ, একটি মডেল যা পাঁচটি বৈশিষ্ট্যের উপর নির্ভর করে তা নিম্নরূপ লেখা হবে:
$y' = b + w_1x_1 + w_2x_2 + w_3x_3 + w_4x_4 + w_5x_5 $
উদাহরণস্বরূপ, একটি মডেল যা গ্যাস মাইলেজের পূর্বাভাস দেয় অতিরিক্ত বৈশিষ্ট্যগুলি ব্যবহার করতে পারে যেমন:
- ইঞ্জিন স্থানচ্যুতি
- ত্বরণ
- সিলিন্ডারের সংখ্যা
- অশ্বশক্তি
এই মডেলটি নিম্নরূপ লেখা হবে:

চিত্র 5 । গ্যালন রেটিং প্রতি একটি গাড়ির মাইল ভবিষ্যদ্বাণী করার জন্য পাঁচটি বৈশিষ্ট্য সহ একটি মডেল৷
এই অতিরিক্ত বৈশিষ্ট্যগুলির কিছু গ্রাফ করে, আমরা দেখতে পারি যে তাদের লেবেলের সাথে একটি রৈখিক সম্পর্ক রয়েছে, প্রতি গ্যালন মাইল:

চিত্র 6 । কিউবিক সেন্টিমিটারে একটি গাড়ির স্থানচ্যুতি এবং প্রতি গ্যালন রেটিং এর মাইল। একটি গাড়ির ইঞ্জিন বড় হওয়ার সাথে সাথে এর মাইল প্রতি গ্যালন রেটিং সাধারণত হ্রাস পায়।

চিত্র 7 । একটি গাড়ির ত্বরণ এবং এর মাইল প্রতি গ্যালন রেটিং। যেহেতু একটি গাড়ির ত্বরণ বেশি সময় নেয়, তাই মাইল প্রতি গ্যালন রেটিং সাধারণত বৃদ্ধি পায়।

চিত্র 8 । একটি গাড়ির অশ্বশক্তি এবং এর মাইল প্রতি গ্যালন রেটিং। গাড়ির হর্সপাওয়ার বাড়ার সাথে সাথে মাইল প্রতি গ্যালন রেটিং সাধারণত কমে যায়।
অনুশীলন: আপনার বোঝার পরীক্ষা করুন
এই মডিউলটি রৈখিক রিগ্রেশন ধারণা প্রবর্তন করে।
লিনিয়ার রিগ্রেশন হল একটি পরিসংখ্যানগত কৌশল যা ভেরিয়েবলের মধ্যে সম্পর্ক খুঁজে বের করতে ব্যবহৃত হয়। একটি ML প্রসঙ্গে, লিনিয়ার রিগ্রেশন বৈশিষ্ট্য এবং একটি লেবেলের মধ্যে সম্পর্ক খুঁজে পায়।
উদাহরণস্বরূপ, ধরুন গাড়িটি কতটা ভারী তার উপর ভিত্তি করে আমরা গ্যালন প্রতি মাইলে একটি গাড়ির জ্বালানি দক্ষতার পূর্বাভাস দিতে চাই এবং আমাদের কাছে নিম্নলিখিত ডেটাসেট রয়েছে:
| পাউন্ড ইন 1000 (বৈশিষ্ট্য) | মাইলস প্রতি গ্যালন (লেবেল) |
|---|---|
| 3.5 | 18 |
| 3.69 | 15 |
| 3.44 | 18 |
| 3.43 | 16 |
| ৪.৩৪ | 15 |
| ৪.৪২ | 14 |
| 2.37 | 24 |
যদি আমরা এই পয়েন্টগুলি প্লট করি, আমরা নিম্নলিখিত গ্রাফটি পেতে পারি:

চিত্র 1 । গাড়ির ভারীতা (পাউন্ডে) বনাম মাইল প্রতি গ্যালন রেটিং। একটি গাড়ি যত ভারী হয়, তার মাইল প্রতি গ্যালন রেটিং সাধারণত কমে যায়।
আমরা পয়েন্টগুলির মাধ্যমে একটি সেরা ফিট লাইন অঙ্কন করে আমাদের নিজস্ব মডেল তৈরি করতে পারি:

চিত্র 2 । পূর্ববর্তী চিত্র থেকে ডেটার মাধ্যমে আঁকা একটি সেরা ফিট লাইন।
রৈখিক রিগ্রেশন সমীকরণ
বীজগণিতের ভাষায়, মডেলটিকে $y = mx + b$ হিসাবে সংজ্ঞায়িত করা হবে, যেখানে
- $ y $ হল মাইল প্রতি গ্যালন- যে মান আমরা ভবিষ্যদ্বাণী করতে চাই।
- $m $ হল লাইনের ঢাল।
- $ x $ হল পাউন্ড—আমাদের ইনপুট মান।
- $b$ হল y-ইন্টারসেপ্ট।
এমএল-এ, আমরা একটি লিনিয়ার রিগ্রেশন মডেলের জন্য সমীকরণটি নিম্নরূপ লিখি:
কোথায়:
- $ y' $ হল পূর্বাভাসিত লেবেল—আউটপুট।
- $b$ হল মডেলের পক্ষপাত । বায়াস একটি লাইনের জন্য বীজগণিতীয় সমীকরণে y-ইন্টারসেপ্টের মতো একই ধারণা। ML-এ, পক্ষপাতকে কখনও কখনও $w_0 $ হিসাবে উল্লেখ করা হয়। বায়াস মডেলের একটি প্যারামিটার এবং প্রশিক্ষণের সময় গণনা করা হয়।
- $w_1 $ হল বৈশিষ্ট্যের ওজন । একটি লাইনের বীজগাণিতিক সমীকরণে ঢাল $m $ হিসাবে ওজন একই ধারণা। ওজন মডেলের একটি প্যারামিটার এবং প্রশিক্ষণের সময় গণনা করা হয়।
- $ x_1 $ হল একটি বৈশিষ্ট্য —ইনপুট।
প্রশিক্ষণের সময়, মডেলটি ওজন এবং পক্ষপাত গণনা করে যা সেরা মডেল তৈরি করে।

চিত্র 3 । একটি লিনিয়ার মডেলের গাণিতিক উপস্থাপনা।
আমাদের উদাহরণে, আমরা যে লাইনটি আঁকেছি তার থেকে আমরা ওজন এবং পক্ষপাত গণনা করব। পক্ষপাত 30 (যেখানে লাইনটি y-অক্ষকে ছেদ করে), এবং ওজন -3.6 (রেখার ঢাল)। মডেলটিকে $y' = 30 + (-3.6)(x_1) $ হিসাবে সংজ্ঞায়িত করা হবে এবং আমরা ভবিষ্যদ্বাণী করতে এটি ব্যবহার করতে পারি। উদাহরণস্বরূপ, এই মডেলটি ব্যবহার করে, একটি 4,000-পাউন্ড গাড়ির প্রতি গ্যালন 15.6 মাইল একটি পূর্বাভাসিত জ্বালানী দক্ষতা থাকবে।

চিত্র 4 । মডেলটি ব্যবহার করে, একটি 4,000-পাউন্ড গাড়ির প্রতি গ্যালন 15.6 মাইল একটি পূর্বাভাসিত জ্বালানী দক্ষতা রয়েছে।
একাধিক বৈশিষ্ট্য সহ মডেল
যদিও এই বিভাগে উদাহরণটি শুধুমাত্র একটি বৈশিষ্ট্য ব্যবহার করে—গাড়ির ভারীতা—একটি আরও পরিশীলিত মডেল একাধিক বৈশিষ্ট্যের উপর নির্ভর করতে পারে, প্রতিটির আলাদা ওজন ($ w_1 $, $ w_2 $, ইত্যাদি)। উদাহরণস্বরূপ, একটি মডেল যা পাঁচটি বৈশিষ্ট্যের উপর নির্ভর করে তা নিম্নরূপ লেখা হবে:
$y' = b + w_1x_1 + w_2x_2 + w_3x_3 + w_4x_4 + w_5x_5 $
উদাহরণস্বরূপ, একটি মডেল যা গ্যাস মাইলেজের পূর্বাভাস দেয় অতিরিক্ত বৈশিষ্ট্যগুলি ব্যবহার করতে পারে যেমন:
- ইঞ্জিন স্থানচ্যুতি
- ত্বরণ
- সিলিন্ডারের সংখ্যা
- অশ্বশক্তি
এই মডেলটি নিম্নরূপ লেখা হবে:

চিত্র 5 । গ্যালন রেটিং প্রতি একটি গাড়ির মাইল ভবিষ্যদ্বাণী করার জন্য পাঁচটি বৈশিষ্ট্য সহ একটি মডেল৷
এই অতিরিক্ত বৈশিষ্ট্যগুলির কিছু গ্রাফ করে, আমরা দেখতে পারি যে তাদের লেবেলের সাথে একটি রৈখিক সম্পর্ক রয়েছে, প্রতি গ্যালন মাইল:

চিত্র 6 । কিউবিক সেন্টিমিটারে একটি গাড়ির স্থানচ্যুতি এবং প্রতি গ্যালন রেটিং এর মাইল। একটি গাড়ির ইঞ্জিন বড় হওয়ার সাথে সাথে এর মাইল প্রতি গ্যালন রেটিং সাধারণত হ্রাস পায়।

চিত্র 7 । একটি গাড়ির ত্বরণ এবং এর মাইল প্রতি গ্যালন রেটিং। যেহেতু একটি গাড়ির ত্বরণ বেশি সময় নেয়, তাই মাইল প্রতি গ্যালন রেটিং সাধারণত বৃদ্ধি পায়।

চিত্র 8 । একটি গাড়ির অশ্বশক্তি এবং এর মাইল প্রতি গ্যালন রেটিং। গাড়ির হর্সপাওয়ার বাড়ার সাথে সাথে মাইল প্রতি গ্যালন রেটিং সাধারণত কমে যায়।
অনুশীলন: আপনার বোঝার পরীক্ষা করুন
এই মডিউলটি রৈখিক রিগ্রেশন ধারণা প্রবর্তন করে।
লিনিয়ার রিগ্রেশন হল একটি পরিসংখ্যানগত কৌশল যা ভেরিয়েবলের মধ্যে সম্পর্ক খুঁজে বের করতে ব্যবহৃত হয়। একটি ML প্রসঙ্গে, লিনিয়ার রিগ্রেশন বৈশিষ্ট্য এবং একটি লেবেলের মধ্যে সম্পর্ক খুঁজে পায়।
উদাহরণস্বরূপ, ধরুন গাড়িটি কতটা ভারী তার উপর ভিত্তি করে আমরা গ্যালন প্রতি মাইলে একটি গাড়ির জ্বালানি দক্ষতার পূর্বাভাস দিতে চাই এবং আমাদের কাছে নিম্নলিখিত ডেটাসেট রয়েছে:
| পাউন্ড ইন 1000 (বৈশিষ্ট্য) | মাইলস প্রতি গ্যালন (লেবেল) |
|---|---|
| 3.5 | 18 |
| 3.69 | 15 |
| 3.44 | 18 |
| 3.43 | 16 |
| ৪.৩৪ | 15 |
| ৪.৪২ | 14 |
| 2.37 | 24 |
যদি আমরা এই পয়েন্টগুলি প্লট করি, আমরা নিম্নলিখিত গ্রাফটি পেতে পারি:

চিত্র 1 । গাড়ির ভারীতা (পাউন্ডে) বনাম মাইল প্রতি গ্যালন রেটিং। একটি গাড়ি যত ভারী হয়, তার মাইল প্রতি গ্যালন রেটিং সাধারণত কমে যায়।
আমরা পয়েন্টগুলির মাধ্যমে একটি সেরা ফিট লাইন অঙ্কন করে আমাদের নিজস্ব মডেল তৈরি করতে পারি:

চিত্র 2 । পূর্ববর্তী চিত্র থেকে ডেটার মাধ্যমে আঁকা একটি সেরা ফিট লাইন।
রৈখিক রিগ্রেশন সমীকরণ
বীজগণিতের ভাষায়, মডেলটিকে $y = mx + b$ হিসাবে সংজ্ঞায়িত করা হবে, যেখানে
- $ y $ হল মাইল প্রতি গ্যালন- যে মান আমরা ভবিষ্যদ্বাণী করতে চাই।
- $m $ হল লাইনের ঢাল।
- $ x $ হল পাউন্ড—আমাদের ইনপুট মান।
- $b$ হল y-ইন্টারসেপ্ট।
এমএল-এ, আমরা একটি লিনিয়ার রিগ্রেশন মডেলের জন্য সমীকরণটি নিম্নরূপ লিখি:
কোথায়:
- $ y' $ হল পূর্বাভাসিত লেবেল—আউটপুট।
- $b$ হল মডেলের পক্ষপাত । বায়াস একটি লাইনের জন্য বীজগণিতীয় সমীকরণে y-ইন্টারসেপ্টের মতো একই ধারণা। ML-এ, পক্ষপাতকে কখনও কখনও $w_0 $ হিসাবে উল্লেখ করা হয়। বায়াস মডেলের একটি প্যারামিটার এবং প্রশিক্ষণের সময় গণনা করা হয়।
- $w_1 $ হল বৈশিষ্ট্যের ওজন । একটি লাইনের বীজগাণিতিক সমীকরণে ঢাল $m $ হিসাবে ওজন একই ধারণা। ওজন মডেলের একটি প্যারামিটার এবং প্রশিক্ষণের সময় গণনা করা হয়।
- $ x_1 $ হল একটি বৈশিষ্ট্য —ইনপুট।
প্রশিক্ষণের সময়, মডেলটি ওজন এবং পক্ষপাত গণনা করে যা সেরা মডেল তৈরি করে।

চিত্র 3 । একটি লিনিয়ার মডেলের গাণিতিক উপস্থাপনা।
আমাদের উদাহরণে, আমরা যে লাইনটি আঁকেছি তার থেকে আমরা ওজন এবং পক্ষপাত গণনা করব। পক্ষপাত 30 (যেখানে লাইনটি y-অক্ষকে ছেদ করে), এবং ওজন -3.6 (রেখার ঢাল)। মডেলটিকে $y' = 30 + (-3.6)(x_1) $ হিসাবে সংজ্ঞায়িত করা হবে এবং আমরা ভবিষ্যদ্বাণী করতে এটি ব্যবহার করতে পারি। উদাহরণস্বরূপ, এই মডেলটি ব্যবহার করে, একটি 4,000-পাউন্ড গাড়ির প্রতি গ্যালন 15.6 মাইল একটি পূর্বাভাসিত জ্বালানী দক্ষতা থাকবে।

চিত্র 4 । মডেলটি ব্যবহার করে, একটি 4,000-পাউন্ড গাড়ির প্রতি গ্যালন 15.6 মাইল একটি পূর্বাভাসিত জ্বালানী দক্ষতা রয়েছে।
একাধিক বৈশিষ্ট্য সহ মডেল
যদিও এই বিভাগে উদাহরণটি শুধুমাত্র একটি বৈশিষ্ট্য ব্যবহার করে—গাড়ির ভারীতা—একটি আরও পরিশীলিত মডেল একাধিক বৈশিষ্ট্যের উপর নির্ভর করতে পারে, প্রতিটির আলাদা ওজন ($ w_1 $, $ w_2 $, ইত্যাদি)। উদাহরণস্বরূপ, একটি মডেল যা পাঁচটি বৈশিষ্ট্যের উপর নির্ভর করে তা নিম্নরূপ লেখা হবে:
$y' = b + w_1x_1 + w_2x_2 + w_3x_3 + w_4x_4 + w_5x_5 $
উদাহরণস্বরূপ, একটি মডেল যা গ্যাস মাইলেজের পূর্বাভাস দেয় অতিরিক্ত বৈশিষ্ট্যগুলি ব্যবহার করতে পারে যেমন:
- ইঞ্জিন স্থানচ্যুতি
- ত্বরণ
- সিলিন্ডারের সংখ্যা
- অশ্বশক্তি
এই মডেলটি নিম্নরূপ লেখা হবে:

চিত্র 5 । গ্যালন রেটিং প্রতি একটি গাড়ির মাইল ভবিষ্যদ্বাণী করার জন্য পাঁচটি বৈশিষ্ট্য সহ একটি মডেল৷
এই অতিরিক্ত বৈশিষ্ট্যগুলির কিছু গ্রাফ করে, আমরা দেখতে পারি যে তাদের লেবেলের সাথে একটি রৈখিক সম্পর্ক রয়েছে, প্রতি গ্যালন মাইল:

চিত্র 6 । কিউবিক সেন্টিমিটারে একটি গাড়ির স্থানচ্যুতি এবং প্রতি গ্যালন রেটিং এর মাইল। একটি গাড়ির ইঞ্জিন বড় হওয়ার সাথে সাথে এর মাইল প্রতি গ্যালন রেটিং সাধারণত হ্রাস পায়।

চিত্র 7 । একটি গাড়ির ত্বরণ এবং এর মাইল প্রতি গ্যালন রেটিং। যেহেতু একটি গাড়ির ত্বরণ বেশি সময় নেয়, তাই মাইল প্রতি গ্যালন রেটিং সাধারণত বৃদ্ধি পায়।

চিত্র 8 । একটি গাড়ির অশ্বশক্তি এবং এর মাইল প্রতি গ্যালন রেটিং। গাড়ির হর্সপাওয়ার বাড়ার সাথে সাথে মাইল প্রতি গ্যালন রেটিং সাধারণত কমে যায়।
