W tym module przedstawiamy pojęcia związane z regresją liniową.
Regresja liniowa to: metoda statystyczna używana do wykrywania zależności między zmiennymi. W ML w kontekście, regresja liniowa znajduje zależność między funkcje oraz label.
Załóżmy np., że chcemy przewidzieć zużycie paliwa przez samochód w milach na galonów w zależności od wagi samochodu, mamy następujący zbiór danych:
| Funty w tysiącach (funkcja) | Mile na galon (etykieta) |
|---|---|
| 3,5 | 18 |
| 3,69 | 15 |
| 3,44 | 18 |
| 3,43 | 16 |
| 4,34 | 15 |
| 4,42 | 14 |
| 2,37 | 24 |
Gdybyśmy chcieli nakreślić te punkty, uzyskalibyśmy następujący wykres:
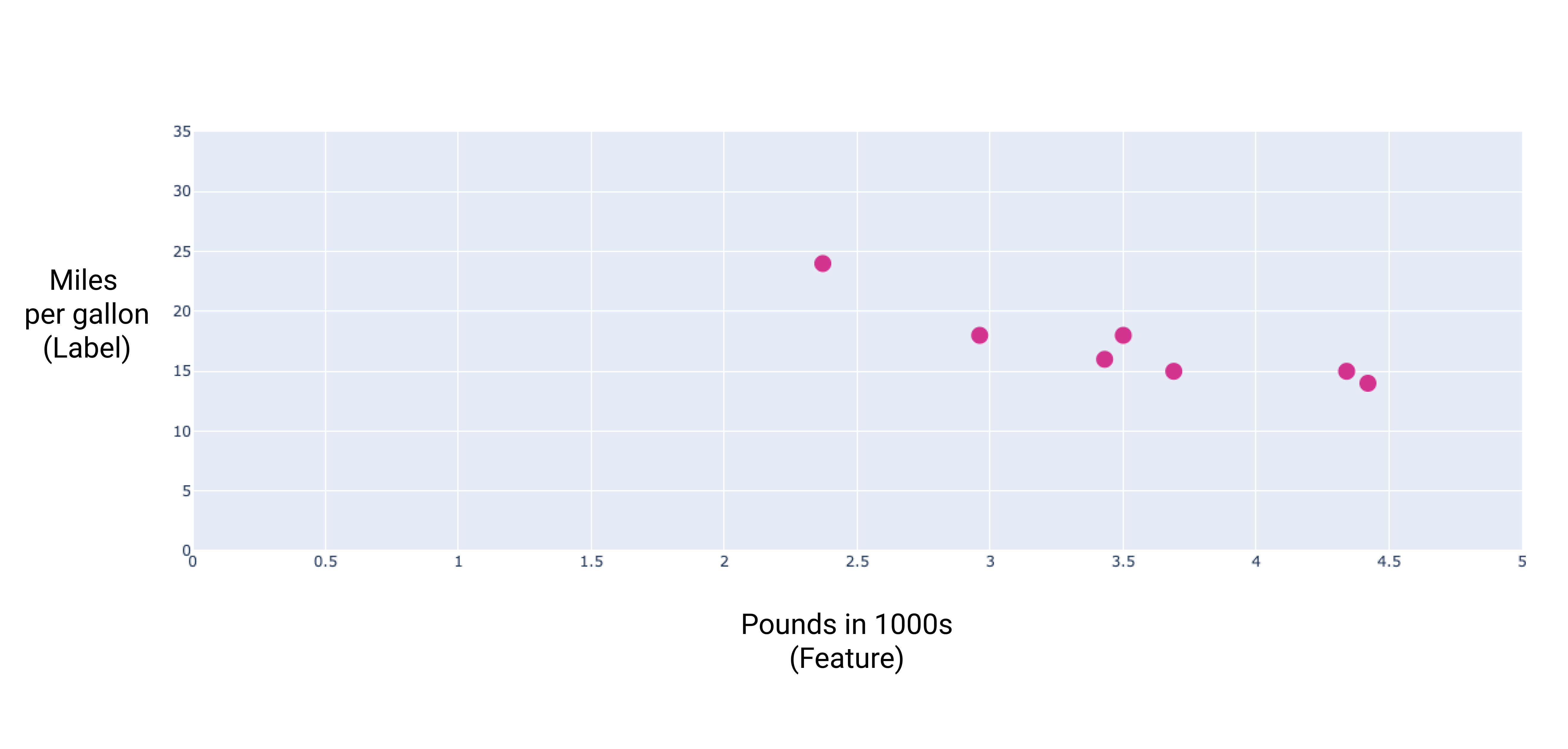
Rysunek 1. Ciężar samochodu (w funtach) w porównaniu z oceną mil na galon. Jako samochód staje się cięższy, jego wartość mil na galon zazwyczaj spada.
Mogliśmy utworzyć własny model, rysując linię najlepiej pasującą do punktów:
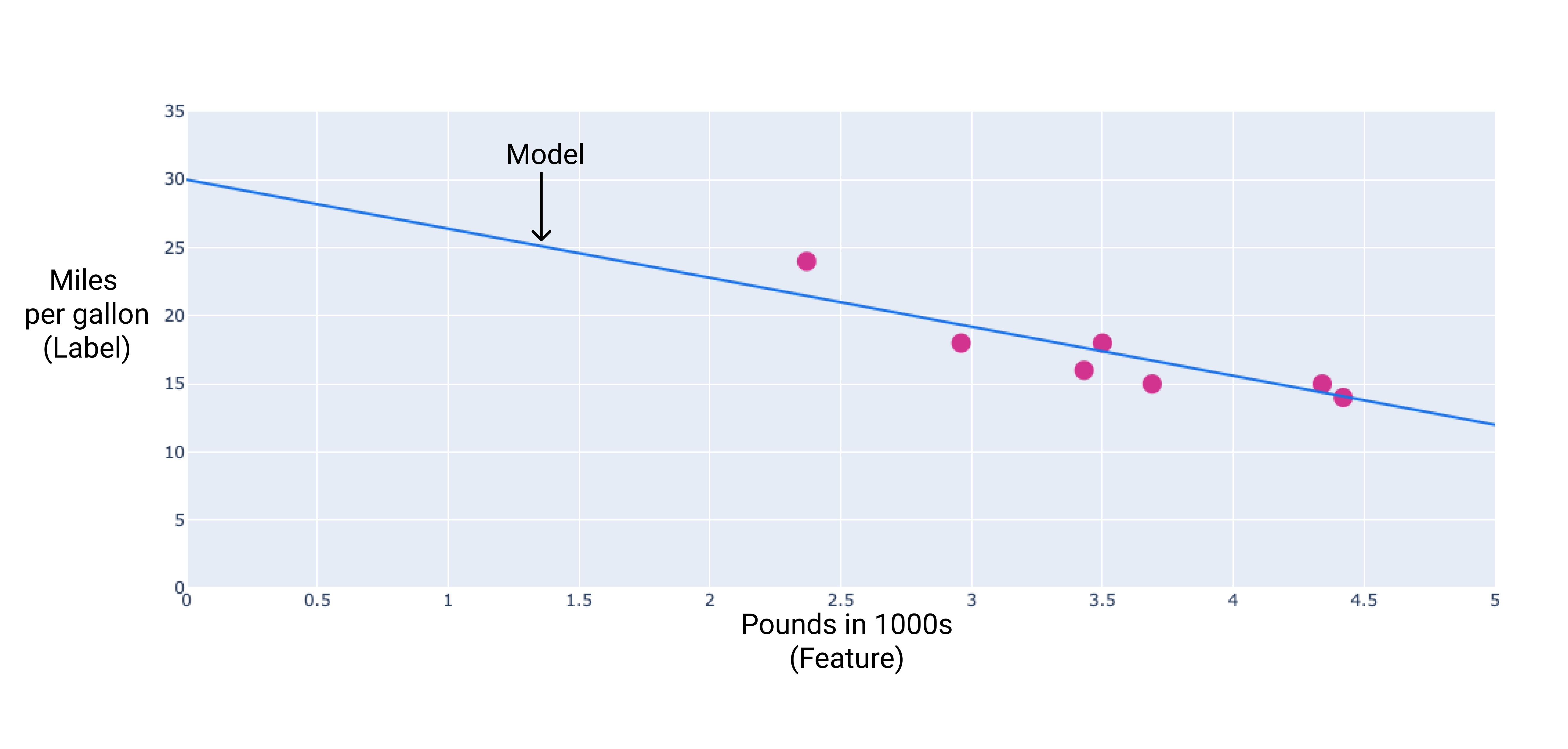
Rysunek 2. Najdokładniejsza linia utworzona na podstawie danych z poprzedniego rysunku.
Równanie regresji liniowej
W warunkach algebraicznych model zostałby zdefiniowany jako $ y = mx + b $, gdzie:
- $ y $ to mile na galon—czyli wartość, którą chcemy prognozować.
- $ m $ to nachylenie linii.
- $ x $ to funty – nasza wartość wejściowa.
- Argument $ b $ to punkt przecięcia z osią y.
W ML zapisujemy równanie modelu regresji liniowej w ten sposób:
gdzie:
- $ y' $ to prognozowana etykieta – dane wyjściowe.
- $ b $ to uprzedzenia modelu. Odchylenie to ta sama koncepcja, co punkt przecięcia z osią y w funkcji algebraicznych równanie prostej. W ML uprzedzenie jest czasami określane mianem $ w_0 USD. Uprzedzenia jest parametrem modelu, jest obliczany podczas trenowania.
- $ w_1 $ to waga funkcji. Waga jest taka sama jak nachylenie $ m $ w algebraicznym znaczeniu równanie prostej. Waga jest parameter modelu i jest obliczonych podczas trenowania.
- $ x_1 $ to funkcja – dane wejściowe.
Podczas trenowania model oblicza wagę i odchylenie, które dają najlepsze model atrybucji.
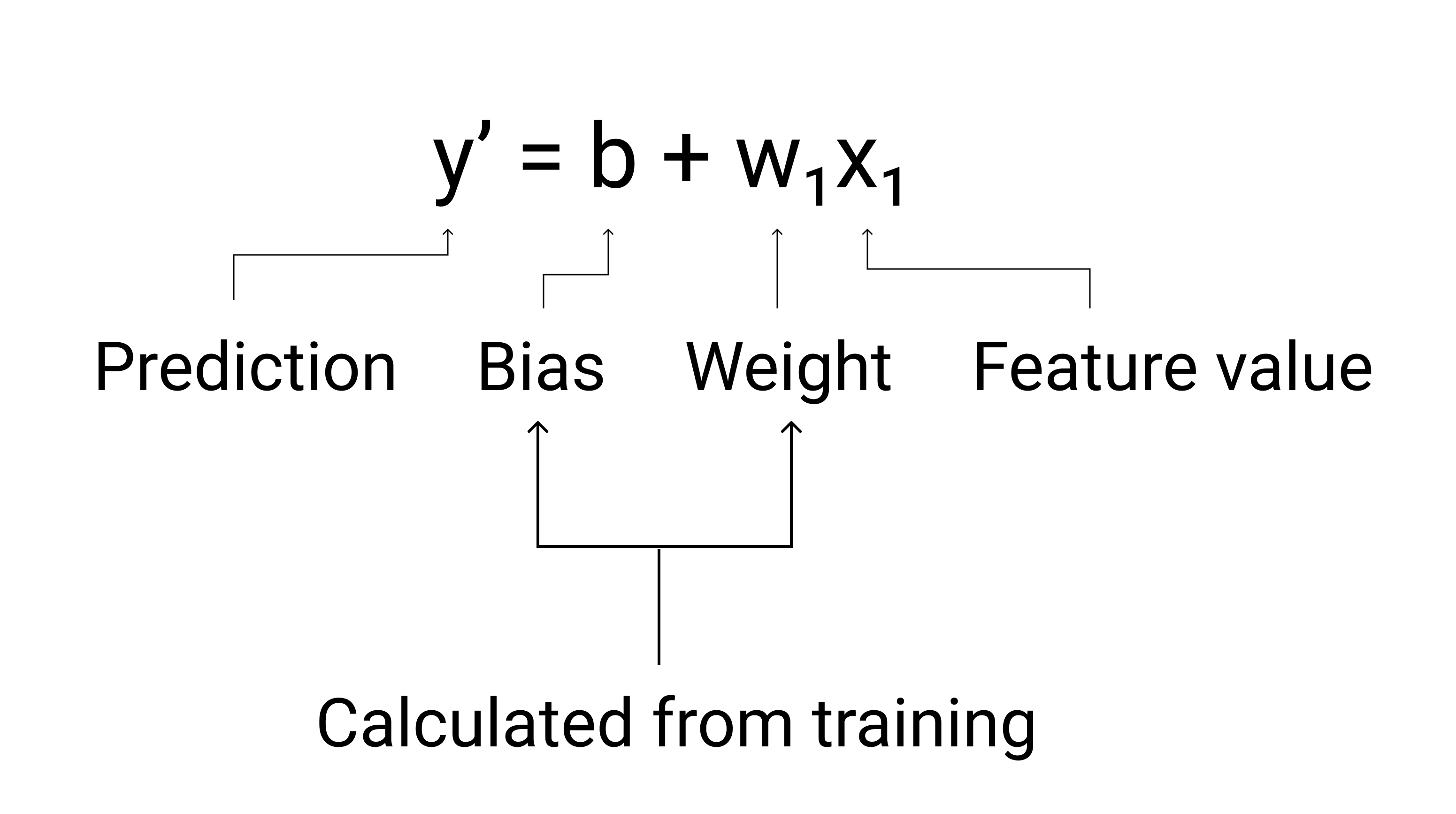
Rysunek 3. Matematyczna reprezentacja modelu liniowego.
W naszym przykładzie obliczymy wagę i odchylenie na podstawie narysowanej linii. odchylenie wynosi 30 (gdzie linia przecina oś Y), a waga wynosi -3,6 ( nachylenie prostej). Model zostałby zdefiniowany jako $ y' = 30 + (-3, 6)(x_1) USD oraz których możemy użyć do prognozowania. Na przykład w tym modelu Samochód o wadze 1200 kg miałby przewidywane zużycie paliwa na poziomie 25,6 mili galonów.
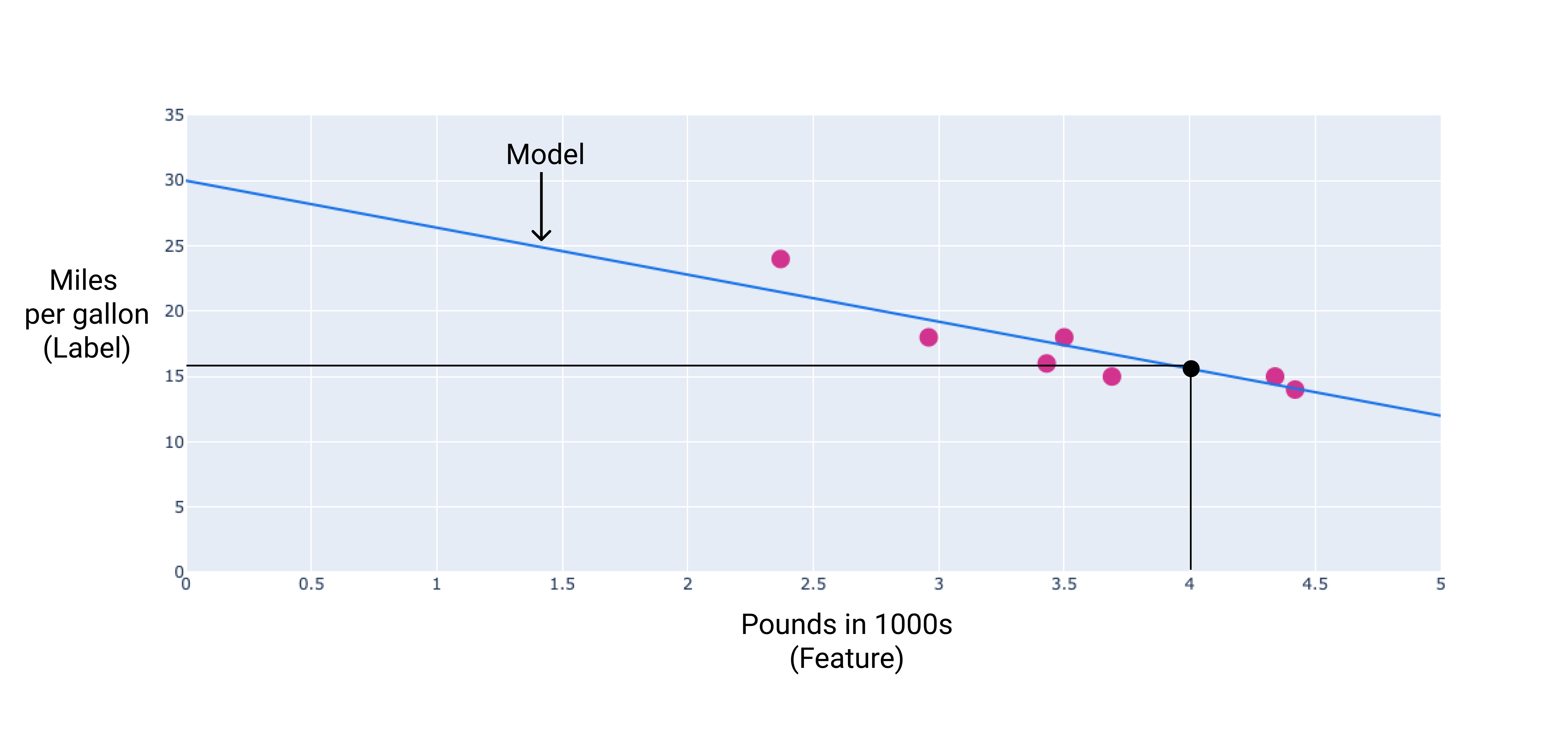
Rysunek 4. Za pomocą tego modelu samochód ważący 1200 kg według prognozy spalanie 15,5 km na litr.
Modele z wieloma funkcjami
W przykładzie w tej sekcji wykorzystano tylko jedną cechę – samochodu – bardziej zaawansowany model może bazować na wielu funkcjach, które mają oddzielną wagę ($ w_1 $, $ w_2 $ itd.). Na przykład model która opiera się na 5 funkcjach, brzmiała tak:
$ y' = b + W_1x_1 + W_2x_2 + W_3x_3 + W_4x_4 + szer._5x_5 zł
Na przykład model prognozujący zużycie paliwa może dodatkowo korzystać z funkcji na przykład:
- Pojemność silnika
- Przyspieszenie
- Liczba cylind
- Koń parowy
Ten model zostałby zapisany w taki sposób:
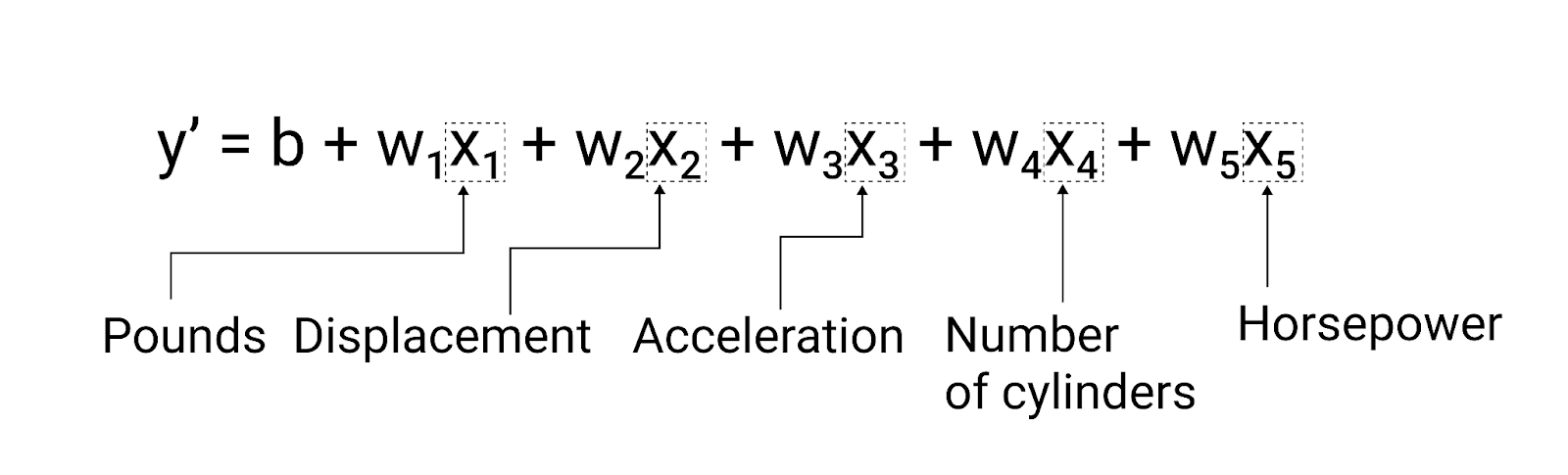
Rysunek 5. Model z 5 funkcjami do przewidywania mil na galon samochodu ocenę.
Na wykresie niektórych dodatkowych funkcji można zobaczyć, że mają one również stosunek liniowy do etykiety, mile na galon:
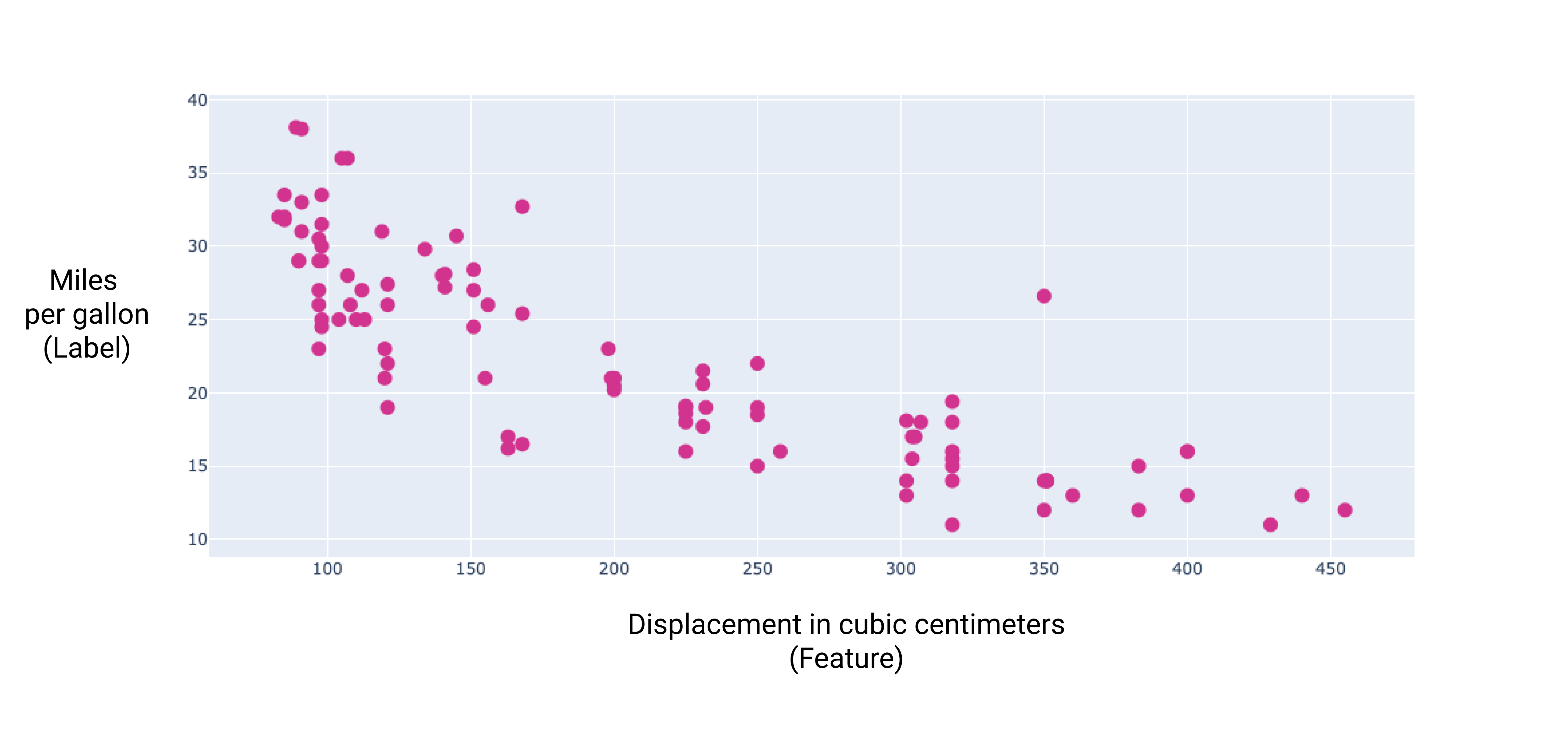
Rysunek 6. Przemieszczenie samochodu w centymetrach sześciennych i jego milach na galon ocenę. Gdy silnik samochodu zwiększa się, jego iloraz mil na galon maleje.
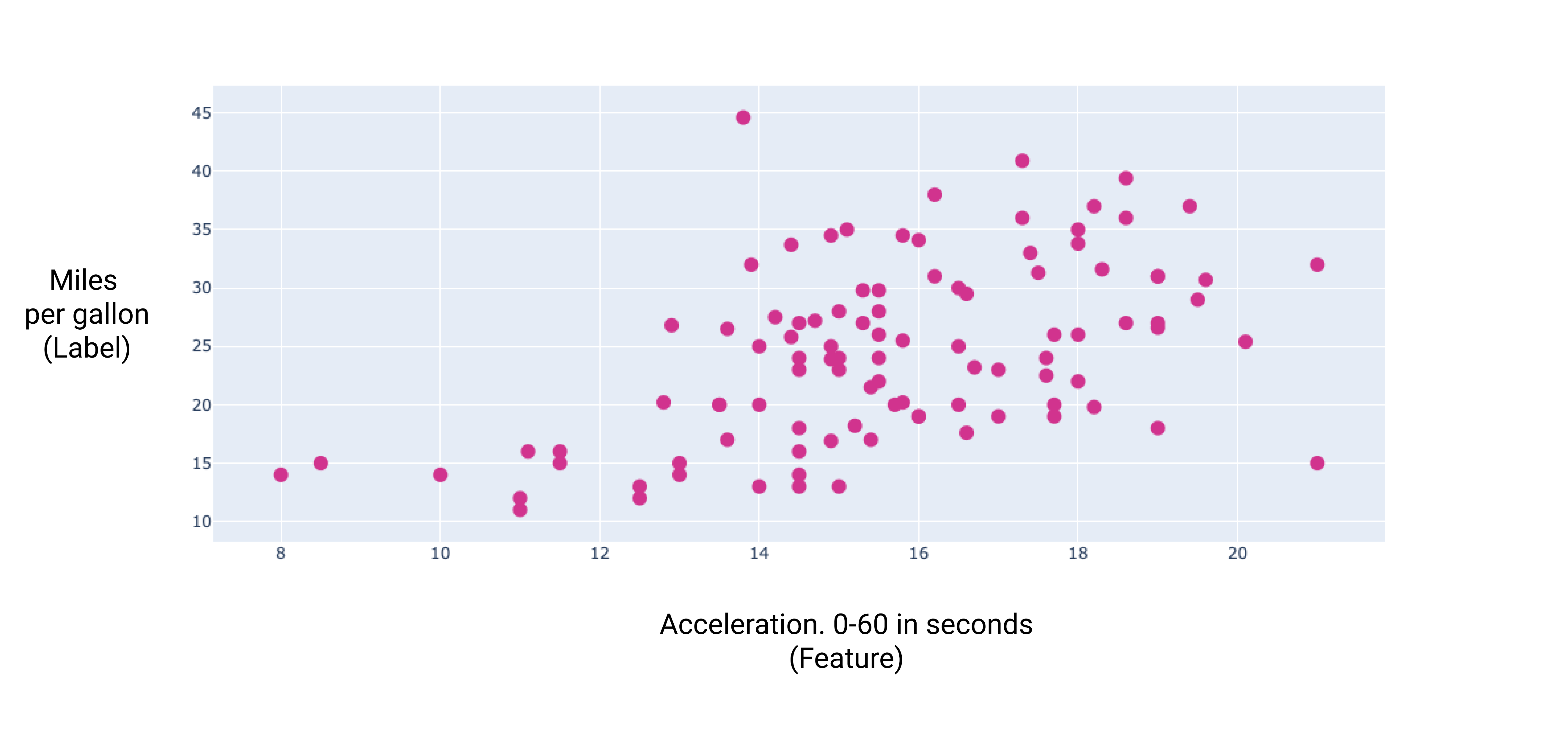
Rysunek 7. Przyspieszenie samochodu i jego mila na galon. Jako samochód przyspieszenie trwa dłużej, więc zazwyczaj zwiększa się liczba mil na galon.
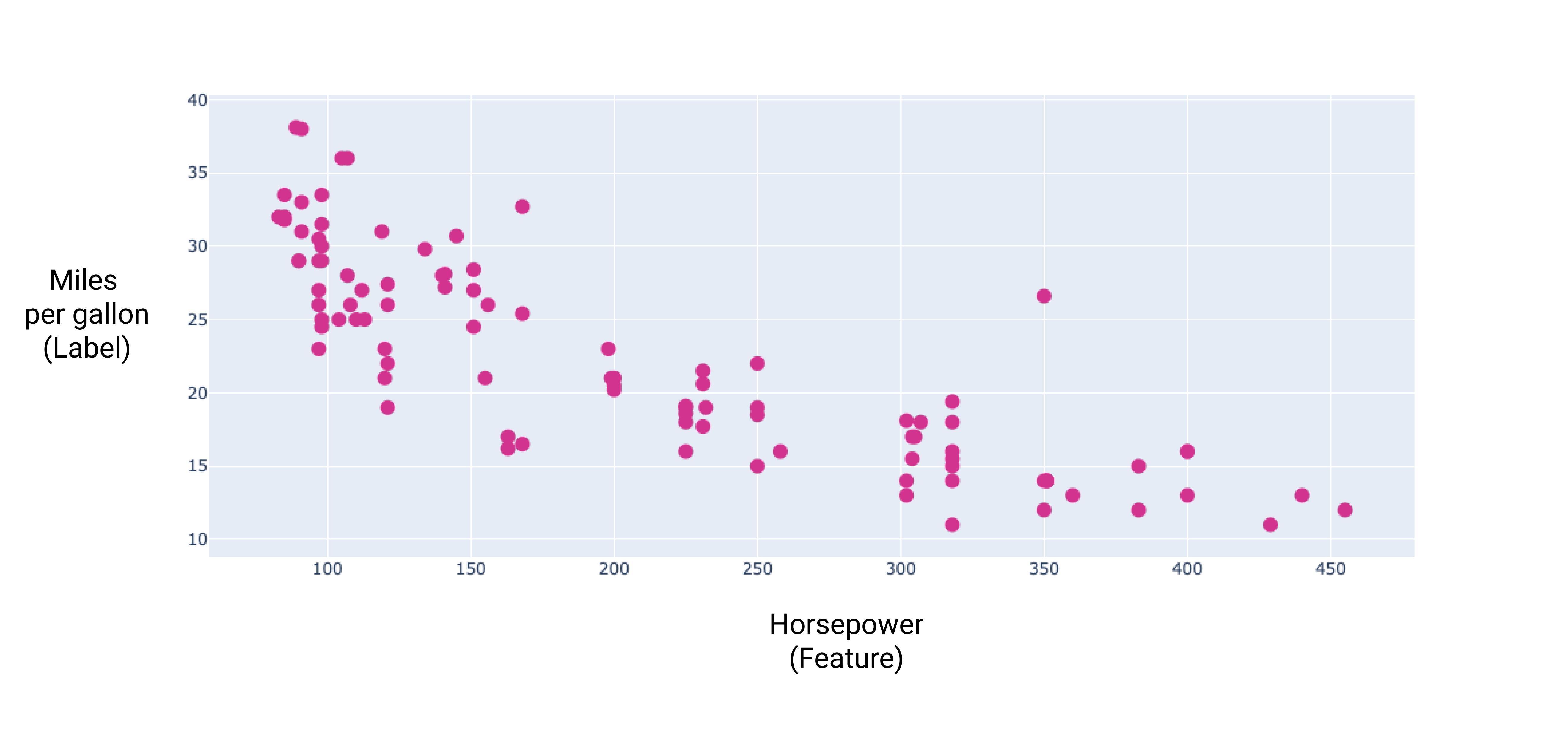
Rysunek 8. Moc samochodu i liczba mil na galon. Jako samochód koni mechanicznych, spada liczba mil na galon.
