מוקדם יותר, נתקלת בבעיה סיווג בינארי שיכול לבחור באחת מתוך שתיים אפשרויות אפשריות, למשל:
- אימייל מסוים הוא ספאם או לא ספאם.
- גידול נתון הוא ממאיר או שפיר.
בחלק הזה נסביר על סיווג לכמה כיתות של מודלים, שאפשר לבחור מתוך מספר אפשרויות. לדוגמה:
- האם הכלב הזה הוא ביגל, כלב באסט או כלב דם?
- האם הפרח הזה הוא אירוס סיבירי, אירוס ההולנדי, אירוס הדגל הכחול, או אירוס לזקן?
- האם המטוס הזה הוא מדגם Boeing 747, Airbus 320, בואינג 777 או Embraer 190?
- האם זו תמונה של תפוח, דוב, ממתק, כלב או ביצה?
יש כמה בעיות בעולם האמיתי שכוללות מיליוניות, של סיווגים נפרדים. לדוגמה, נבחן את הסיווג של כמה כיתות שיכול לזהות תמונה כמעט של כל דבר.
בקטע הזה מפורטות שתי הווריאציות העיקריות של סיווג על ידי מספר כיתות:
- אחד לעומת הכול
- one-vs.-one, שידוע בדרך כלל בשם softmax
אחד לעומת כולם
One-vs.-all מאפשר להשתמש בסיווג בינארי לסדרה של חיזויים מסוג 'כן' או 'לא' בכמה תוויות אפשריות.
בהינתן בעיית סיווג של N פתרונות אפשריים, אחד נגד כולם הפתרון מורכב מ-N מסווגים בינאריים נפרדים - ערך בינארי אחד של כל תוצאה אפשרית. במהלך האימון, המודל מפעיל באמצעות רצף של מסַווגים בינאריים, שמאמנים כל אחד מהם לענות על לשאלת הסיווג.
לדוגמה, בהינתן תמונה של חתיכת פרי, עשויים להיות מאמנים מזהים שונים, וכל אחד מהם עונה על השאלה 'כן/לא' אחרת שאלה:
- האם התמונה הזו היא תפוח?
- האם התמונה הזו היא כתפוז?
- האם התמונה הזו היא בננה?
- האם התמונה הזו היא ענבים?
התמונה הבאה ממחישה איך זה עובד בפועל.
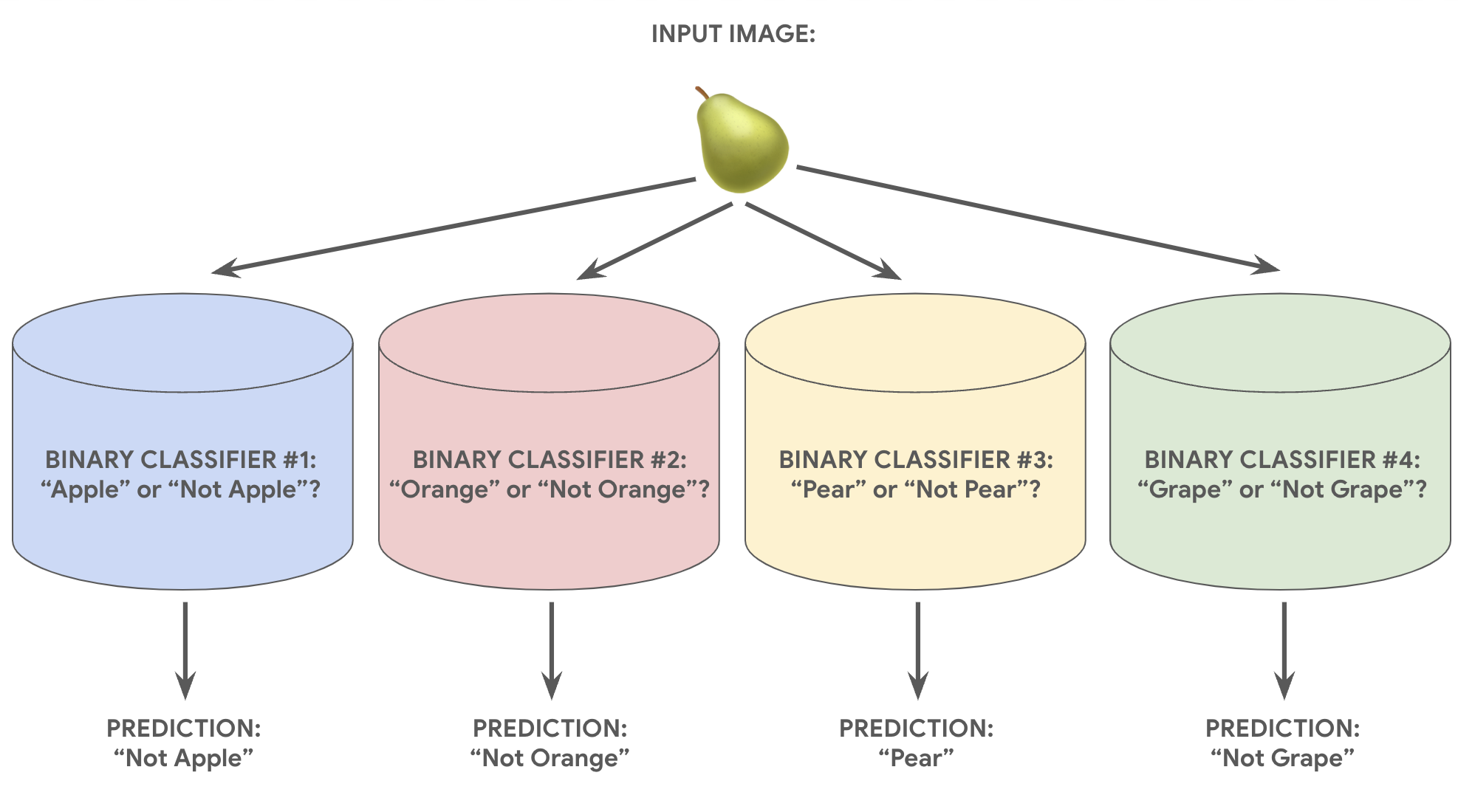
הגישה הזו סבירה למדי כאשר המספר הכולל של הכיתות קטן, אך הופך לבלתי יעיל יותר ויותר ככל שמספר הכיתות עולה.
אנחנו יכולים ליצור מודל יעילות יותר בהרבה, אחד מול כולם עם רשת נוירונים עמוקה שבה כל צומת פלט מייצג בכיתה. התמונה הבאה ממחישה את הגישה הזו.
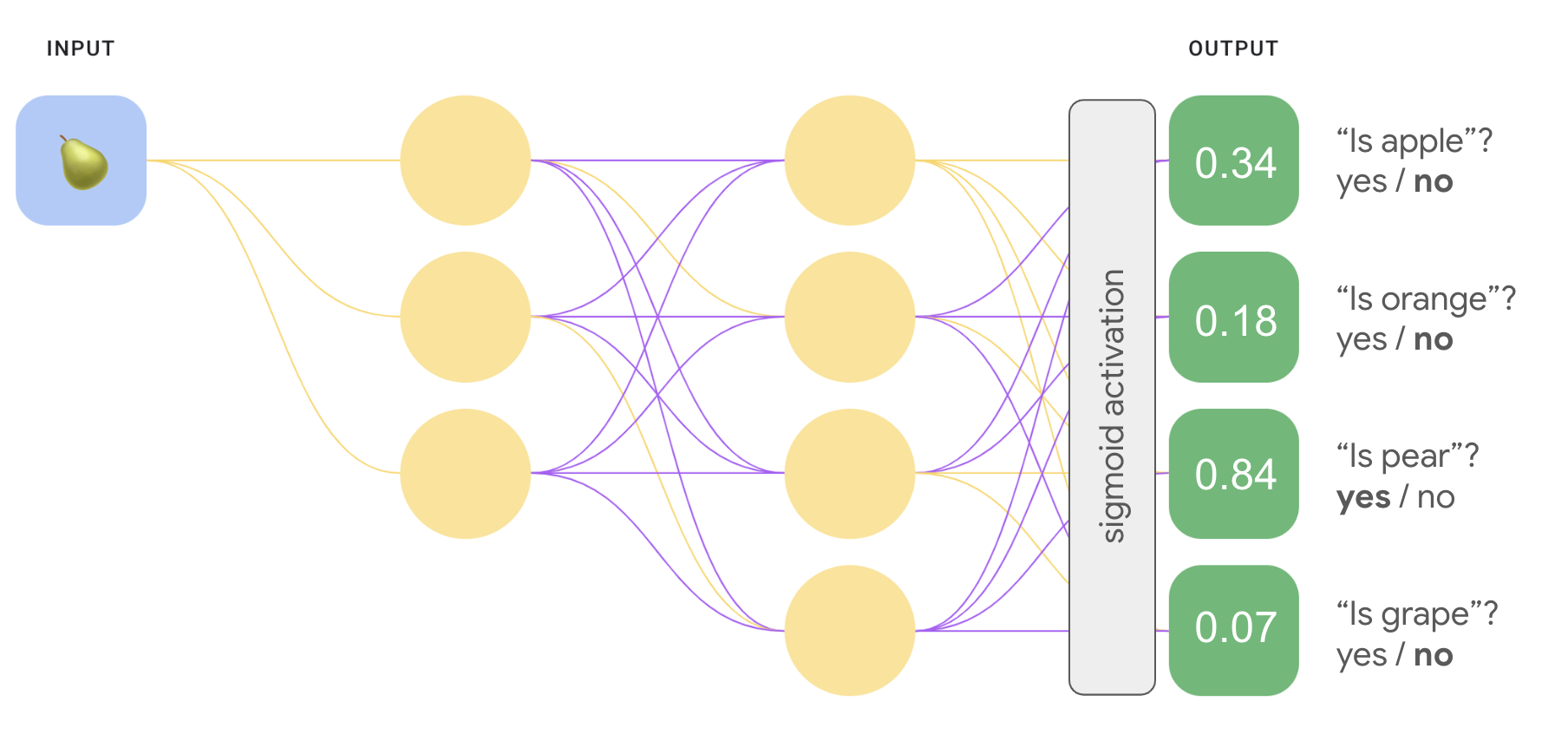
אחת לעומת אחת (softmax)
אולי הבחנתם שערכי ההסתברות בשכבת הפלט של איור 8 לא מסתכמים ב-1.0 (או 100%). (למעשה, הם מסתכמים ב-1.43.) במשחק אחד נגד כולם ההסתברות של כל קבוצה בינארית של תוצאות נקבעת בנפרד מכל הקבוצות האחרות. כלומר, אנחנו קובעים מתוך "apple" לעומת 'not apple' בלי להביא בחשבון את הסבירות אפשרויות פירות: "כתום", "אגס" או "ענבים".
אבל מה אם רוצים לחזות את ההסתברויות של כל פרי יחסית זה לזה? במקרה כזה, במקום לחזות את המילה "apple" לעומת 'לא' אנחנו רוצים לחזות את תפוח, לעומת 'כתום' לעומת 'אגס' לעומת 'ענבים'. הסוג הזה של סיווג בכמה כיתות נקרא סיווג של אחד לעומת אחד.
אפשר ליצור סיווג של אחד מול אחד באמצעות אותו סוג של נוירונים ארכיטקטורת רשת שמשמשת לסיווג של אחד מול כולם, עם שינוי מרכזי אחד. אנחנו צריכים להחיל טרנספורמציה אחרת על שכבת הפלט.
לאחד לעומת כולם, החלנו את פונקציית ההפעלה sigmoid על כל פלט בנפרד, ולכן ערך הפלט היה בין 0 ל-1 אבל לא הבטחה לכך שהערכים האלו יסכמו ל-1 בדיוק.
בשביל אחד לעומת אחד, אפשר להחיל במקום זאת פונקציה שנקראת softmax מקצה הסתברויות עשרוניות לכל מחלקה בבעיה רב-סיווגית, כך כל ההסתברויות מסתכמות ב-1.0. האילוץ הנוסף הזה שמאפשר אימון מתכנס מהר יותר מכפי שהוא היה.
בתמונה הבאה אנחנו מיישמים מחדש את הסיווג שלנו ברמה אחת מול כולם כמשימה של אחד נגד אחד. שימו לב שכדי לבצע הפעלה של softmax, צריך השכבה שלפני שכבת הפלט (שנקראת שכבת ה-softmax) אותו מספר צמתים כמו בשכבת הפלט.

אפשרויות ל-Softmax
כדאי להשתמש בווריאציות הבאות של softmax:
Full softmax הוא ה-softmax שדיברנו עליו; כלומר, הפונקציה softmax מחשבת הסתברות לכל מחלקה אפשרית.
דגימת מועמדים פירושה שהמערכת של softmax מחשבת הסתברות לגבי כל התוויות החיוביות אבל רק עבור מדגם אקראי של תוויות שליליות. לדוגמה, אם אנחנו רוצים לקבוע בין שתמונת קלט היא ביגל או כלב דם, אנחנו לא צריכים מספק הסתברויות לכל דוגמה שאינה של כלבים.
תוסף softmax מלא הוא די זול כשמספר הכיתות קטן אבל המחיר הופך ליקר מדי כשמספר הכיתות עולה. דגימת מועמדים יכולה לשפר את היעילות בבעיות של מספר הכיתות.
תווית אחת לעומת תוויות רבות
Softmax מניח שכל דוגמה היא חברה במחלקה אחת בדיוק. עם זאת, חלק מהדוגמאות יכולות להיכלל במספר כיתות בו-זמנית. לדוגמה:
- אין להשתמש ב-softmax.
- עליכם להסתמך על רגרסיות לוגיסטיות מרובות.
לדוגמה, המודל אחד לעומת אחד באיור 9 שלמעלה מניח שכל קלט התמונה תציג בדיוק סוג אחד של פרי: תפוח, תפוז, אגס או ענבים. עם זאת, אם תמונת קלט עשויה להכיל כמה סוגים של פירות - קערה של תפוחים ותפוזים – תצטרכו להשתמש בהרבה לוגיסטי רגרסיות במקום זאת.
