Нейронні мережі: багатокласова класифікація

Раніше ви стикалися з моделями двійкової класифікації, які могли вибирати один із двох можливих варіантів, наприклад визначати:

• є певний електронний лист спамом чи ні;
• злоякісна певна пухлина чи доброякісна.

У цьому розділі розглядаються моделі багатокласової класифікації, які можуть вибирати з багатьох варіантів. Наприклад, вони можуть дати відповіді на запитання, наведені нижче.

• Порода цього пса – бігль, басет-гаунд чи бладгаунд?
• Ця квітка – "півник сибірський", "півник голландський", "півник різнобарвний" чи "півник німецький"?
• Цей літак – Boeing 747, Airbus 320, Boeing 777 чи Embraer 190?
• Це зображення яблука, ведмедя, цукерки, собаки чи яйця?

Деякі багатокласові задачі, для яких використовують моделі на практиці, передбачають вибір із мільйонів окремих класів. Наприклад, розгляньмо модель багатокласової класифікації, яка може ідентифікувати зображення майже будь-чого.

У цьому розділі докладно описано два основних методи багатокласової класифікації:

• "один проти всіх" (one-vs.-all);
• "один проти одного" (one-vs.-one) (зазвичай називається функцією м’якого максимуму, або softmax).

"Один проти всіх"

Метод один проти всіх дає змогу використовувати двійкову класифікацію, щоб робити ряд прогнозів "так" або "ні" для кількох можливих міток.

Якщо задача класифікації має N можливих варіантів, у рішенні "один проти всіх" буде N окремих двійкових класифікаторів – по одному для кожного можливого результату. Для реалізації цього рішення тренується послідовність двійкових класифікаторів: кожен із них навчається відповідати на окреме запитання класифікації.

Наприклад, маючи зображення шматочка фрукта, можна навчити чотири різні моделі для розпізнавання, кожна з яких відповідатиме на інше запитання, що вимагає відповіді "так" чи "ні". Приклади запитань наведено нижче.

1. Це зображення яблука?
2. Це зображення апельсина?
3. Це зображення банана?
4. Це зображення винограду?

На зображенні нижче показано, як це працює на практиці.

Рисунок 7. Зображення груші, яке передається як вхідні дані в чотири різні двійкові класифікатори. Перша, друга й четверта моделі (які визначають, є зображення, відповідно, яблуком, апельсином або виноградом чи ні) прогнозують негативний клас. Третя модель (яка визначає, є зображення грушею чи ні) прогнозує позитивний клас.

Докладну інформацію про те, як двійкові класифікатори роблять прогнози (як установити поріг класифікації для перетворення числових результатів роботи моделі в позитивну чи негативну мітку), наведено в модулі Класифікація.

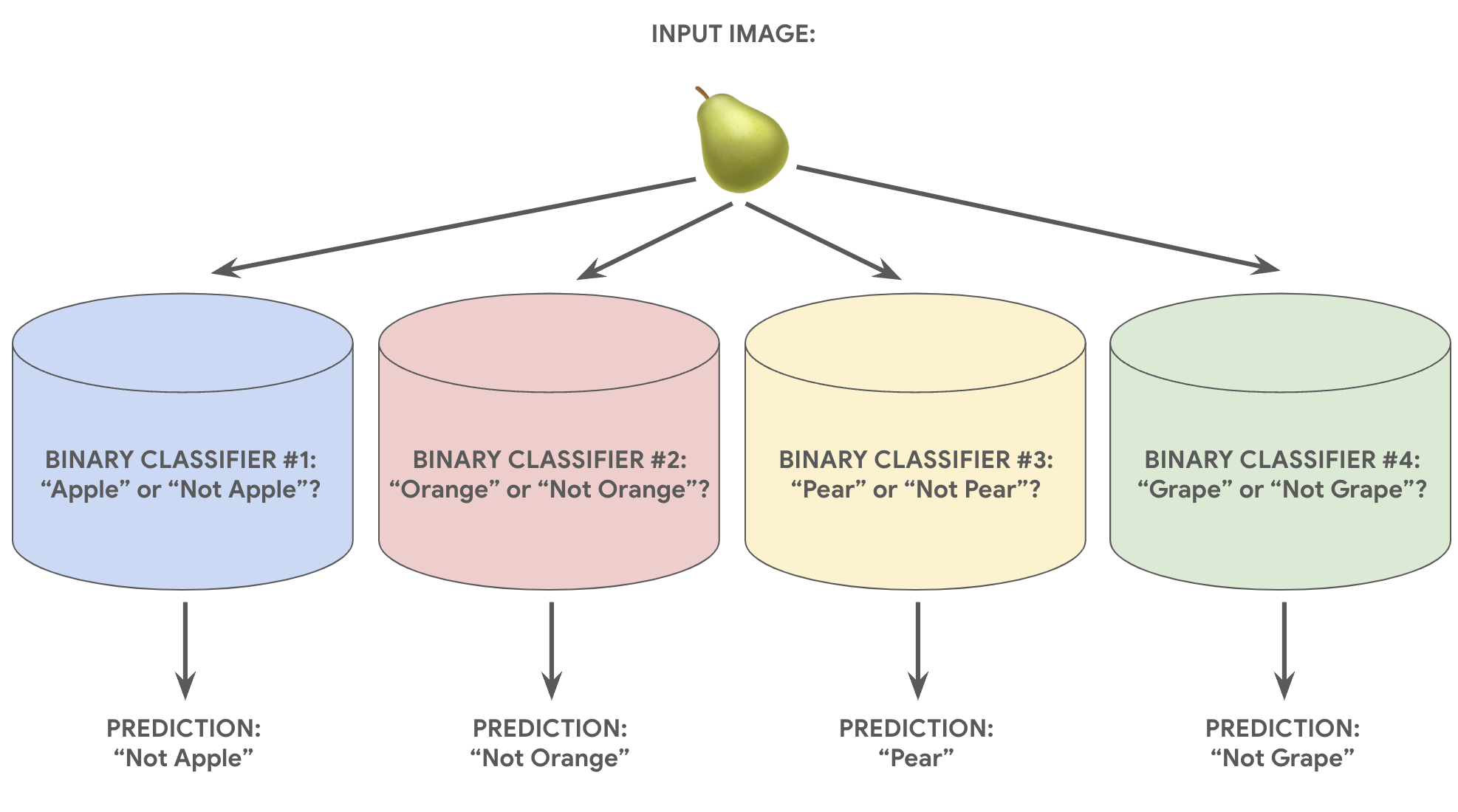
Цей підхід розумний, якщо загальна кількість класів невелика, але що більше їх стає, то менш ефективним він є.

Можна створити значно ефективнішу модель "один проти всіх" із глибинною нейронною мережею, у якій кожен вихідний вузол представляє інший клас. Цей підхід показано на зображенні нижче.

Рисунок 8. Ті самі завдання класифікації "один проти всіх", виконані за допомогою моделі нейронної мережі. Сигмоїдна функція активації застосовується до вихідного шару, і кожне вихідне значення – це ймовірність того, що вхідне зображення є вказаним фруктом. Ця модель визначила, що ймовірність того, що зображення є грушею, становить 84%, а виноградом – 7%.

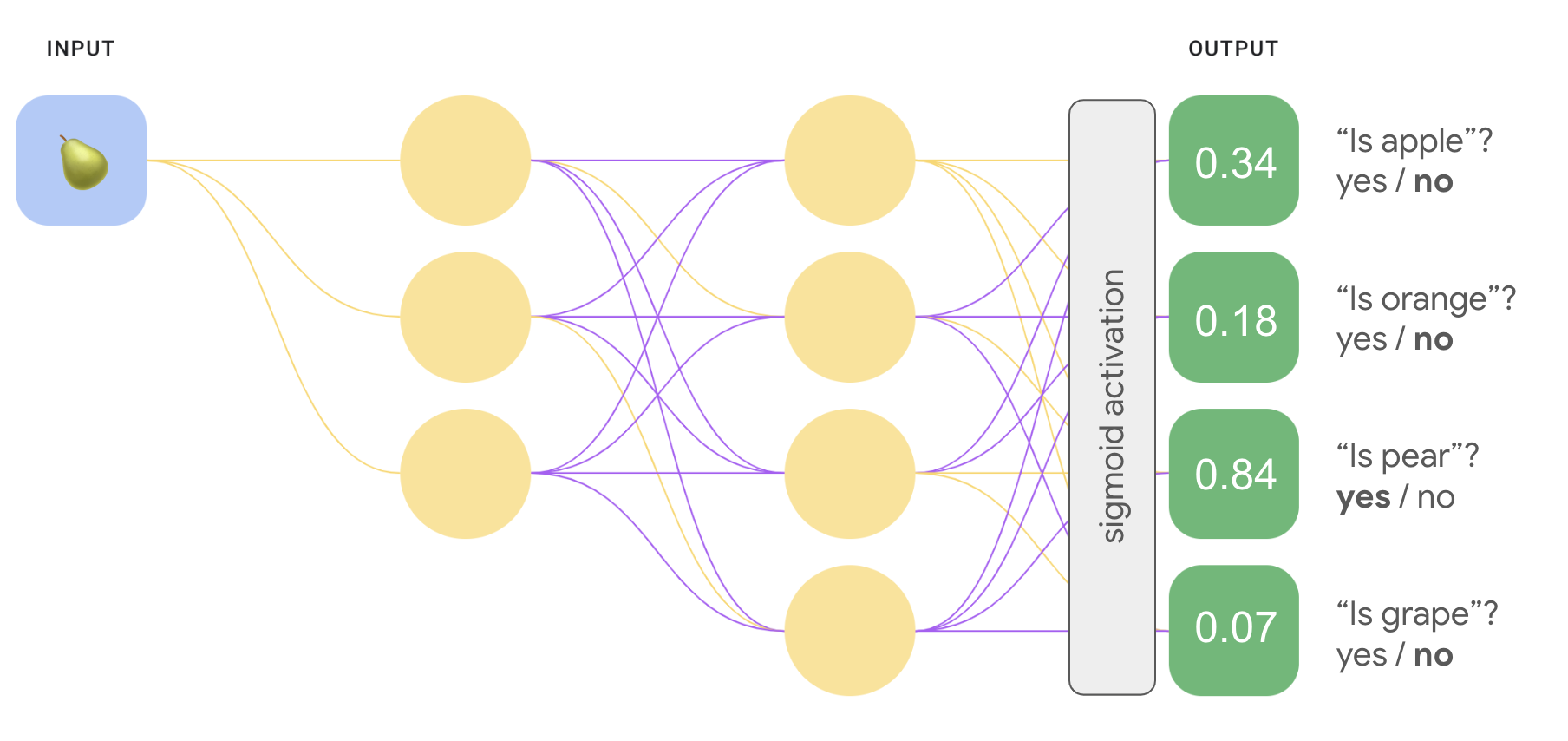
"Один проти одного" (softmax)

Можливо, ви помітили, що значення ймовірності вихідного шару на рисунку 8 у сумі не дорівнюють 1,0 (або 100%). (Насправді їх сума дорівнює 1,43.) Метод "один проти всіх" визначає імовірність для кожного з двійкових наборів результатів незалежно від інших. Тобто ми визначаємо ймовірність того, що зображення є яблуком ("так" або "ні"), не враховуючи вірогідність інших варіантів фруктів, таких як апельсин, груша чи виноград.

Але що як потрібно передбачити ймовірність кожного варіанта фрукта в порівнянні з іншими? Тоді замість того, щоб прогнозувати, чи це яблуко ("так" чи "ні"), слід визначати вірогідність цього проти ймовірності апельсина, груші й винограду. Цей тип багатокласової класифікації називається один проти одного.

Класифікацію "один проти одного" можна реалізувати, використовуючи той самий тип архітектури нейронної мережі, як і для методу "один проти всіх", з однією ключовою зміною. Потрібно застосовувати іншу трансформацію до вихідного шару.

Для рішення "один проти всіх" ми застосували сигмоїдну функцію активації окремо до кожного вихідного вузла. Як результат, вихідні значення кожного вузла були між 0 і 1, але їх сума не завжди дорівнювала 1.

Натомість для рішення "один проти одного" можна застосувати функцію softmax, яка призначає десяткові значення ймовірності кожному класу задачі з кількома класами, щоб усі вони в сумі становили 1,0. Це додаткове обмеження допомагає швидше досягти збіжності при навчанні, ніж в інших випадках.

Натисніть значок плюса, щоб побачити рівняння softmax.

Формула softmax виглядає так:

$$p(y = j|\textbf{x}) = \frac{e^{(\textbf{w}_j^{T}\textbf{x} + b_j)}}{\sum_{k\in K} {e^{(\textbf{w}_k^{T}\textbf{x} + b_k)}} }$$

Зауважте, що вона по суті дає змогу використовувати формулу логістичної регресії для кількох класів.

На зображенні нижче показано, як завдання з багатокласової класифікації "один проти всіх" реалізується методом "один проти одного". Зауважте, що для виконання функції softmax в прихованому шарі, який безпосередньо передує вихідному шару (шарі softmax), має бути така сама кількість вузлів, як і у вихідному шарі.

Рисунок 9. Реалізація класифікації "один проти одного" на основі нейромережі з використанням шару softmax. Кожне вихідне значення – це ймовірність того, що вхідне зображення є вказаним фруктом, а не одним із трьох інших (сума всіх значень вірогідності дорівнює 1,0). Ця модель прогнозує, що ймовірність того, що зображення є грушею, становить 63%.

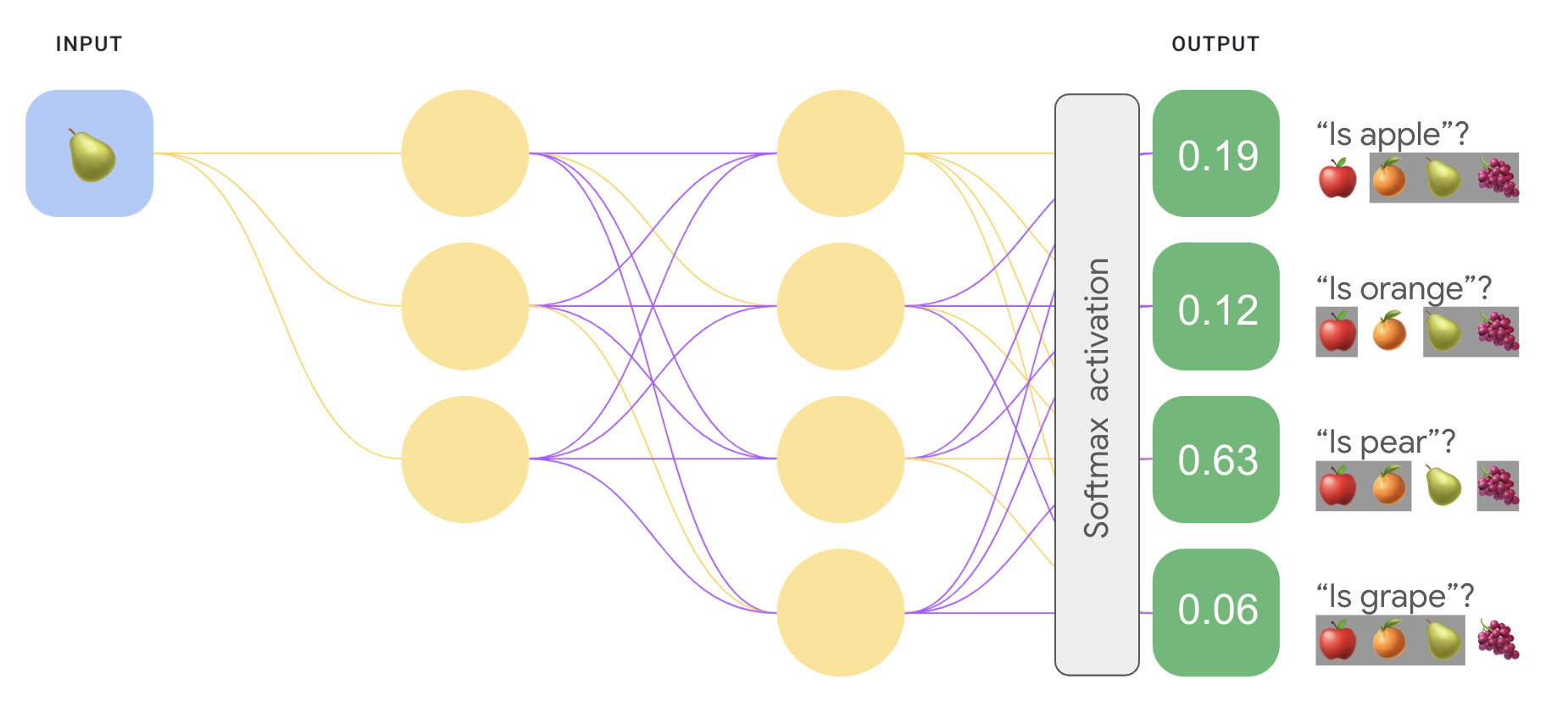
Варіанти функції softmax

Розгляньмо варіанти функції softmax, наведені нижче.

• Повна функція softmax – це та функція softmax, яку ми обговорювали, тобто яка обчислює імовірність для кожного можливого класу.

• Вибірка кандидатів означає, що функція softmax обчислює імовірність для всіх позитивних міток і лише для випадкової вибірки негативних міток. Наприклад, якщо потрібно визначити, це бігль на вхідному зображенні чи бладгаунд, значення ймовірності для кожного прикладу, який не є собакою, не знадобляться.

Повна функція softmax є досить дешевим варіантом, якщо класів небагато, але стає непомірно дорогою, коли кількість класів зростає. Вибірка кандидатів може підвищити ефективність для задач із великою кількістю класів.

Одна мітка проти багатьох міток

Функція softmax передбачає, що кожен приклад належить точно до одного класу. Однак деякі приклади можуть належати одночасно до кількох класів. У такому разі:

• не можна використовувати функцію softmax;
• слід покладатися на численні логістичні регресії.

Наприклад, модель "один проти одного" з рисунка 9, наведеного вище, передбачає, що кожне вхідне зображення міститиме рівно один тип фруктів: яблуко, апельсин, грушу або виноград. Однак якщо на вхідному зображенні не один тип фруктів (наприклад, миска яблук і апельсинів), доведеться використовувати кілька логістичних регресій.

Ключові терміни

• Двійкова класифікація
• Багатокласова класифікація
• Класифікація "один проти всіх"
• Softmax (класифікація "один проти одного")