En el ejercicio anterior, viste que agregar capas ocultas a la red no era suficiente para representar no linealidades. Las operaciones lineales que se realizan en operaciones lineales siguen siendo lineales.
¿Cómo puedes configurar una red neuronal para que aprenda relaciones no lineales entre valores? Necesitamos una forma de insertar operaciones matemáticas no lineales en un modelo.
Si esto te resulta familiar, es porque ya aplicamos operaciones matemáticas no lineales a la salida de un modelo lineal antes en el curso. En el módulo de Regresión logística, adaptamos un modelo de regresión lineal para generar un valor continuo de 0 a 1 (que representa una probabilidad) pasando la salida del modelo a través de una función sigmoidea.
Podemos aplicar el mismo principio a nuestra red neuronal. Revisemos nuestro modelo del Ejercicio 2 anterior, pero esta vez, antes de mostrar el valor de cada nodo, primero aplicaremos la función sigmoidea:
Intenta realizar los cálculos de cada nodo. Para ello, haz clic en el botón >| (a la derecha del botón de reproducción). Revisa las operaciones matemáticas realizadas para calcular el valor de cada nodo en el panel Cálculos debajo del gráfico. Ten en cuenta que el resultado de cada nodo ahora es una transformación sigmoidea de la combinación lineal de los nodos de la capa anterior, y los valores de salida están todos comprimidos entre 0 y 1.
Aquí, la función sigmoidea funciona como una función de activación para la red neuronal, una transformación no lineal del valor de salida de una neurona antes de que el valor se pase como entrada a los cálculos de la siguiente capa de la red neuronal.
Ahora que agregamos una función de activación, agregar capas tiene un mayor impacto. Apilamiento de no linealidad en no linealidad nos permite modelar relaciones muy complicadas entre las entradas y las salidas previstas. En resumen, cada capa aprende de manera eficaz una función más compleja y de nivel superior sobre las entradas sin procesar. Si quieres intuir mejor cómo funciona esto, consulta la excelente entrada de blog de Chris Olah.
Funciones de activación comunes
Tres funciones matemáticas que se usan comúnmente como funciones de activación son la sigmoidea, la tanh y la ReLU.
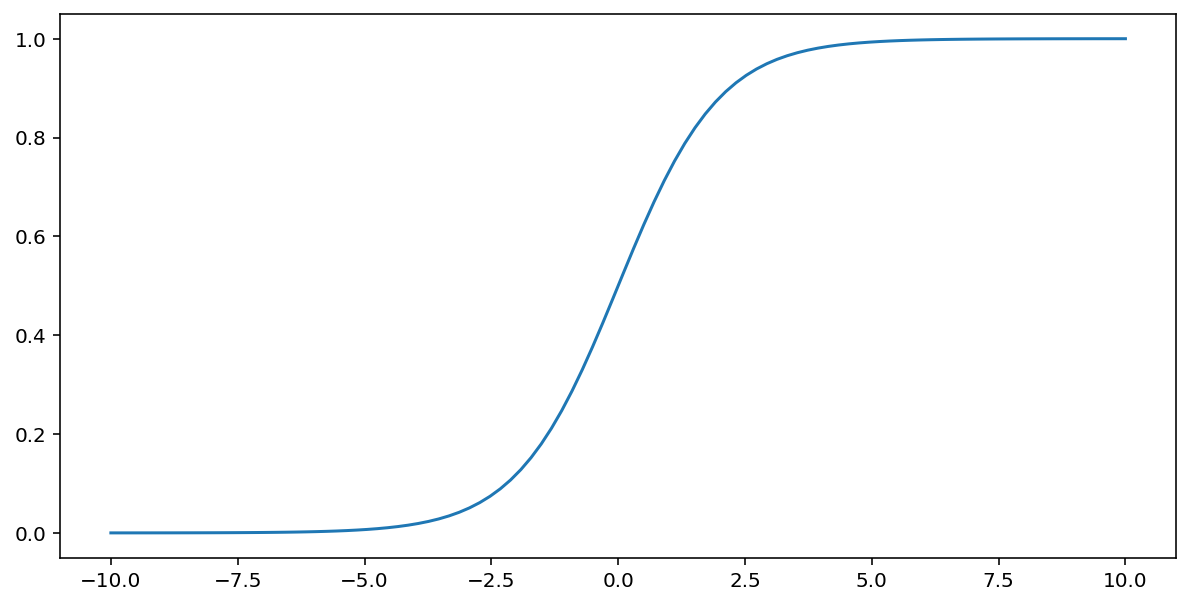
La función sigmoidea (que se analizó anteriormente) realiza la siguiente transformación en la entrada $x$, lo que genera un valor de salida entre 0 y 1:
\[F(x)=\frac{1} {1+e^{-x}}\]
Aquí hay un gráfico de esta función:
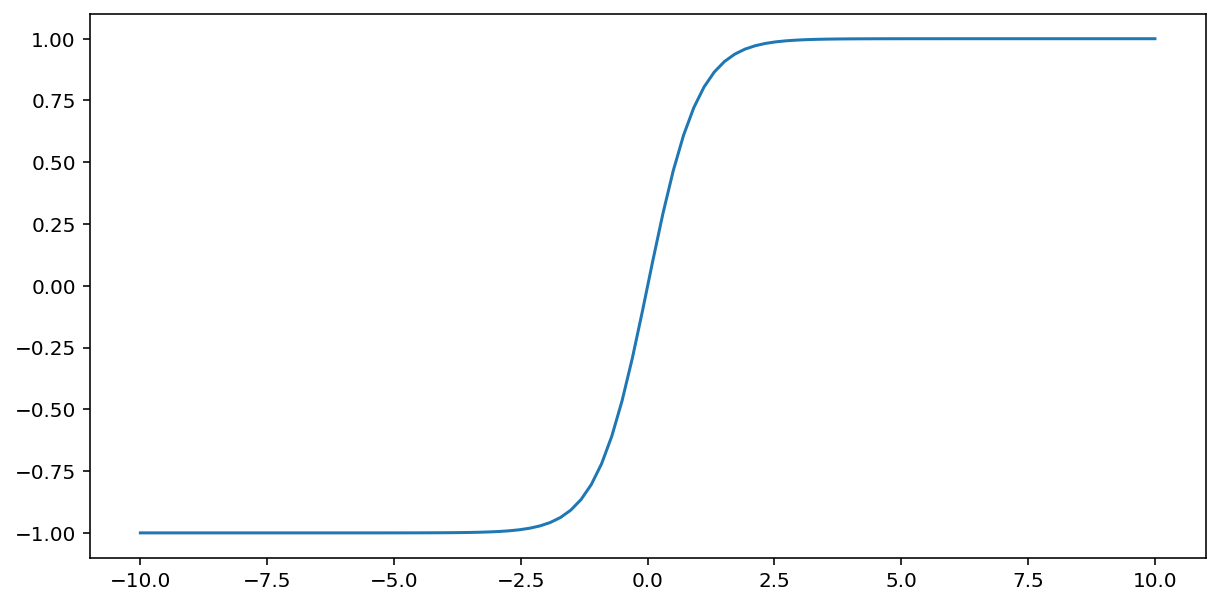
La función tanh (abreviatura de “tangente hiperbólica”) transforma la entrada $x$ para producir un valor de salida entre -1 y 1:
\[F(x)=tanh(x)\]
Esta es una gráfica de esta función:
La función de activación de la unidad lineal rectificada (o ReLU, en resumen) transforma el resultado con el siguiente algoritmo:
- Si el valor de entrada $x$ es menor que 0, muestra 0.
- Si el valor de entrada $x$ es mayor o igual que 0, muestra el valor de entrada.
La ReLU se puede representar matemáticamente con la función max():
Esta es una gráfica de esta función:
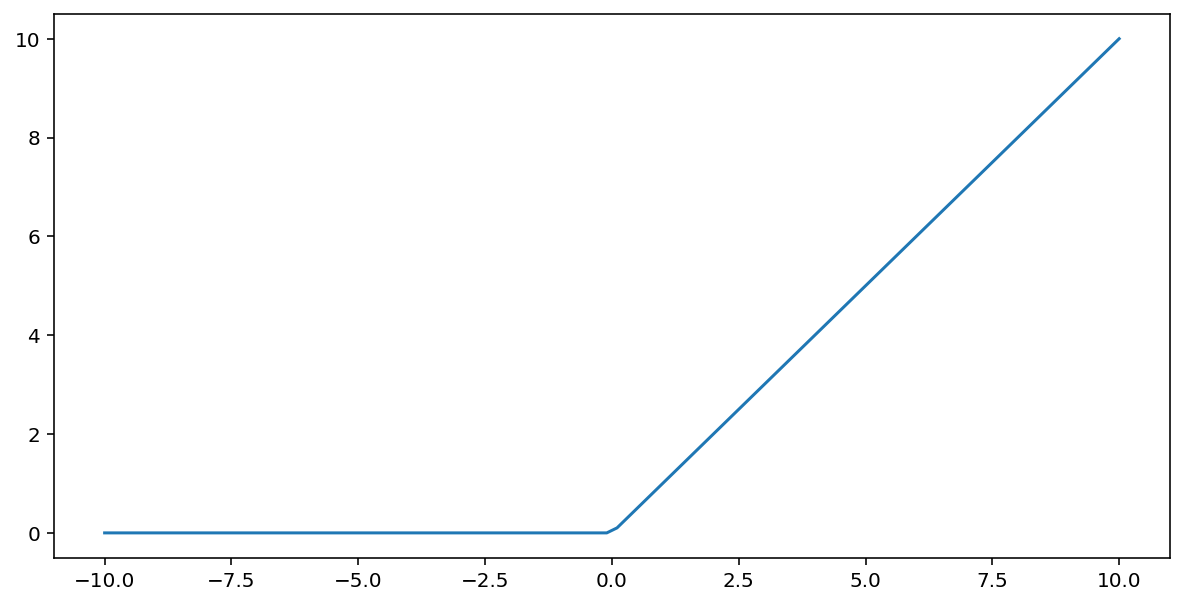
A menudo, la ReLU funciona mejor como función de activación que una función suave, como la sigmoidea o tanh, porque es menos susceptible al problema de gradiente de fuga durante el entrenamiento de la red neuronal. ReLU también es mucho más fácil de procesar que estas funciones.
Otras funciones de activación
En la práctica, cualquier función matemática puede servir como función de activación. Supongamos que \(\sigma\) representa nuestra función de activación. El valor de un nodo en la red se obtiene con la siguiente fórmula:
Keras proporciona compatibilidad inmediata con muchas funciones de activación. Aun así, recomendamos comenzar a trabajar con ReLU.
Resumen
En el siguiente video, se proporciona un resumen de todo lo que aprendiste hasta ahora sobre cómo se construyen las redes neuronales:
Ahora, nuestro modelo tiene todos los componentes estándar de lo que las personas suelen mencionar cuando se refieren a una red neuronal:
- Un conjunto de nodos, análogos a las neuronas, organizados en capas.
- Un conjunto de pesos que representan las conexiones entre cada capa de la red neuronal y la capa inferior. La capa inferior puede ser otra capa de la red neuronal u otro tipo de capa.
- Un conjunto de sesgos, uno para cada nodo.
- Una función de activación que transforma el resultado de cada nodo en una capa. Las diferentes capas pueden tener diferentes funciones de activación.
Una salvedad: las redes neuronales no siempre son mejores que las combinaciones de atributos, pero ofrecen una alternativa flexible que funciona bien en muchos casos.
