لقد تبيّن لك في التمرين السابق أنّ مجرد إضافة طبقات مخفية إلى شبكتنا لم يكن كافيًا لتمثيل الوظائف غير الخطية. إنّ العمليات الخطية التي يتم إجراؤها على العمليات الخطية تظلّ خطية.
كيف يمكنك ضبط شبكة عصبية للتعرّف على العلاقات غير الخطية بين القيم؟ نحتاج إلى طريقة لإدراج عمليات حسابية غير خطية في نموذج.
إذا كان هذا يبدو مألوفًا إلى حد ما، يرجع ذلك إلى أنّنا طبّقنا عمليات رياضية غير خطية على ناتج نموذج خطي في وقت سابق من الدورة التدريبية. في وحدة الانحدار اللوجستي، عدّلنا نموذج الانحدار الخطي لعرض قيمة مستمرة من 0 إلى 1 (تمثّل احتمالية) من خلال تمرير ناتج النموذج من خلال دالة سينوية.
يمكننا تطبيق المبدأ نفسه على شبكتنا العصبية. لنطّلِع مجددًا على النموذج الذي أنشأناه في التمرين 2 سابقًا، ولكن هذه المرة، قبل عرض قيمة كل عقدة، سنطبّق أولاً الدالة السينية:
جرِّب التنقّل في عمليات حساب كل عقدة من خلال النقر على الزر >| (على يسار زر التشغيل). راجِع العمليات الحسابية التي تمّ إجراؤها لحساب قيمة كلّ عقدة في لوحة العمليات الحسابية أسفل الرسم البياني. يُرجى العِلم أنّ ناتج كل عقدة هو الآن تحويل لوغاريتمي خطي لجمع العقد في الطبقة السابقة، وتكون قيم المخرجات كلها مضغوطة بين 0 و1.
في هذه الحالة، تعمل الدالة السينية على نحوٍ مشابه ل دالة التفعيل للشبكة العصبية، وهي عملية تحويل غير خطية لقيمة ناتج خلية عصبية قبل تمرير القيمة كإدخال إلى عمليات حساب الخطوة التالية للشبكة العصبية.
بعد أن أضفنا دالة تنشيط، أصبحت إضافة الطبقات أكثر تأثيرًا. إنّ تجميع الوظائف غير الخطية مع بعضها يتيح لنا نمذجة علاقات معقدة للغاية بين المدخلات والنواتج المتوقّعة. باختصار، تتعلّم كل طبقة بفعالية دالة أكثر تعقيدًا ومستوى أعلى من الإدخالات التلقائية. إذا كنت ترغب في اكتساب معرفة حول كيفية عمل ذلك، يمكنك الاطّلاع على مشاركة المدونة الممتازة التي نشرها "كريس أولا".
دوالّ التفعيل الشائعة
هناك ثلاث دوال رياضية تُستخدَم عادةً كدوالّ تنشيط، وهي دالة الصعداء والدالة tanh ودالة ReLU.
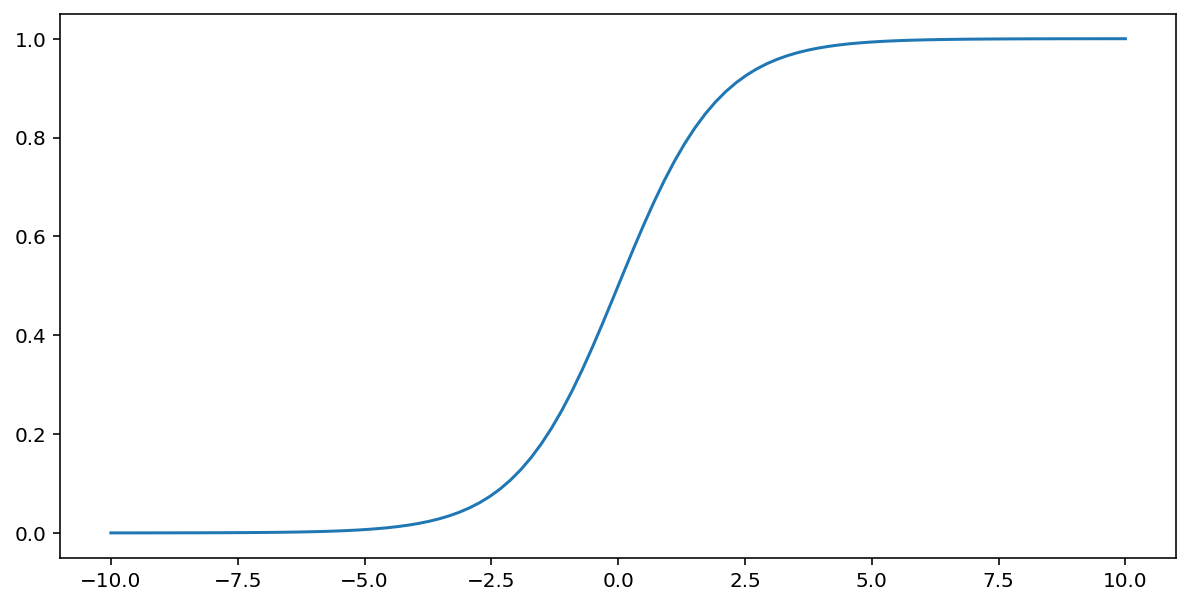
تُجري الدالة السينية (المُناقشة أعلاه) عملية التحويل التالية على الإدخال $x$، ما يؤدي إلى إنشاء قيمة ناتجة تتراوح بين 0 و1:
\[F(x)=\frac{1} {1+e^{-x}}\]
في ما يلي رسم بياني لهذه الدالة:
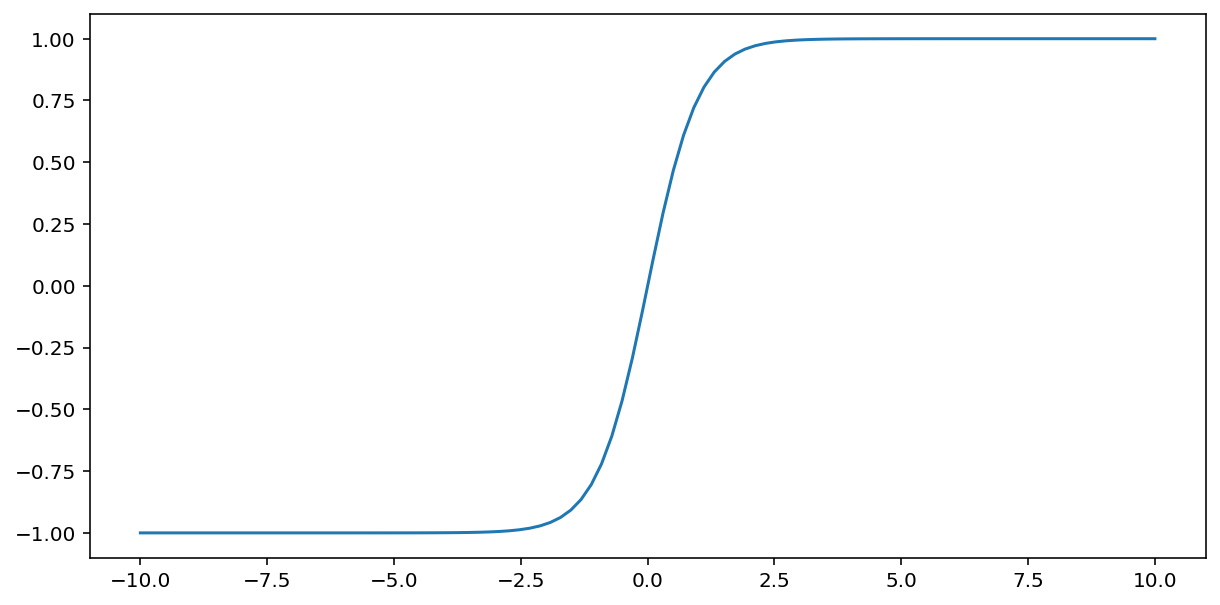
تعمل الدالة tanh (اختصارًا لـ "ظل التمام الزائدي") على تحويل الإدخال x لمحاولة توليد قيمة ناتجة تتراوح بين -1 و1:
\[F(x)=tanh(x)\]
في ما يلي رسم بياني لهذه الدالة:
تحوِّل دالة التفعيل الوحدة الخطية المعدَّلة (أو ReLU اختصارًا) الإخراج باستخدام الخوارزمية التالية:
- إذا كانت قيمة الإدخال $x$ أقل من 0، يتم عرض القيمة 0.
- إذا كانت قيمة الإدخال $x$ أكبر من أو تساوي 0، اعرض قيمة الإدخال.
يمكن تمثيل ReLU رياضيًا باستخدام الدالة max():
في ما يلي رسم بياني لهذه الدالة:
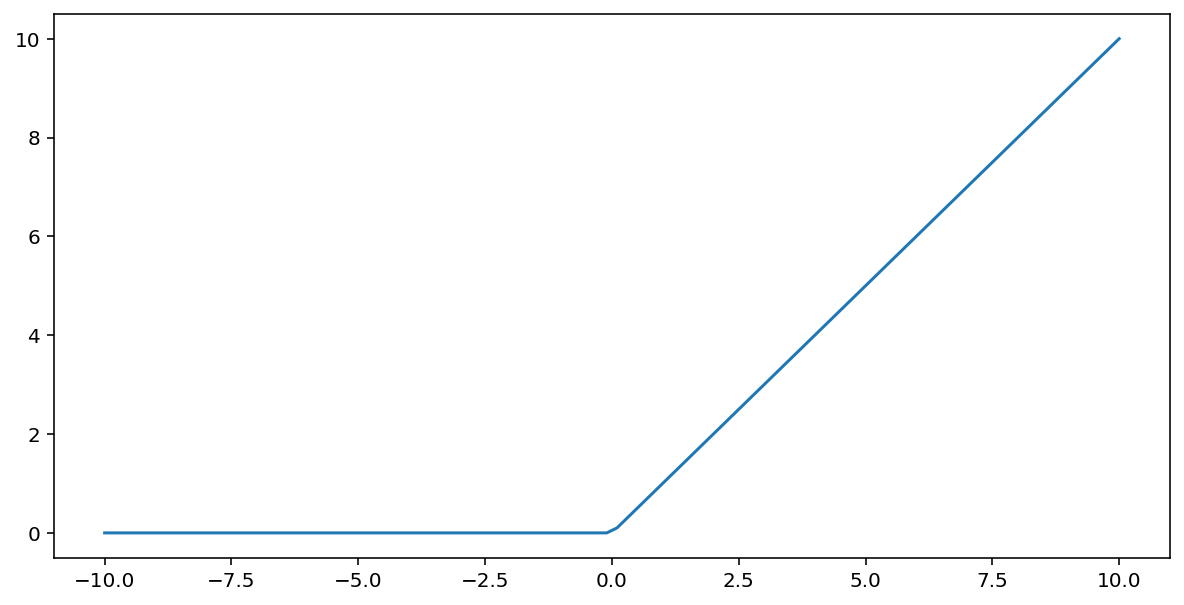
غالبًا ما تعمل دالة ReLU بشكل أفضل قليلاً كدالة تنشيط مقارنةً بالدالة السلسة مثل الدالة السينية أو tanh، لأنّها أقل عرضةً لمشكلة تلاشي التدرّج أثناء تدريب الشبكة العصبية. كما أن حساب ReLU أسهل بشكل كبير من هذه الدوال.
دوال التفعيل الأخرى
من الناحية العملية، يمكن أن تكون أي دالة رياضية بمثابة دالة تفعيل. لنفترض أنّ \(\sigma\) تمثل دالة التفعيل. يتم تحديد قيمة عقدة في الشبكة باستخدام العبارة التالية:
توفّر Keras دعمًا مُعدًّا مسبقًا للعديد من وظائف التفعيل. مع ذلك، ما زلنا ننصح بالبدء باستخدام ReLU.
ملخّص
يقدم الفيديو التالي ملخصًا لكل ما تعلمته حتى الآن حول كيفية إنشاء الشبكات العصبية:
الآن يحتوي نموذجنا على جميع المكونات القياسية لما يعنيه الأشخاص عادةً عندما يشيرون إلى الشبكة العصبية:
- مجموعة من العُقد، مماثلة للخلايا العصبية، مرتبة في طبقات.
- مجموعة من الأوزان التي تمثّل الاتصالات بين كلّ خطوة في الشبكة العصبية والخطوة التي تليها وقد تكون الطبقة تحتها طبقة شبكة عصبية أخرى أو نوعًا آخر من الطبقات.
- مجموعة من الانحيازات، واحدة لكل عقدة
- دالة تنشيط تحوّل ناتج كل عقدة في طبقة قد تحتوي الطبقات المختلفة على دوالّ تنشيط مختلفة.
تنبيه: الشبكات العصبية ليست بالضرورة أفضل من علامات التقاطعات، لكن الشبكات العصبية توفر بديلاً مرنًا يعمل بشكل جيد في كثير من الحالات.
