Comme vous l'avez vu dans l'exercice précédent, il suffit d'ajouter des couches cachées à notre réseau ne suffisait pas à représenter les non-linéarités. Les opérations linéaires effectuées sur des opérations linéaires restent linéaires.
Comment configurer un réseau de neurones pour apprendre des relations non linéaires entre les valeurs ? Nous avons besoin d'un moyen d'insérer des des opérations mathématiques dans un modèle.
Si cela vous semble familier, c'est parce que nous avons appliqué des opérations mathématiques non linéaires à la sortie d'un modèle linéaire tout au long du cours. Dans la régression logistique, nous avons adapté un modèle de régression linéaire pour obtenir une valeur continue de 0. à 1 (représentant une probabilité) en transmettant la sortie du modèle via une Fonction sigmoïde.
Nous pouvons appliquer le même principe à notre réseau de neurones. Reprenons notre modèle de l'exercice 2 plus tôt, mais cette fois, Pour générer la valeur de chaque nœud, nous allons d'abord appliquer la fonction sigmoïde:
Essayez de parcourir les calculs de chaque nœud en cliquant sur le bouton >| (à droite du bouton de lecture). Examiner les opérations mathématiques effectuées pour calculer la valeur de chaque nœud dans le panneau Calculs situé sous le graphique. Notez que la sortie de chaque nœud est maintenant une transformation sigmoïde de la combinaison de nœuds de la couche précédente, et les valeurs de sortie sont sont écrasées entre 0 et 1.
Ici, la fonction sigmoïde sert fonction d'activation pour le réseau de neurones, une transformation non linéaire de la valeur de sortie d'un neurone avant que la valeur ne soit transmise en tant qu'entrée aux calculs de la du réseau de neurones.
Maintenant que nous avons ajouté une fonction d'activation, l'ajout de couches a plus d'impact. L'empilement de non-linéarités sur des non-linéarités permet de modéliser des les relations entre les entrées et les sorties prédites. En bref, chaque couche consiste à apprendre une fonction plus complexe et de niveau supérieur par rapport à l'ensemble d'entrée. Si vous souhaitez développer plus intuition sur la façon dont cela fonctionne, consultez l'excellent article de blog publié par Chris Olah.
Fonctions d'activation courantes
Trois fonctions mathématiques couramment utilisées comme fonctions d'activation sont les suivantes : sigmoïde, tanh et ReLU.
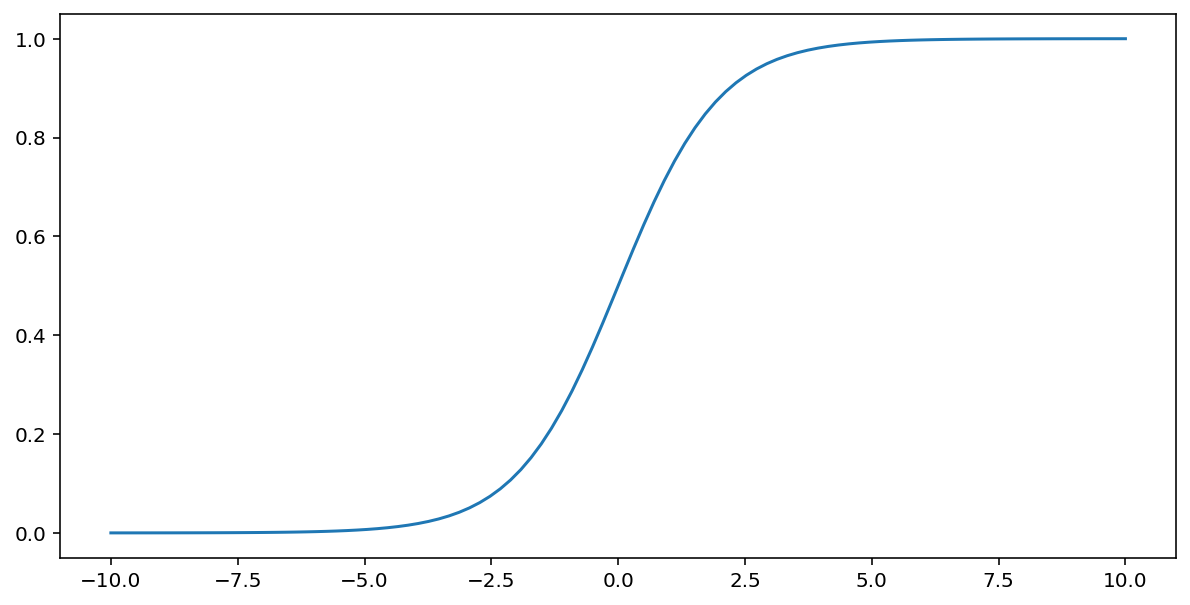
La fonction sigmoïde (décrite ci-dessus) effectue la transformation suivante en entrée $x$, produisant une valeur de sortie comprise entre 0 et 1:
\[F(x)=\frac{1} {1+e^{-x}}\]
Voici un graphique illustrant cette fonction:
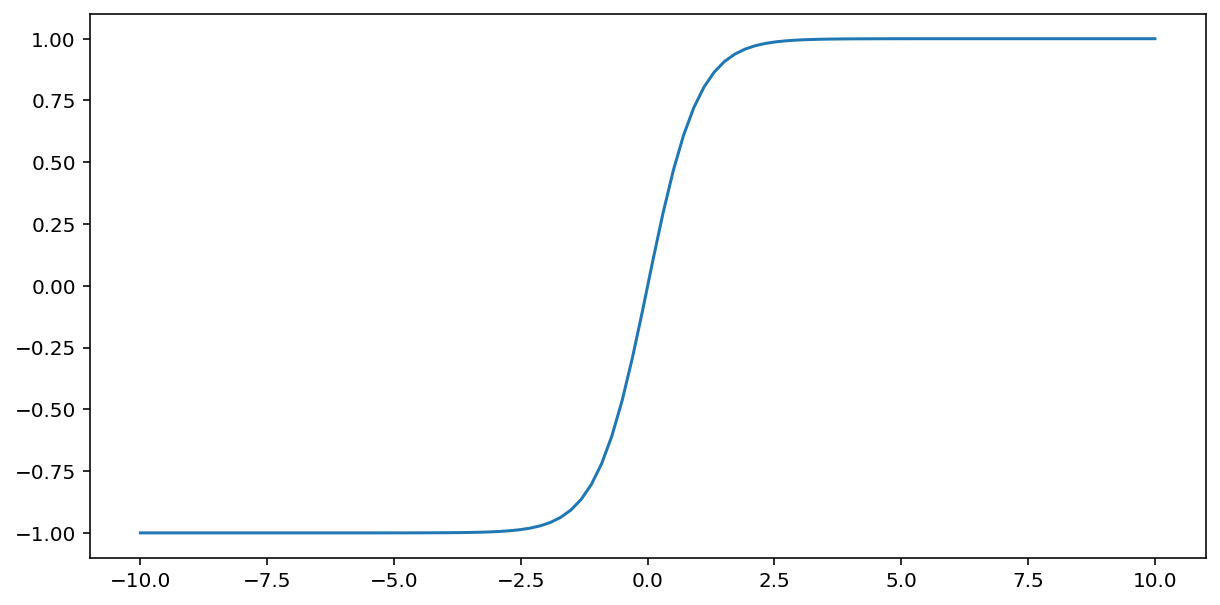
<ph type="x-smartling-placeholder">La fonction tanh (abréviation de "tangente hyperbolique") transforme l'entrée $x$ en génèrent une valeur de sortie comprise entre -1 et 1:
\[F(x)=tanh(x)\]
Voici un graphique illustrant cette fonction:
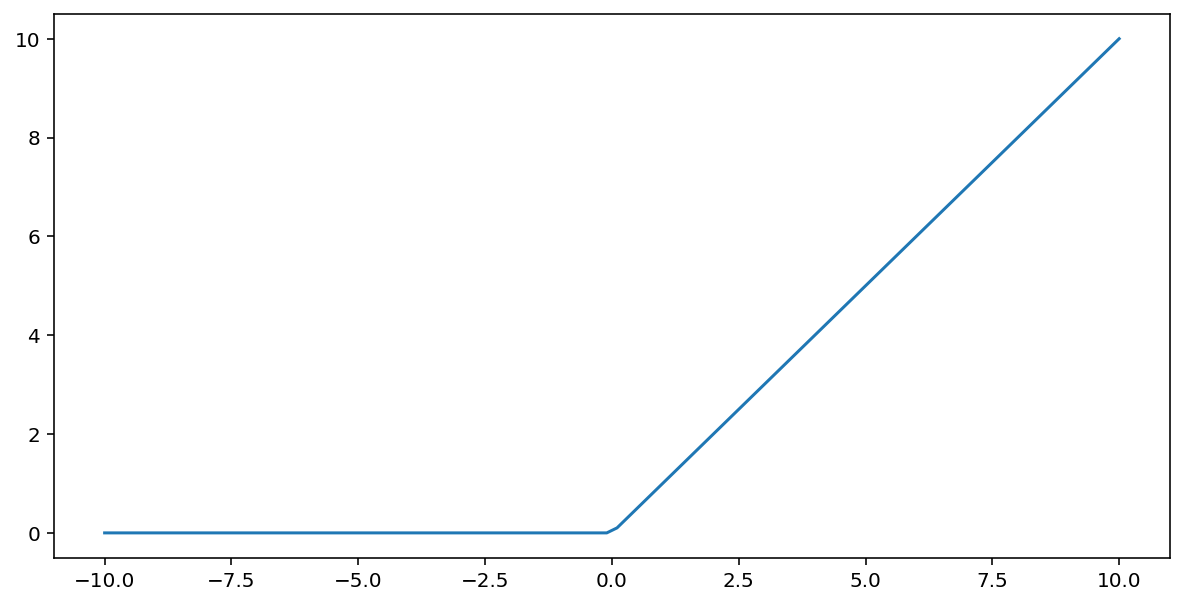
<ph type="x-smartling-placeholder">La fonction d'activation de l'unité de rectification linéaire (ou ReLU, pour (court) à l'aide de l'algorithme suivant:
- Si la valeur d'entrée $x$ est inférieure à 0, renvoie 0.
- Si la valeur d'entrée $x$ est supérieure ou égale à 0, renvoie la valeur d'entrée.
La fonction ReLU peut être représentée mathématiquement par la fonction max() :
Voici un graphique illustrant cette fonction:
<ph type="x-smartling-placeholder">La fonction ReLU est souvent un peu plus efficace en tant que fonction d'activation qu'en tant que fonction d'entraînement comme la fonction sigmoïde ou tanh, car elle est moins sensible au problème de disparition du gradient lors de l'entraînement sur les réseaux de neurones. La fonction ReLU est aussi beaucoup plus facile que ces fonctions.
Autres fonctions d'activation
En pratique, toute fonction mathématique peut servir de fonction d'activation. Supposons que \(\sigma\) représente notre fonction d'activation. La valeur d'un nœud du réseau est donnée par formule:
Keras fournit une assistance prête à l'emploi pour de nombreux fonctions d'activation. Toutefois, nous vous recommandons quand même de commencer par la fonction ReLU.
Résumé
La vidéo suivante récapitule tout ce que vous avez appris jusqu'à présent sur la construction des réseaux de neurones:
Notre modèle contient à présent tous les composants standards de ce que les gens quand ils font référence à un réseau de neurones:
- Un ensemble de nœuds, semblables à des neurones, organisés en couches.
- Un ensemble de pondérations représentant les connexions entre chaque réseau de neurones calque et la couche inférieure. La couche sous-jacente peut être d'une autre couche de réseau de neurones ou d'un autre type de couche.
- Un ensemble de biais, un pour chaque nœud.
- Fonction d'activation qui transforme la sortie de chaque nœud d'une couche. Différentes couches peuvent avoir des fonctions d'activation différentes.
Attention: les réseaux de neurones ne sont pas toujours meilleurs que les croisements de caractéristiques, mais les réseaux de neurones offrent une alternative flexible qui fonctionne dans de nombreux cas.